1. 그래프의 수학적인 표현
그래프는 “정점 집합과 간선 집합으로 이루어진 수학적 구조”라고 정의했으므로
정점의 집합을 V, 간선의 집합을 E라 하여 G=(V,E)로 표기

2. Neighbor
어떤 node의 neighbor은 그 node와 직접적으로 연결된 모든 node의 집합
V의 neighbor을 N(V)로 표기
자기 자신은 Neighbor라고 하진 않아

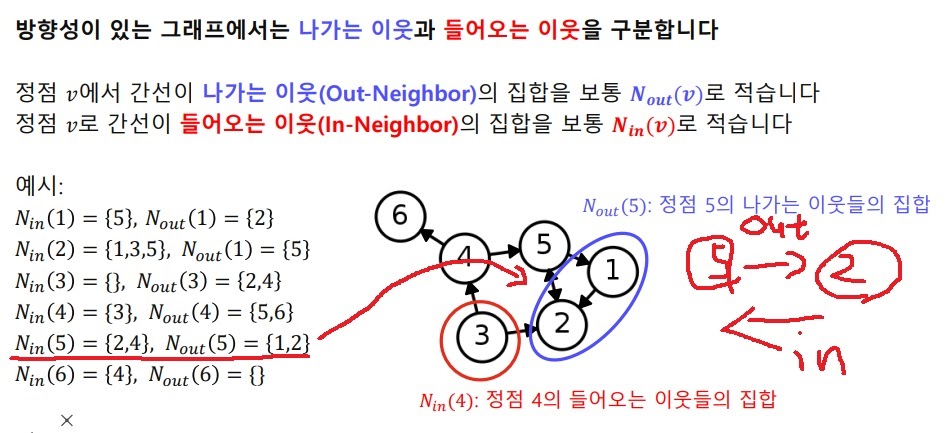
3. directed graph
directed graph에서는 나가는 neighbor와 들어오는 neighbor을 구분한다.
어떤 node V에서 link가 나가는 방향으로 연결된 node는 V의 outcoming neighbor라 하고 $N_{out}(V)$로 표기
link가 node V로 들어오는 방향으로 연결된 node는 V의 incoming neighbor라 하고 $N_{in}(V)$로 표기
4. edge list
그래프에서 두 node i와 j를 link하면 (i,j)라는 list로 반환되는데 방향성이 있어서 j에서 i로 link하면 (j,i)라는 list로 반환
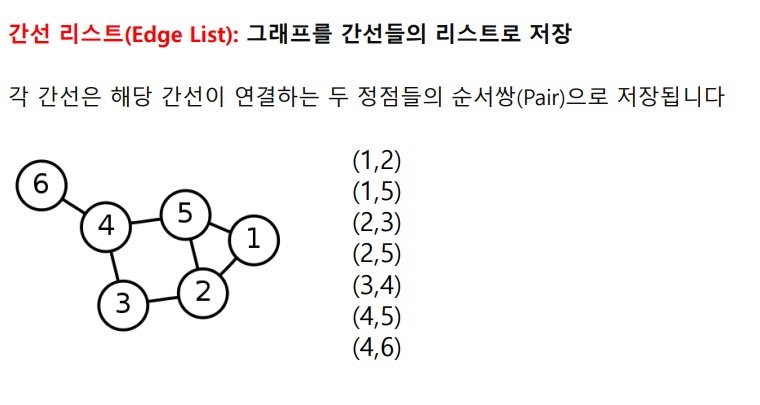
연산에 있어서 비효율적이다.
예를 들어 3에서 2로 연결되는 link를 찾고자 하는 경우 중간에 존재해서 확인이 되는데
2에서 3으로 연결되는 link를 찾고자하면 존재하지 않는다는 사실을 끝까지 탐색해봐야 안다는 점이다.

2에서 3으로 연결되는 link가 있는지 알기위해 리스트의 link를 모두 탐색해야 없다는 사실을 파악할 수 있음
굳이 다 안찾아보고도 있는지 없는지 아는게 효율적이지
5. adjacent list
특정 node의 neighbor를 list로 저장함

아마 dictionary를 쓰지 않을까?
방향성이 있는 경우는 incoming neighbor과 outcoming neighbor을 모두 저장

연산에 있어서 효율적인 측면을 갖는다.
3에서 2로 연결되는 link를 3번 가서 바로 찾을 수 있고 2에서 3으로 연결되는 link를 2번 가서 바로 찾을 수 있다.
6. adjacency matrix
i에서 j로 연결되는 link가 존재하면 (i,j)를 1로하고 없으면 0으로 한다
위 정의상 node 수 * node 수를 가지는 정방행렬
방향성이 없으면 i에서 j나 j에서 i나 대등하므로 대칭인 행렬이 된다.

방향성이 없는 그래프는 대칭인 행렬이 된다
방향성이 있으면 i에서 j나 j에서 i는 다르므로 대칭을 보장하지 않는다.

방향성이 있는 그래프는 대칭이 아니다
7. 일반행렬(general matrix)
그래프의 모든 원소를 그대로 저장하는 행렬
node 수의 제곱에 비례하는 저장 공간
8. 희소행렬(sparse matrix)
그래프에서 0이 아닌 것만 저장하는 행렬
link가 1인 것만 저장하니 link 수에 비례하는 저장 공간
대부분이 0인 경우는 저장공간을 아낄 수 있다.

그러나 대부분이 0이 아니면 오히려 일반행렬이 계산 속도가 빠르다고 한다.
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프의 path, distance, diameter 그리고 작은 세상 효과(small world effect) 이해하기 (0) | 2022.02.13 |
|---|---|
| 실제 그래프(real graph)와 랜덤 그래프(random graph) (0) | 2022.02.03 |
| 그래프(graph)의 유형 (0) | 2022.01.29 |
| 그래프(graph)와 관련된 인공지능 문제 (0) | 2022.01.27 |
| 그래프(graph)란 무엇인가? (0) | 2022.01.19 |

