1. directed graph
link에 방향성이 없고 두 node가 대등한 관계를 가질 수 있는 경우 undirected graph
link에 방향성이 있어서 두 node의 주체와 대상의 관계가 확실하고 의미있는 경우 directed graph
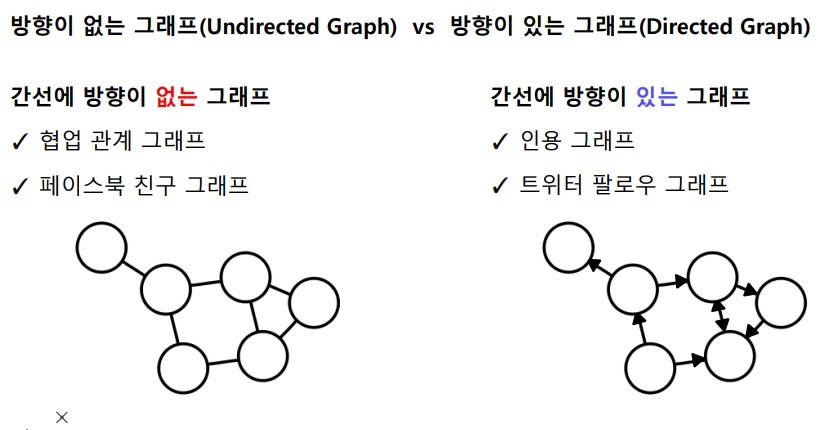
페이스북 친구는 서로 친구가 되어있어야 가능하므로 대등한 관계를 가져서 방향이 없는 그래프
인용 그래프의 경우 논문을 누가 인용했는지, 인용의 대상이 무엇인지 분명하므로 방향성이 있는 그래프
트위터 팔로우 그래프는 내가 태연을 트위터 팔로우 하더라도 태연은 나를 팔로우 하지 않잖아
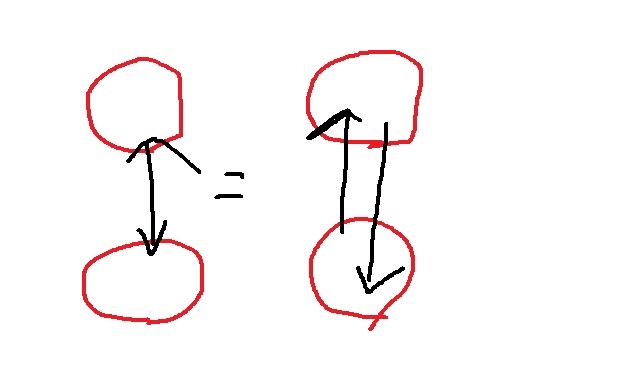
두 node사이에서 양쪽 방향으로 관계를 맺을 수도 있다.
물론 오른쪽 표기를 굳이 쓰진 않는다
사실 어느정도 주관적인 개념이다.
왜냐하면 주체와 대상의 관계가 있음에도 큰 의미가 없다면 undirected graph로 표현할 수도 있다.
2. weighted graph
때로는 어떤 link는 특별히 더 중요할 수도 있고 어떤 link는 별로 중요하지 않을 수도 있다.
이렇게 link에 특별한 중요 수치를 부여하여 다룰 수 있는 경우 weighted graph
그렇지 않은 경우 unweighted graph

마찬가지로 어느정도 주관적인 개념이다.
weight를 부여할 수 있어도 의미가 없는 경우 굳이 하지않고 unweighted로 표현
혹은 전화그래프의 경우 누구와 누가 전화했는지는 알아 link를 만들 수는 있는데
전화 몇번했는지 데이터가 없어서 weight를 부여할 수 없는 경우 unweighted로 표현
페이스북 친구 그래프의 경우 친구간 상호작용 정도를 추가해서 weighted로 표현할 수도 있다.
3. bipartite graph
node의 종류가 단일한 경우 unpartite graph로 표현하고 node의 종류가 2종류인경우 bipartite graph로 표현한다
bipartite graph의 경우 서로 다른 종류의 node끼리 link를 한다. 같은 종류의 node끼리는 link하지 않는다

전자 상거래 구매내역의 경우 사용자가 상품을 구매하지 사용자가 사용자를 구매하지 않고 상품이 상품을 구매하진 않는다
당연히 궁금한 것은 3종류 이상도 가능하지 않을까? tripartite graph라고 한다.
In graph theory, a part of mathematics, a k-partite graph is a graph whose vertices are or can be partitioned into k different independent sets. Equivalently, it is a graph that can be colored with k colors, so that no two endpoints of an edge have the same color.
같은 종류의 node끼리는 연결하지 않는 다는 사실을 위 정의에서도 알 수 있다
4. 다양한 방식으로 표현할 수 있는 그래프 유형

위와 같은 전자상거래 구매 내역은 가중치가 있으면서 방향성이 없는 bipartite graph로 표현했다.
그런데 전자상거래 구매내역을 표현하기 위해 위와 같이만 표현할 수 있는가? 그렇지 않다
예를 들어 방향성을 표현하여 방향성 그래프를 사용할 수도 있다.

그러나 사람이 물건을 구매하는 방향은 굳이 없어도 누구나 알 수 있으므로 의미가 없는 표현이다.
방향을 표현하여 그래프 복잡도가 커지는 것에 비해 의미있는 정보를 얻지 못하므로 굳이 방향성을 표현하진 않는다
마찬가지로 가중치를 굳이 표현해야하느냐?? 상황에 따라 표현할 필요가 없으면 표현하지 않아도 된다.
구매하고 싶은 정도?로 위와 같이 가중치를 표현했지만 그런 구매욕구 정도를 나타낼 필요가 없는 경우에는 안써도 되겠죠?
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프의 path, distance, diameter 그리고 작은 세상 효과(small world effect) 이해하기 (0) | 2022.02.13 |
|---|---|
| 실제 그래프(real graph)와 랜덤 그래프(random graph) (0) | 2022.02.03 |
| 그래프를 표현하는 수학적인 방법 (0) | 2022.01.31 |
| 그래프(graph)와 관련된 인공지능 문제 (0) | 2022.01.27 |
| 그래프(graph)란 무엇인가? (0) | 2022.01.19 |

