1. path
두 node u와 v사이 path란 다음 두 조건을 모두 만족하는 순열이다.
u에서 시작해서 v로 끝난다.
부분순열에서 연속된 두 node는 link되어 있다.
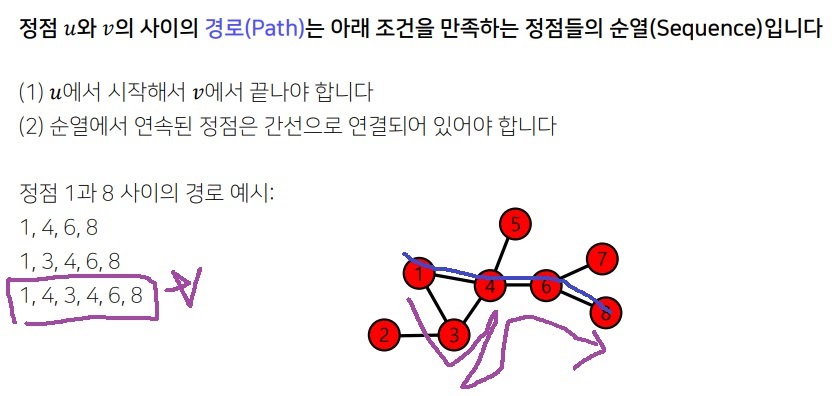
왕복하는 1,4,3,4,6,8도 1에서 8까지 path인데 1에서 시작해서 8로 끝나고 어느 두 연속된 node도 link되어 있어서 그렇다.

5에서 6은 끊어져있으니 1,3,4,5,6,8은 path가 아니다.
2. the length of path
해당 path에 존재하는 모든 link의 길이를 말한다.
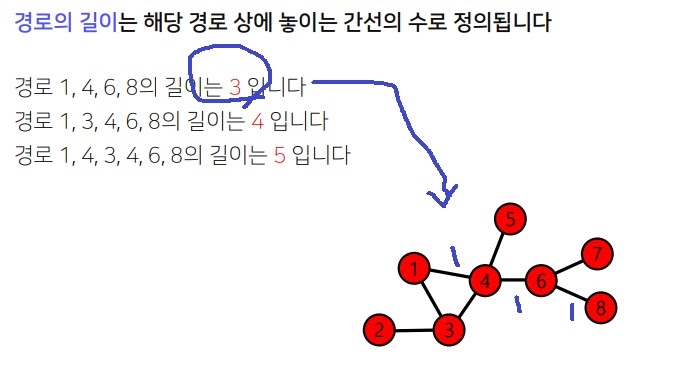
1,4,6,8에는 3개의 link가 존재하므로 길이는 3
물론 link 1개의 길이가 1일때 그렇다
3. distance
두 node u와 v사이 distance는 모든 path중 최단경로의 길이
u와 v사이 모든 path를 구해서 length를 구했을 때 최솟값을 말한다
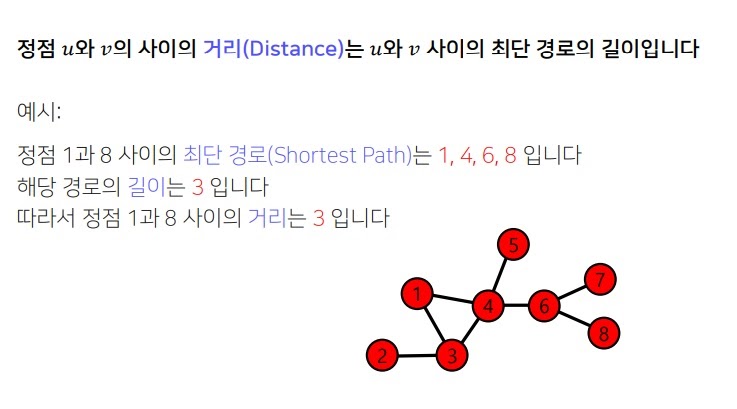
1에서 8까지 가는 모든 path중 가장 짧은 length의 path는 1,4,6,8이고 그 값이 3이므로 distance는 3
4. diameter
그래프에서 존재하는 임의의 두 node사이 distance를 모두 구해서 그것의 최댓값이 그래프의 diameter라고 한다.
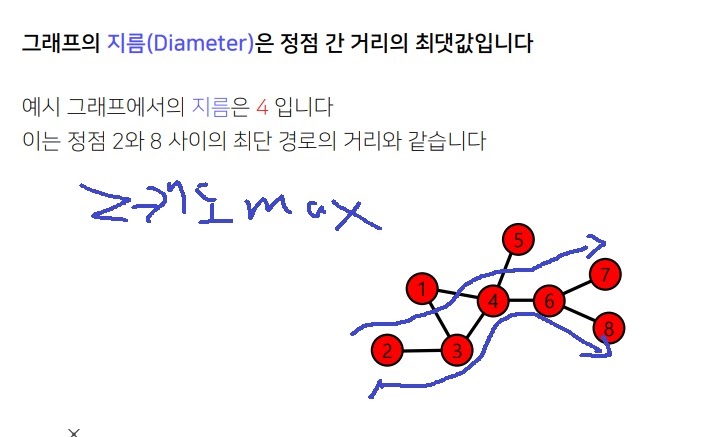
5. small world effect
real graph에서 임의로 2개의 node를 골랐을때 그 거리는 얼마정도 일까?
5-1) 여섯단계 분리 실험
“임의로 선택한 두 사람도 6단계만 거치면 연결할 수 있다”
오마하와 위치타에서 500명의 사람을 뽑아 보스턴의 한 사람에게 편지를 전달하고자하는 목적으로
본인들의 (보스턴에 지인이 있을 것 같은)지인에게 편지를 전달하라고 지시했다.
이 과정을 반복적으로 수행하였을 때 몇단계 지인을 거쳐야 보스턴까지 전달 될 수 있었을까?

오마하와 위치타는 보스턴과 거리가 멀기때문에 확률적으로 거기서 사는 사람들이 보스턴에 있는 사람을 직접적으로 알기는 어렵다.
근데 이 세팅이 설명하는 사람들마다 조금씩 다르다… 어떤 곳은 160명한테 물어봤다하고, 특정한 이름 가진 사람에게 전달하라하고
비협조적인 사람들도 많아서 25%편지만 도착했다고 한다.
결과는 평균적으로 6단계안에 도착했다고 한다.
SNS가 존재하지 않았던 1960년대 오래전 실험인데 생각보다 짧은 거리에 도달한다는 점이 놀라운 결과

실험결과는 평균적으로 6단계안에 보스턴까지 도달했다.
비슷한 실험을 데이터 수가 훨씬 많은 MSN 메신저에 적용한다면 평균적으로 특정 사람에게 7단계에 도달했다.

데이터 수가 많더라도 평균적인 거리는 6단계랑 큰 차이 없이 7단계만에 특정한 다른 사람에게 도달할 수 있다
small world effect는 사람들이 생각보다 소수의 공통된 지인을 통해 연결되어 있다는 사실을 보여준다
real graph의 임의의 두 node 사이 거리가 생각보다 작다
6. random graph로 이해하는 small world effect
하나의 random graph를 생각해보면 small world effect는 놀라운 결과는 아니다.
모든 사람이 100명의 지인이 있다고 가정해보자.
어떤 특정한 사람이 5단계동안 연결될수있는 사람 수는 최대 100억명이다.
중복된 지인에 의해 100억명보다는 작아지겠지만 높은 확률로 아주 많은 사람들과 5단계안에 연결될수 있다는 사실

1단계 1명의 사람이 100명과 연결되고 그 중 1명은 지인이 100명 있으니
2단계에서는 첫번째 사람은 100*100명과 연결될 수 있다.
이런식으로 반복하면 5단계에서는 첫번째 사람은 100*100*100*100*100명과 연결된다
그러나 모든 그래프에서 small world effect가 존재하는 것은 아니다.
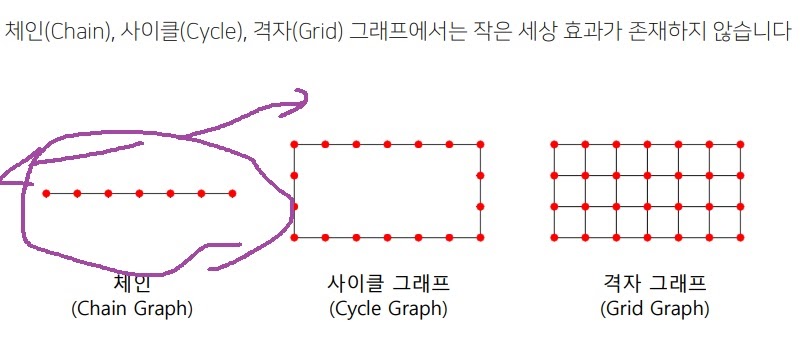
체인 그래프만 보더라도 크기가 커지면 임의의 두 node 사이 거리는 평균적으로 커질 것임
7. small world effect 추가적인 설명
Duncan Watts, Steven Strogatz라는 두 명의 학자가 "Nature"지에 기고한 논문에서 최초로 나타남.
1) 위키피디아에서는 small world network를 이렇게 정의하고 있다.
“small-world network란, 대부분의 node가 다른 node와 이웃이 아니나, 어떤 주어진 node의 이웃은 다른 node의 이웃일 가능성이 높고 대부분의 node는 적은 단계로 다른 node에 도달 할 수 있다”
2) 수학적으로는 임의의 두 node간 거리 L이 network의 노드 수 N의 로그에 비례하는 network이다. 그런 반면에 clustering coefficient는 작지 않다.
3) 사회과학 맥락에서 적은 지인으로도 모르는 사람과 연결되는 small world 현상이 일어나는 효과를 small world network가 말해준다.
4) 실생활에서 예시를 들어보면
뇌가 동작을 멈추는 것은 모든 뇌세포가 망가져서라기보다는 한 두개의 뇌세포가 망가져서 그런경우
감기 걸린 사람 1~2명만 있어도 network 전체에 감기를 퍼뜨리기는 쉽다
viral marketing도 하나의 예시다. 한 두명만 이런 저런 이야기하면 금방 이야기가 퍼지는경우 많이 보지 않았는가?
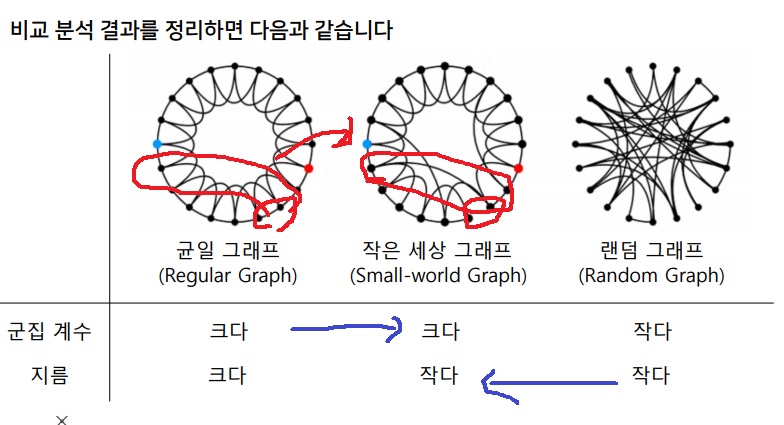
5) 모든 network는 그 연결방식에 따라 3가지로 나눌 수 있다.
5-1) 일정한 규칙에 따라 인접한 곳과 일정한 숫자로만 연결되는 ‘regular network’
이들은 link가 일정하게, 균일한 패턴으로 연결되어 clustering할 부분이 많아진다.
반면 하나의 node에서 다른 node로 가기 위해 항상 일정한 pattern으로 가기때문에 상대적으로 그 길이가 길다.
5-2) 무작위로 서로 연결된 ‘random network’
이들은 무작위로 연결되어 있어서 clustering하기가 어렵지만 임의의 두 node를 가기에는 평균적으로 짧은 거리에 갈 수 있다.
이 두 network의 중간쯤에서 구성원의 극히 일부만 엉뚱하게 연결된 ‘small world network’
network 자체가 엄청 크다고 하더라도 엉뚱하게 link된 소수의 구성요소때문에 network 전체가 서로 밀접한 관계에 놓일 수 있다는 것이 논문에서 말하는 small world effect이다.

영어가 길어서 무슨 소리인지 모르겠는데 핵심은 마지막이다.
p의 중간값을 선택했더니 그래프는 regular graph처럼 매우 높은 확률로 clustering 될 수 있고 그러나 random graph처럼 node간 거리가 작다는 것이다
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프의 연결성(degree)에 대한 고찰 (0) | 2022.02.16 |
|---|---|
| 그래프에서 중심성(centrality)의 척도들 (0) | 2022.02.16 |
| 실제 그래프(real graph)와 랜덤 그래프(random graph) (0) | 2022.02.03 |
| 그래프를 표현하는 수학적인 방법 (0) | 2022.01.31 |
| 그래프(graph)의 유형 (0) | 2022.01.29 |

