1. connected component
connected component란 다음 두 조건을 모두 만족하는 node의 집합
1) 모든 node가 path로 연결이 가능하다
2) 하나의 node를 추가 했을 때 위 조건을 만족해서는 안된다.

쉽게 생각해서 서로 연결되어 모여있는 집합들이 연결요소다.
{9} 하나의 경우도 위 network에서 하나의 연결요소다.
두번째 조건이 무슨 말인지 이해하기 어려운데
{1,2,3,4}의 경우 node 5를 추가하면 {1,2,3,4,5}는 첫번째 조건을 만족하므로 {1,2,3,4}는 연결요소가 아니라는 뜻이다.
2. giant connected component
In many networks as the network grows the components get gradually connected together.
At some point we can say that a significant proportion of the nodes are connected together in one Giant Component.
There is no strict definition of when a component becomes giant, so it really depends on the type of network.
We might simply say that a component becomes giant when a majority of nodes are connected (more than half).
그래프에서 대부분의 node를 포함하는 connected component가 giant connected component이다.
문제는 이 대부분의? 정의가 뭔지 궁금했는데 hub처럼 엄격하게 정의하진 않고 충분히 큰 수의 node를 포함하는 connected component를 말하는 듯 하다.
3. real graph
real graph의 경우 거의 대부분은 giant connected component가 존재할 것이다.
SNS 그래프만 생각해도 유명인의 팔로워 수는 엄청나서 거대한 연결요소를 만들어 낼 것
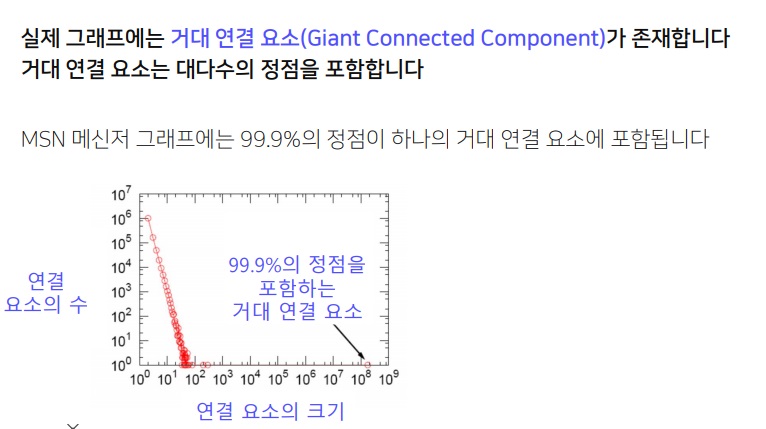
MSN 메시지에는 99.9%의 node를 포함하는 giant connected component를 생각할 수 있다고 한다.
4. Erdős–Rényi graph의 giant connected component
Erdős–Rényi random graph G(n,p)의 경우 giant connected component가 존재할 수 있다.
평균연결성 np가 1보다 크면 거의 확실하게 하나의 유일한 giant connected component가 존재한다고 알려져 있다.
If np < 1, then a graph in G(n, p) will almost surely have no connected components of size larger than O(log(n)).
If np = 1, then a graph in G(n, p) will almost surely have a largest component whose size is of order $n^{\frac{2}{3}}$
If np → c > 1, where c is a constant, then a graph in G(n, p) will almost surely have a unique giant component containing a positive fraction of the vertices.
No other component will contain more than O(log(n)) vertices.

직관적으로 받아들이기 힘들었는데 생각해보니 걍 평균연결성이 충분히 크면 당연한 결과긴 하다
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프를 다루는 파이썬의 NetworkX 라이브러리 맛보기 (0) | 2023.08.07 |
|---|---|
| 그래프의 군집구조(community) (0) | 2023.07.24 |
| 검색엔진의 역사를 바꾼 pagerank 알고리즘 파헤치기 (0) | 2022.10.23 |
| 그래프의 연결성(degree)에 대한 고찰 (0) | 2022.02.16 |
| 그래프에서 중심성(centrality)의 척도들 (0) | 2022.02.16 |

