1. layer의 계산적인 측면
self attention의 layer의 계산적인 측면에서 본다면 input sequence의 길이가 n이고 hidden vector의 차원이 d일때

Q는 n*d차원이고 $K^{T}$ 는 d*n차원이므로 $O(n^{2}d)$
RNN은 d차원의 $h_{t-1}$이 $h_{t}$로 변환되기위해서는 $W_{hh}$라는 d*d행렬을 곱하여 계산되는데 input sequence의 길이 n에 대하여 $O(nd^{2})$
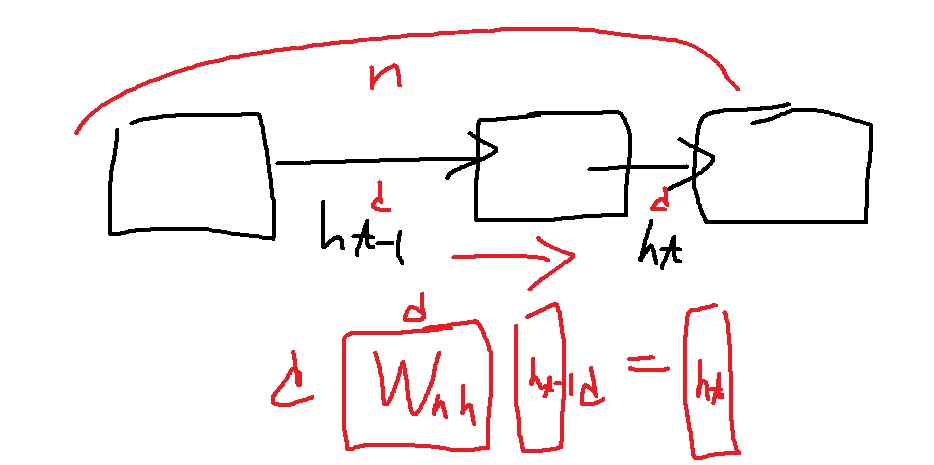
input sequence의 길이 n과 hidden vector의 차원 d는 의미적으로 큰 차이가 있는데 hidden vector의 차원은 hyperparameter로 선택할수있는 값이다.
그러나 input sequence는 선택할수 없는 값으로 데이터의 길이에 따라 다르다.
그래서 둘의 계산은 d보다는 input sequence인 n에 더욱 의존하게 된다.
self attention은 $O(n^{2})$에 가깝고 RNN은 $O(n)$에 더 가깝다는 의미임.
그래서 self attention이 layer의 계산적인 측면에서 메모리 요구량이 더 많다.
2. model의 sequential 측면
model의 sequential 측면에서 살펴보자. self attention은 input sequence의 길이와 무관하게 단 1번만 연산을 수행하면 된다는 장점이 있다.
RNN은 순서대로 입력을 받아 하나씩 쌓아가는 구조이기때문에 이전 계산이 완료되어야 다음 계산으로 넘어간다.
즉 input sequence의 길이 n에 의존한다. 그러니까 모델을 n번 돌려야한다는 소리임
self attention은 O(1)에 가깝고 RNN은 O(n)에 더 가깝다는 의미임.
이것은 무슨 말이냐? 전체적인 학습은 self attention이 빠르지만 메모리 사용량은 self attention이 많다.
3. maximum path length
maximum path length 관점에서 보자.
self attention은 q,k,v 변환으로 모든 input sequence를 처리하여 단 1번에 계산한다.
sequence의 길이와 무관하게 첫 단어랑 바로 연산이 가능함
self-attention은 이렇게 short term dependency의 문제를 해결했다.
그러나 RNN은 마지막 계산을 위해 첫 단어부터 sequence의 길이만큼 계산을 해야 할수있음
그래서 short term dependency 문제가 여전히 나타난다.

'딥러닝 > NLP' 카테고리의 다른 글
| transformer에 사용된 positional encoding에 대하여 (0) | 2022.05.13 |
|---|---|
| transformer에 사용된 residual connection과 layer normalization (0) | 2022.05.05 |
| multi-head attentiond 개념 알아보고 간단하게 구현해보기 (1) | 2022.05.02 |
| scaled dot product attention (1) | 2022.05.01 |
| 예시와 그림으로 이해하는 self attention의 원리 (0) | 2022.04.28 |

