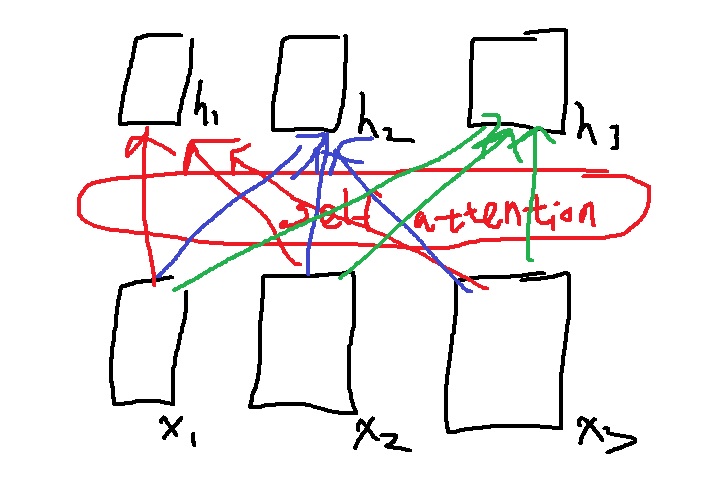
1. 예시로 알아보는 self attention

hidden state vector를 만들고자 하는 x1의 query를 q1으로 생성
1에서 x1의 query q1와 x1,x2,x3의 key k1,k2,k3 각각의 내적으로 score를 계산 (3.8,-0.2,5,9)
softmax를 취하여 어느 벡터에 집중할지 가중치를 계산 (0.2,0.1,0.7)
가중치인 score와 x1,x2,x3의 value v1,v2,v3의 weighted sum을 구한다.
즉 x1의 hidden vector h1=0.2v1+0.1v2+0.7v3으로 구해진다.
이러면 이제 x1,x2,x3를 학습이 가능한 weight matrix인 $W^{Q}, W^{K}, W^{V}$로 변환하여 얻은 query,key,value를 이용하였는데
query와 key의 내적을 구해서 자기 자신에 쓸데없이 집중하는 정도를 줄이고 다른 단어에 더욱 집중할 수 있도록 했다.
말 그대로 변환되었기 때문에 x1,x1 자기자신의 단순한 내적이 이제 큰 의미가 없지..
근데 여전히 자기 자신에 집중하는 정도가 제일 높을 수도 있다 경우에 따라 당연히,
그러나 이렇게 하는 것은 단순히 내적하는 것보다 합리적이다 이거임.
2. 행렬연산으로 알아보는 self attention
앞에서는 단순히 x1 하나의 벡터에만 집중해서 계산했는데 매 계산마다 x1, x2, x3 하나씩 계산하면 너무 오래 걸릴 것이다.
벡터들의 모임이 하나의 행렬인데 행렬계산을 이용해서 모든 input sequence에 대해 단 1번의 계산으로 attention을 수행하여 모든 hidden vector h1,h2,h3를 뽑아낼 수 있다.

위와 같이 두 단어 thinking, machine가 있다고 할때 embedding vector을 x1,x2라하자.
$W^{Q}, W^{K}, W^{V}$을 이용해서 두 단어 x1,x2를 query,key,value로 만든다.
두 벡터 x1,x2를 하나의 행렬 X로 concat을 한다. x1,x2를 각각 row vector로 가지는 X로 말이다.
이 행렬 X에 대해 $W^{Q}, W^{K}, W^{V}$를 이용한 선형변환을 수행하면
q1,q2를 row로 가지는 query matrix, k1,k2를 row로 가지는 key matrix, v1,v2를 row로 가지는 value matrix를 얻는다.

결과적으로 self attention은 단 1번의 연산으로 각각의 word가 다른 모든 word와의 연관성을 받은채로 encoding될 수 있다.
기존의 RNN은 다시한번 말하지만 The problem of short term dependency가 있었다.
먼 정보를 가져오기 위해 time step만큼 계속해서 정보를 압축해가며 전달해야했는데 그렇기 때문에 먼 정보일수록 정보의 손실이 일어났다는 것이다.
그러나 self attention은 sequence 길이가 아무리 길어도 query,key,value로 1번에 변환을 수행하여
단 1번에 모든 word끼리 연관성을 주고받은채로 attention 계산이 이루어지며 단 1번에 모든 벡터의 encoding vector를 뽑아낸다.
3. 수식으로 이해하는 self attention
query q와 key k의 내적 $q^{T}k$을 이용한 score를 계산하고
이 score에 softmax를 취한 것이 value의 가중치가 된다.
최종 output vector는 value의 weighted sum vector

여기서 1가지 중요한 점은 query와 key는 내적이 수행되어야하므로 차원이 같아야한다.
그러나 value는 이들과 무관하므로 차원이 달라도 상관없다. 그런데 편의상 보통 차원을 전부 같게 한다.(논문도 차원을 같게 했다.)

query와 key의 차원인 $d_{k}$는 뒤에서도 쓰이는 중요한 값이다.
query가 여러개인 경우, 그러니까 모든 input sequence에 대해 단 1번의 행렬 계산을 하는 경우
query matrix Q와 key matrix의 내적 $QK^{T}$의 $softmax(QK^{T})$에 value matrix를 곱하여 $softmax(QK^{T})V$로 구한다.

4. 그림으로 이해해보는 attention 행렬연산

$QK^{T}$연산을 수행하면 $q_{i}k_{j}$를 원소로 가지는 행렬이 생성된다.
이것의 softmax를 취하면 row wise 연산이 되어 각 행이 softmax weight vector가 된다. 첫 행이 (0.2,0.1,0.4,0.3)이라고 해보자.
이제 value와의 weighted sum을 하면 된다. 행렬끼리는 두 행렬을 곱하면 되는데
첫행만 계산해보면 0.2v1+0.1v2+0.4v3+0.3v4가 된다는 사실이 보인다.
word x1의 encoder vector가 0.2v1+0.1v2+0.4v3+0.3v4
5. transformer self attention의 효과
self attention을 활용하니까 단어들이 다양한 방식으로 여러 단어들에 attention할 수 있다.

making이 여러 head에 걸쳐 difficult,more에 attention 가중치가 강하게 나타나고 있음

its가 가리키는 단어가 1번 head에서는 law라고 생각하고 2번 head에서는 application이라고 생각하는 등 여러 문맥적 측면을 고려한다고 볼수있지
'딥러닝 > NLP' 카테고리의 다른 글
| multi-head attentiond 개념 알아보고 간단하게 구현해보기 (1) | 2022.05.02 |
|---|---|
| scaled dot product attention (1) | 2022.05.01 |
| NLP의 역사를 바꾼 self-attention의 기본 원리 (0) | 2022.04.27 |
| NLP에서 한 획을 그은 transformer은 왜 등장했는가 + bidirectional RNN의 특징 (0) | 2022.04.20 |
| length normalization을 이용한 beam search의 종료조건 (0) | 2022.04.19 |

