우리는 $softmax(QK^{T})V$로 attention을 구했지만 논문에서는 scaled dot product attention을 제안했다.
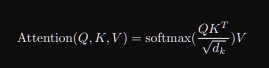
key,query matrix의 차원 $d_{k}$의 제곱근으로 $QK^{T}$를 나눠줬다.
왜 그랬는지 생각해보자.
query와 key의 내적은 언제나 하나의 scalar지만 query,key의 차원 $d_{k}$가 충분히 크다면 내적이 당연히 커진다는 점에 주목했다.
그러면 softmax function이 gradient를 극도로 낮게 만드는 영역이 존재한다는 것이다.
We suspect that for large values of $d_{k}$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients
왜 그래디언트가 작아지는지 그 이유를 이렇게 생각해보라고 제시했다.
To illustrate why the dot products get large, assume that the components of q and k are independent random variables with mean 0 and variance 1. Then their dot product, q · k has mean 0 and variance $d_{k}$
동일하게 한번 생각해보자. x1,x2,x3의 query, key가 2차원으로 다음과 같이 있다고 생각해보자.

query, key의 성분 a,b,x,y가 서로 독립이고 평균이 0, 분산이 1인 random variable이라고 하자.
항상 이렇게 가정할 수 있다. 독립은 사실 아쉬운 가정일수 있지만 query, key는 무슨 값이 들어올지 모르는 하나의 random variable이다.
평균이 0, 분산이 1인 가정은 항상 할 수 있는 가정인데 만약 평균이 0 분산이 1이 안된다면?

평균이 0 분산이 1이되게 정규화시킨 값을 성분으로 대체시켜서 사용하면 되니까 평균이 0, 분산이 1인 것은 항상 할수있는 가정이다.
그러면 이제 a,b,x,y는 서로 독립이고 평균이 0이니까 E(ax+by)=E(ax)+E(by)=E(a)E(x)+E(b)E(y)=0이다.
여기서 a,x가 독립이니까 E(ax)=E(a)E(x)가 성립한다.
Var(ax+by)=Var(ax)+Var(by) 이게 애매하네???

정리하자면 평균이 0, 분산이1이면서 독립인 x,y에 대해 Var(xy)=var(x)var(y)=1이네? 특히 평균이 0이라 성립하구만
참고로 E(X)=0이라고 E(X^2)=0이 아니다 기본인데 왜 그래 새벽이라 그런가?
X=1에서 P=1/2 X= -1에서 P=1/2이면 E(X)=0이지만 E(X^2)=1이다.
아무튼 Var(ax+by)=2가 된다.
여기서 이제 query,key의 차원이 100이면 어떨까?
내적항이 100개면서 평균은 0이지만 분산은 100이다.
무슨말이냐면 query, key의 차원이 $d_{k}$이면 내적의 분산은 $d_{k}$가 된다는 소리임.
그러면 이제 이게 무슨 의미를 가지냐? query,key의 내적인 score는 평균이 0이고 분산이 $d_{k}$인 random variable이 된다는 소리임.
그럴 때 score vector는 어떤식으로 구성이 될까? 이 평균이 0이고 분산이 $d_{k}$인 random variable에서 뽑은 값이 score vector의 성분으로 된다는 소리
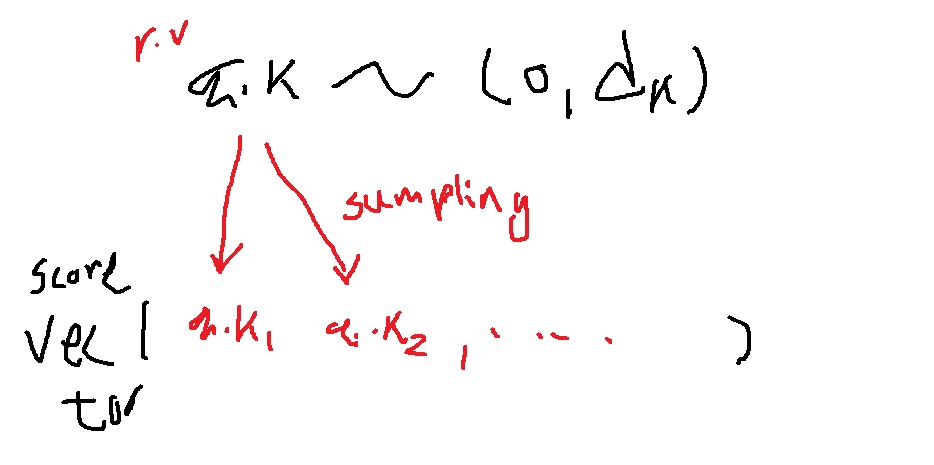
분산이 크다는 말은 random variable로 뽑히는 값들이 편차가 크다는 말이다. 예를 들어 (8,-11,19) 이런식으로 성분간 편차가 크다는 말이다.
분산이 작다는 말은 random variable로 뽑히는 값들이 편차가 작다는 말이다. 예를 들어 (1.1,-0.8,-1.7)로 서로 값들이 비슷하다는 말이다.
그러면 이러한 score vector에 softmax를 취하면 어떨까?
분산이 큰 score vector는 값들간 편차가 크기때문에 softmax를 취한 값들도 극단적인 값들이 된다.
(0.27,0.01,0.72) 이런식으로 어떤 값이 매우 극단적으로 변한다. 그런경우 softmax loss에 의한 gradient는 vanishing 현상이 일어나겠지?

softmax값이 매우 작으면 미분 값이 0에 수렴한다
그러나 분산이 작은 vector는 softmax를 취하면 비슷비슷할것이다.
이렇게 분산이 큰 경우 극단적으로 확률분포가 치우치는 현상을 방지하고자 scaling 요소로 $d_{k}$의 제곱근을 나눈 scaled dot product attention을 수행했다.

'딥러닝 > NLP' 카테고리의 다른 글
| transformer의 메모리 사용량 알아보기 (0) | 2022.05.03 |
|---|---|
| multi-head attentiond 개념 알아보고 간단하게 구현해보기 (1) | 2022.05.02 |
| 예시와 그림으로 이해하는 self attention의 원리 (0) | 2022.04.28 |
| NLP의 역사를 바꾼 self-attention의 기본 원리 (0) | 2022.04.27 |
| NLP에서 한 획을 그은 transformer은 왜 등장했는가 + bidirectional RNN의 특징 (0) | 2022.04.20 |

