1. residual connection
self attention 구조하에 당시 좋은 성능 향상 기법인 residual add connection, layer normalization을 채택했다.

input $X_{t}$의 encoding 결과로 $h_{t}$라는 hidden vector를 얻고 싶은데 multi head attention이 학습하는 결과는$h_{t}-X_{t}$라고 하는 것이며
이 결과에 input $X_{t}$를 그대로 더하여 $h_{t}$라는 목표하는 hidden vector를 얻는다.

input의 (1,4)의 multi head attention 결과로 얻은 (2,3)에 단순히 더하여 (3,7)이라는 벡터를 얻는 과정이 residual connection이다.
입력 input과 multi head attention의 결과인 output의 차원이 동일해야 가능하다.
그렇기 때문에 multi head attention에서 사용된 $W^{O}$에 의한 concat(head)의 선형변환이 input과 output의 차원을 동일하게 맞추는 역할을 한 것이다.
residual connection은 깊은 neural network를 만들때 gradient vanishing을 개선하고 학습성능 향상을 도와준다고 알려져있다.
2. normalization
neural network의 다양한 normalization 기법으로 batch,layer,instance,group등이 있다.
기본 아이디어는 다수의 sample의 평균을 0으로 분산을 1로 만들고 적절한 변환으로 원하는 평균과 분산으로 만들고자 하는 것이다.

3. batch normalization
batch size=3인 3차원의 데이터를 Neural network에 넣는 상황을 생각해보자.
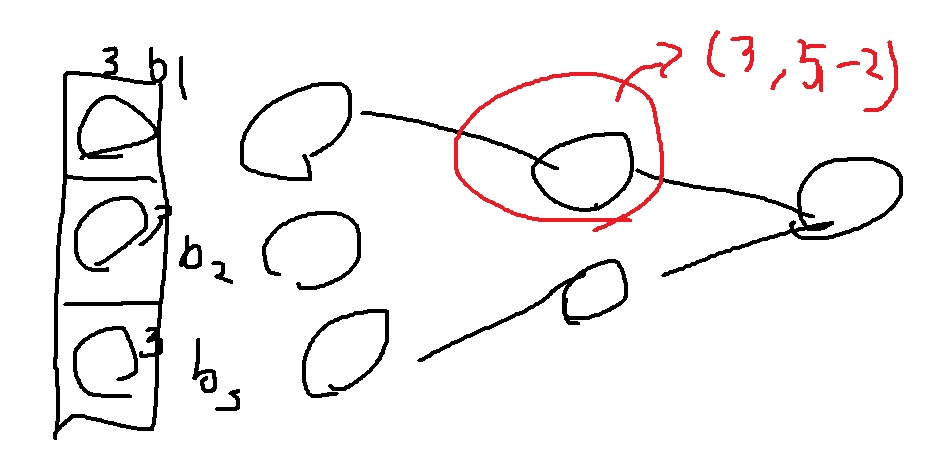
특정 node에서 계산한 결과 각 batch에 대하여 (3,5,-2)라는 결과를 얻었을 때 이들의 평균은 2이므로 (3-2,5-2,-2-2)=(1,3,-4)로 평균을 0으로 만든 뒤
표준편차를 계산하면 $\sqrt{1+9+16} = \sqrt{26}$이므로 $(\frac{1}{\sqrt{26}},\frac{3}{\sqrt{26}},\frac{-4}{\sqrt{26}})$로 만들면 평균이 0 분산이 1로 normalization 된다.
이들의 적절한 transform $y=x\beta+\gamma$를 생각하자.
$\beta$와 $\gamma$는 학습이 가능한 parameter로 최적값이 2,3이라면 $(\frac{1}{\sqrt{26}},\frac{3}{\sqrt{26}},\frac{-4}{\sqrt{26}})$의 변환은
$(\frac{2}{\sqrt{26}} + 3, \frac{6}{\sqrt{26}} + 3 ,\frac{-8}{\sqrt{26}} + 3)$ 이들의 평균은 3이고 분산은 4이다.
$\beta$와 $\gamma$는 특정 node에서 가장 최적화된 평균과 분산을 가지도록 학습한다.
$\beta$와 $\gamma$는 실험자가 원하는 평균과 분산을 주입하는 역할을 한다.
4. layer normalization
layer normalization은 layer 단위에서 normalization을 수행하는 것이다.

특정 layer에 thinking과 machine의 계산 결과가 (4,2,3,5), (2,1,-3,2)이다.
각 벡터에서 계산된 자료의 평균, 표준편차 위와 같이 주어져있다. 이들을 빼고 표준편차로 나눠 평균이 0 분산이 1인 normalization 과정을 거친다.
다음 원하는 평균과 분산을 주입하기 위한 $y=x\beta+\gamma$를 각 node별로(row별로) 변환을 시킨다.
$\beta$와 $\gamma$는 특정 node에서 가장 최적화된 평균과 분산을 가지도록 학습한다.
두 normalization 모두 방법은 약간 다르지만 학습의 안정화와 모델 성능 향상을 가져온다고 알려져있다.
'딥러닝 > NLP' 카테고리의 다른 글
| transformer에 사용된 warm up learning rate scheduler (0) | 2022.05.16 |
|---|---|
| transformer에 사용된 positional encoding에 대하여 (0) | 2022.05.13 |
| transformer의 메모리 사용량 알아보기 (0) | 2022.05.03 |
| multi-head attentiond 개념 알아보고 간단하게 구현해보기 (1) | 2022.05.02 |
| scaled dot product attention (1) | 2022.05.01 |

