최대 50만*50만의 2차원 평면 위에 k개 <= 100의 점이 있다
최대 10만*10만의 L*L 정사각형으로 가장 많은 점을 포함시키려고 할때, 이 정사각형에 포함되지 않는 점의 개수를 구한다
정사각형의 모서리에 포함되어도 포함된 것으로 인정한다
----------------------------------------------------------------------------------------------------------------------------------------------
문제의 조건을 만족하는, 평면 위에 가장 많은 점을 포함하는 정사각형의 배치는 반드시 존재할 수 밖에 없다.
그러한 최적 배치에 들어가있는 모든 별을 포함할 수만 있다면,
정사각형의 배치는 바꿀 수 있다.
그리고 이웃한 두 모서리에 반드시 2개의 별이 포함되도록 이동시킬 수 있다

이게 불가능할 수 있나?
굳이 따지자면 이런 경우? 전부 일렬로 배치된 경우?

근데 상관없긴해
가장 많은 별을 포함하는 최적의 배치가 존재한다면, 정사각형을 적절하게 이동하여 여전히 최적의 배치가 되게할 수 있다
이때 아래쪽 변과 왼쪽 변에 별을 포함하게 정사각형을 이동한다면

점 A의 x좌표와 점 B의 y좌표를 기준으로 잡고
정사각형의 길이가 L이므로, (x,x+L), (y,y+L)에 존재하는 별들의 개수를 세면 된다.
그러면 일렬로 배치된 얘는 왜 상관없다한거임?
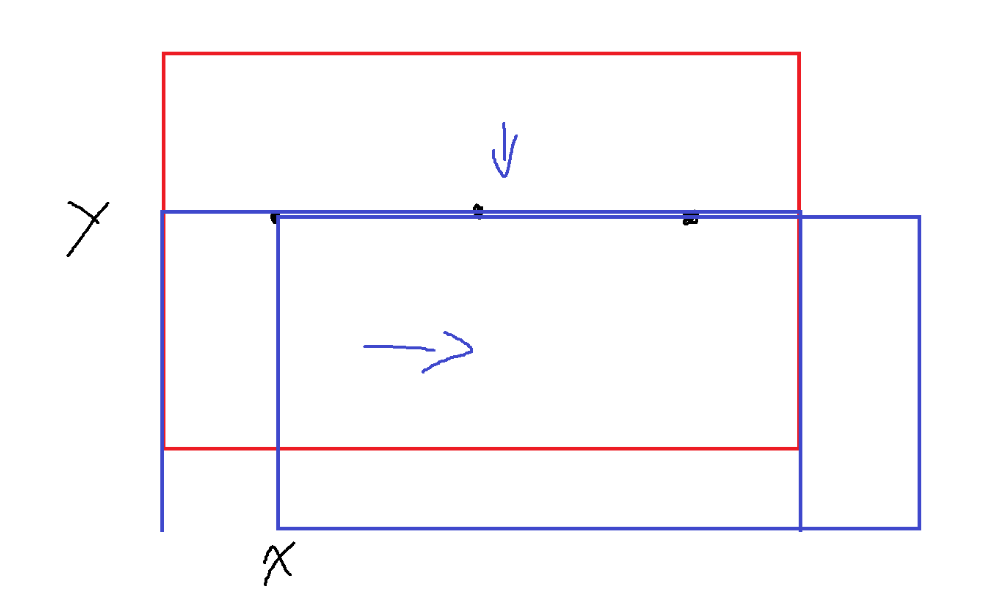
그거야 점 A = 점 B로 같은 경우도 포함해서 계산하면 되니까
따라서 k개의 점의 x좌표에 대하여, k개의 점의 y좌표에 대하여, x,y를 기준으로 잡고
다시 k개의 점의 (a,b)좌표를 모두 검사해서 (x,x+l),(y,y+l)에 포함되는 것의 개수를 세서
가장 큰 경우를 찾는다
from sys import stdin
n,m,l,k = map(int,stdin.readline().split())
A = []
for _ in range(k):
a,b = map(int,stdin.readline().split())
A.append((a,b))
answer = 0
for i in range(k):
for j in range(k):
x,y = A[i][0],A[j][1]
count = 0
for a,b in A:
if a >= x and a <= x+l and b >= y and b <= y+l:
count += 1
answer = max(answer,count)
print(k-answer)
풀진 않았는데 두 문제랑 똑같은 문제라네
생각안날때 풀어보는걸로
'알고리즘 > 브루트포스' 카테고리의 다른 글
| 가로 세로 선 3개만 그어서 모든 점을 덮을 수 있는가? (0) | 2024.11.18 |
|---|---|
| 수천개의 점들 중에서 가장 넓이가 큰 정사각형을 찾는 방법 (0) | 2024.11.17 |
| 탐색 범위를 줄여야하는 브루트포스 연습4 - 평면 위에 직사각형 쳐서 점 고르기 (0) | 2024.11.15 |
| 탐색 범위를 줄여야하는 브루트포스 연습3 - 해밍 수열의 i번째 수 찾기 (0) | 2024.11.11 |
| 숨어있는 기준을 찾는 브루트포스1 - 수많은 좌표들을 얼마나 평행이동해야 일치하는가 (0) | 2024.11.09 |

