n개의 점이 있는데 수직선이나 수평선으로 3개만 그어서 모든 점을 덮을 수 있는지 체크하는 문제
점의 좌표 범위가 10^9이다 보니 하나하나 다 그어보면 당연히 시간초과 날것이고
X좌표를 기준으로 그룹을 묶고, Y좌표를 기준으로 그룹을 묶는다
그러면 어떤 X = x좌표를 기준으로 수직선을 그어보면, 해당하는 y좌표들을 알 수 있다
그러면 그러한 y좌표가 여러개 있다면?
Y = y로 수평선을 또 그어야할 것이다

근데 해당하는 Y = y2가 하나만 존재한다면 Y = y2로 수평선을 그을 필요가 없다

그러므로 모든 X = x에 대해 순회해봐서 x에 대응하는 y들을 다시 하나씩 순회해본 다음
해당하는 y좌표값들 개수가 2개 이상인 경우가 존재하면 그 쪽으로 수평선을 그어야하므로,
이미 수직선을 하나 그은 상태이기 때문에, 수평선은 최대 2개만 그을 수 있으니
y좌표값들 개수가 2개 이상인 경우가 2개 이하로 존재하는 경우가 발견되면 True
from sys import stdin
n = int(stdin.readline())
X = {}
X_count = {}
Y = {}
Y_count = {}
for _ in range(n):
x,y = map(int,stdin.readline().split())
if X.get(x,0) == 0:
X[x] = set()
X[x].add(y)
X_count[x] = X_count.get(x,0) + 1
if Y.get(y,0) == 0:
Y[y] = set()
Y[y].add(x)
Y_count[y] = Y_count.get(y,0) + 1
이렇게 x좌표, y좌표 기준으로 각각 대응하는 좌표들을 그룹으로 묶은 다음
x좌표 y좌표 각각 개수들도 구해놓고
find = False
for x in X:
count = 0
for y in X[x]:
if Y_count[y] == 1:
count += 1
if len(Y) - count <= 2:
find = True
break
if find:
print(1)
X에서 x좌표에 대해 x좌표에 대응하는 y좌표들 X[x]들을 순회해서...
해당하는 y가 1개만 있다면 counting을 해주고
전체 y의 개수는 len(Y)이고 수평선으로 안그어도 되는 개수 count를 빼준 len(Y) - count는
수평선으로 그어야하는 개수이며, 이것이 2 이하이면 3개 선분으로 모두 덮을 수 있다는 뜻
근데... 여기서 Y_count[y] == 1인 경우 counting했는데 Y_count[y] >= 2인 경우 counting해서
그 count는 수평선으로 그어야하는 개수니까 그게 2 이하여도 되는거 아닌가?
find = False
for x in X:
count = 0
for y in X[x]:
if Y_count[y] >= 2:
count += 1
if count <= 2:
find = True
break
if find:
print(1)
근데 이렇게 하면 틀리는게... X[x]에는 모든 y가 들어있는게 아니다
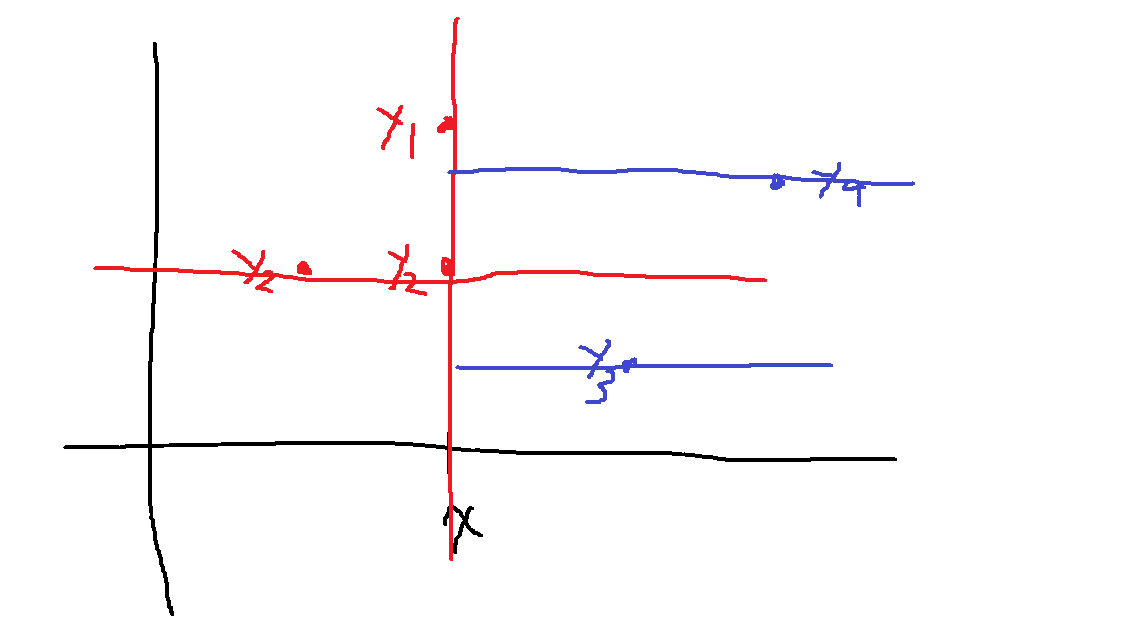
다음과 같은 경우 X[x]에는 y1,y2가 들어있는데... y2가 2개니까 수평선으로 하나만 그어서
count <= 2라서 find = True가 되지만...
실제로는 y3,y4도 존재하고 그쪽으로는 반드시 수평선을 그어야하므로 실제로는 4개 필요함
X좌표에 대해서도 해봤으니까 Y좌표에 대해서도 똑같이 검사해서...
from sys import stdin
n = int(stdin.readline())
X = {}
X_count = {}
Y = {}
Y_count = {}
for _ in range(n):
x,y = map(int,stdin.readline().split())
if X.get(x,0) == 0:
X[x] = set()
X[x].add(y)
X_count[x] = X_count.get(x,0) + 1
if Y.get(y,0) == 0:
Y[y] = set()
Y[y].add(x)
Y_count[y] = Y_count.get(y,0) + 1
if len(X) <= 3 or len(Y) <= 3:
print(1)
else:
find = False
for x in X:
count = 0
for y in X[x]:
if Y_count[y] == 1:
count += 1
if len(Y) - count <= 2:
find = True
break
if find:
print(1)
else:
for y in Y:
count = 0
for x in Y[y]:
if X_count[x] == 1:
count += 1
if len(X) - count <= 2:
find = True
break
if find:
print(1)
else:
print(0)
처음에 if len(X) <= 3 or len(Y) <=3은 X좌표 개수가 3개 이하거나 Y좌표 개수가 3개 이하이면...
무조건 선분 3개로 전부 덮을 수 있기 때문에 바로 1을 출력하면 됨
--------------------------------------------------------------------------------------------------------------------------------------------------------
다른 풀이로는 모든 점이 선분에 덮이기 때문에, 모든 점은 적어도 하나의 선분 위에 존재해야한다는 점을 이용
그래서 0번 점을 먼저 기준으로 수평선 혹은 수직선을 그어보고, 그어지지 않은 점을 하나 잡아서,
그 점을 기준으로 수평선 혹은 수직선을 또 그어보고, 그어지지 않은 점을 하나 잡아서
또 수평선 혹은 수직선을 그어본 다음, 모든 점이 덮여있는지 체크
재귀적으로 다음과 같이
from sys import stdin
n = int(stdin.readline())
A = []
X = {}
Y = {}
for i in range(n):
x,y = map(int,stdin.readline().split())
if X.get(x,0) == 0:
X[x] = set()
X[x].add((y,i))
if Y.get(y,0) == 0:
Y[y] = set()
Y[y].add((x,i))
A.append((x,y))
visited = [0]*n
def dfs(j,s):
if j == -1:
return True
if s == 3:
return False
x,y = A[j]
for yy,i in X[x]:
visited[i] += 1
p = -1
for k in range(n):
if visited[k] == 0:
p = k
break
if dfs(p,s+1):
return True
for yy,i in X[x]:
visited[i] -= 1
for xx,i in Y[y]:
visited[i] += 1
p = -1
for k in range(n):
if visited[k] == 0:
p = k
break
if dfs(p,s+1):
return True
for xx, i in Y[y]:
visited[i] -= 1
return False
f = dfs(0,0)
if f:
print(1)
else:
print(0)
여기서 핵심은 visited[i] = 1로 선을 긋고 visited[i] = 0으로 선을 지우는게 아니라
visited[i] += 1로 선을 긋고 visited[i] -= 1로 선을 지우는 것
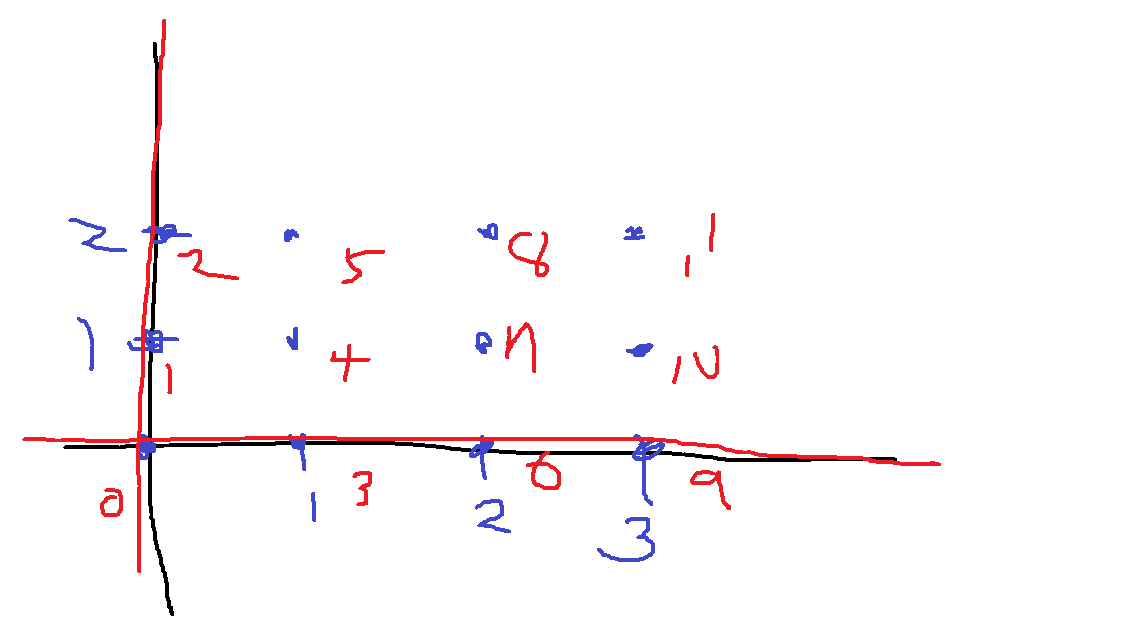
visited[i] = 1, visited[i] = 0으로 선 긋고 선 지우면 위와 같은 경우 X = 0, Y = 0에 선을 그었을때,
X = 0을 지우고 Y = 1로 선을 그을려는 과정에서
visited[0] = 1, visited[1] = 1, visited[2] = 1, visited[3] = 1, visited[6] = 1, visited[9] = 1인데
X = 0을 지우면 visited[0] = 0, visited[1] = 0, visited[2] = 0으로 되어버려서 vistied[3] = 1, visited[6] = 1, visited[9] = 1만 남는다
근데 문제는 visited[0] = 1로 해야 문제가 없는데...
이를 방지하기 위해서 1씩 증가, 1씩 감소시키는 방법으로 구현
또 하나 주목할 만한 테크닉은
if dfs(p,s+1): return True
dfs() 결과가 True가 나오면 True를 return해서 그 아래 코드는 실행하지 않도록
False가 나오면 그 아래 코드를 실행하도록
return dfs(p,s+1)로 해버리면, 그 아래 코드는 False가 나오더라도 실행이 안되거든
그래서 if문을 이용해서 ./ False가 나오면 아래 코드가 실행될 수 있도록
x,y = A[j]
for yy,i in X[x]:
visited[i] += 1
p = -1
for k in range(n):
if visited[k] == 0:
p = k
break
if dfs(p,s+1):
return True
for yy,i in X[x]:
visited[i] -= 1
'알고리즘 > 브루트포스' 카테고리의 다른 글
| 가장 많은 점을 포함하는 사각형 찾기 놀라운 방법 (0) | 2025.03.30 |
|---|---|
| 수천개의 점들 중에서 가장 넓이가 큰 정사각형을 찾는 방법 (0) | 2024.11.17 |
| 탐색 범위를 줄여야하는 브루트포스 연습4 - 평면 위에 직사각형 쳐서 점 고르기 (0) | 2024.11.15 |
| 탐색 범위를 줄여야하는 브루트포스 연습3 - 해밍 수열의 i번째 수 찾기 (0) | 2024.11.11 |
| 숨어있는 기준을 찾는 브루트포스1 - 수많은 좌표들을 얼마나 평행이동해야 일치하는가 (0) | 2024.11.09 |

