평면 위 n개의 점이 있는데, 세로로 A, 가로로 B인 직사각형을 쳐서 이 안에 있는 점의 크기의 최댓값과 최솟값의 차이가
가장 크게 직사각형을 만들고 싶다
보면 N <= 1000인데 점의 좌표는 (R,C) <= 2*10^6이고 A,B <= 2*10^6임
그러다보니 직사각형의 크기를 1부터 2*10^6까지 돌리고 직사각형 위치를 2*10^6*2*10^6... 해보면.. 당연히 시간초과
그런데 구하고자 하는 것이 직사각형 크기 이런건 아니고 아무 직사각형이나 쳐서 그 안에 점 크기의 최댓값 - 최솟값의 차이를 최대로 만드는거
어떤 점들이 들어오느냐 이게 중요
그래서 점 i를 기준으로 잡아서 점 j를 순회해서 크기가 A*B인 직사각형을 만들 수 있는지 고려해보고
가능하다면 두 점 i,j는 직사각형 내부에 있기 때문에 두 점 i,j의 크기를 최댓값, 최솟값으로 갱신해서 하면 된다는거
처음에 푼 풀이는 엄청 복잡하게? 풀었네
나름 머리 써서 점 i를 기준으로 잡고 점 j를 순회하는데 점 j가 점 i를 기준으로 어디에 위치하느냐에 따라...
4군데로 나눠서 푼듯?

from sys import stdin
n,a,b = map(int,stdin.readline().split())
A = []
for i in range(n):
r,c,s = map(int,stdin.readline().split())
A.append((r,c,s))
answer = 0
for i in range(n):
r,c,s = A[i]
max_s = s
min_s = s
for j in range(n):
rr,cc,ss = A[j]
if rr >= r and rr <= r+a-1 and cc >= c and cc <= c+b-1:
if max_s < ss:
max_s = ss
if min_s > ss:
min_s = ss
if answer < max_s - min_s:
answer = max_s - min_s
max_s = s
min_s = s
for j in range(n):
rr,cc,ss = A[j]
if rr >= r and rr <= r+a-1 and cc <= c and cc >= c-b+1:
if max_s < ss:
max_s = ss
if min_s > ss:
min_s = ss
if answer < max_s - min_s:
answer = max_s - min_s
max_s = s
min_s = s
for j in range(n):
rr,cc,ss = A[j]
if rr <= r and rr >= r-a+1 and cc >= c and cc <= c+b-1:
if max_s < ss:
max_s = ss
if min_s > ss:
min_s = ss
if answer < max_s - min_s:
answer = max_s - min_s
max_s = s
min_s = s
for j in range(n):
rr,cc,ss = A[j]
if rr <= r and rr >= r-a+1 and cc <= c and cc >= c-b+1:
if max_s < ss:
max_s = ss
if min_s > ss:
min_s = ss
if answer < max_s - min_s:
answer = max_s - min_s
print(answer)
근데 어쨌든 핵심은 직사각형을 기준으로 위치를 옮기면서 하는게 아니라
두 점을 기준으로 잡아서 각 두 점이 최댓값, 최솟값이라고 가정하고
이 두 점을 포함하는 크기 A*B인 직사각형을 만들 수 있는지 없는지 체크해보면 된다
두 점 (r,c)와 (rr,cc)에서 x좌표 크기 차이 |rr-r|이 b-1이내이고 y좌표 크기 차이 |cc-c|가 a-1이내이면
크기 A*B인 어떤 직사각형이 이 두 점을 반드시 포함할 수 있다
왜 크기가 A*B라면서 a-1,b-1이냐고?
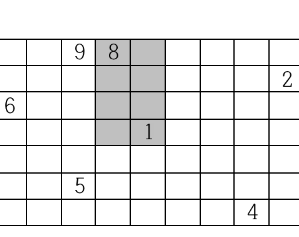
(4,0)인 8이랑 (5,3)인 1을 보면 X 좌표 차이가 1인데 직사각형 가로 길이는 2임
마찬가지로 Y좌표 차이가 3인데 세로 길이는 4임
아무튼 그 직사각형 내부에 여러 점이 있을 수 있지만, 최댓값, 최솟값은 이 두 점 (r,c), (rr,cc)라고 가정하고 브루트포스를 하는거
물론 이 직사각형 내부에 최댓값, 최솟값인 다른 점 (r',c'), (rr',cc')이 있을 수 있지
근데 이 경우는 두 점을 기준으로 브루트포스하면서 알아서 체크 된다는거지
from sys import stdin
n,a,b = map(int,stdin.readline().split())
A = []
for i in range(n):
r,c,s = map(int,stdin.readline().split())
A.append((r,c,s))
answer = 0
for i in range(n):
r,c,s = A[i]
for j in range(n):
rr,cc,ss = A[j]
if abs(r-rr) <= a-1 and abs(c - cc) <= b-1:
if answer < s - ss:
answer = s - ss
print(answer)
'알고리즘 > 브루트포스' 카테고리의 다른 글
| 가로 세로 선 3개만 그어서 모든 점을 덮을 수 있는가? (0) | 2024.11.18 |
|---|---|
| 수천개의 점들 중에서 가장 넓이가 큰 정사각형을 찾는 방법 (0) | 2024.11.17 |
| 탐색 범위를 줄여야하는 브루트포스 연습3 - 해밍 수열의 i번째 수 찾기 (0) | 2024.11.11 |
| 숨어있는 기준을 찾는 브루트포스1 - 수많은 좌표들을 얼마나 평행이동해야 일치하는가 (0) | 2024.11.09 |
| 브루트포스 문제 복기하면서 실수한 부분 체크하기1(어디서든 시작할 수 있다) (0) | 2024.10.26 |

