점이 n개 <= 3000가 있을 때 가장 넓이가 큰 정사각형을 찾는 문제
그냥 한다면 O(N^4)이겠지만 당연히 안될거고
O(N^3)인 방법도 있긴한데 N <= 3000이다보니 어렵다
정사각형 성질을 이용하면.. 임의의 두 점 A(x1,y1), B(x2,y2)을 먼저 잡고 벡터 AB를 구한다
벡터 AB = OB - OA = (x2-x1, y2-y1)으로 구할 수 있다

다음 벡터 AB를 시계방향으로 90도 회전하면 벡터 AD를 구할 수 있다
90도 회전하는 방법은?
(x,y) >> (-y,x)로 되므로 벡터 AD = (-y2+y1, x2-x1)이 된다
https://deepdata.tistory.com/1388
벡터 (x,y)를 90도 회전하는 방법
1. 회전 행렬 벡터 (x,y)는 극좌표계를 이용하면 $(rcos \theta , rsin \theta)$ 이 상황에서 A만큼 회전시킨다면... Q의 좌표는 $(rcos (\theta + A), rsin (\theta + A))$ 삼각함수의 덧셈정리를 이용하면 $cos
deepdata.tistory.com

만약 D의 좌표를 (x',y')이라고 하면, 벡터 AD = (y1-y2, x2-x1)이므로,
(x'-x1, y'-y1) = (y1-y2,x2-x1)이므로, x' = x1 + (y1-y2), y' = y1 + (x2-x1)으로 구할 수 있다
그리고 벡터 AD는 평행이동하면... 벡터 BC가 된다.
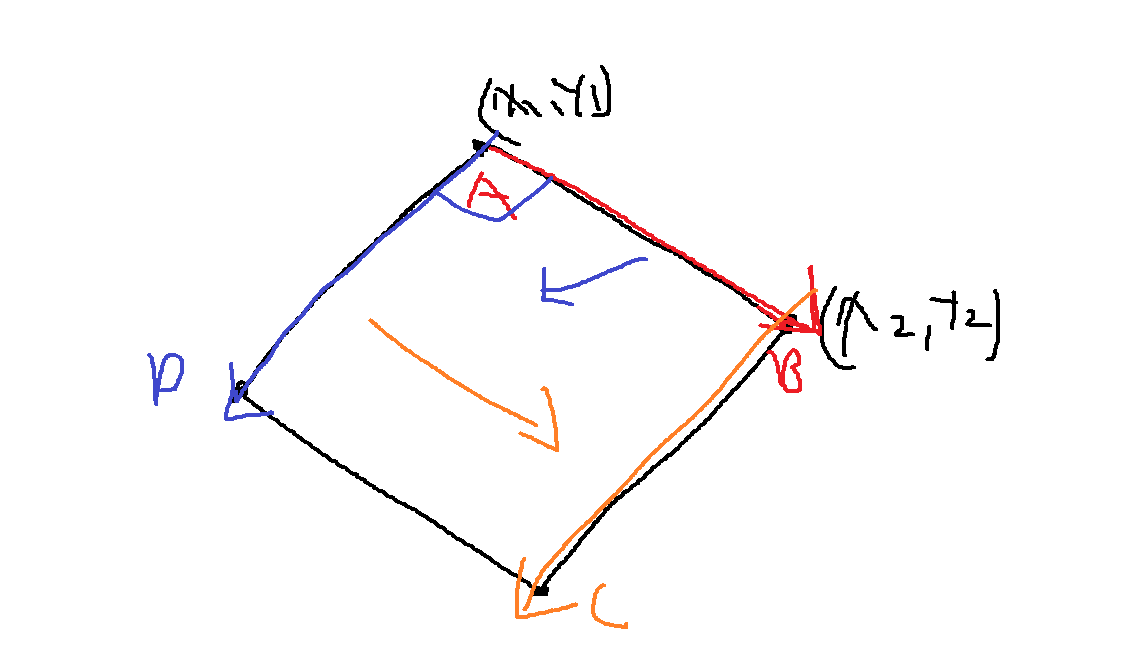
따라서 C의 좌표가 (x',y')이라면 (x'-x2, y'-y2) = (y1-y2, x2-x1)이므로,
x' = x2 + (y1-y2), y' = y2+(x2-x1)이다.
그러므로 (x1,y1), (x2,y2)를 알고 있다면 정사각형을 이루는 나머지 두 점을 구할 수 있다.
그래서 (x1,y1), (x2,y2)를 잡고 나머지 두 점을 구한 다음, 이 나머지 두 점이 평면상에 실제로 존재하는지 hash로 체크하면 된다
from sys import stdin
T = int(stdin.readline())
for _ in range(T):
n = int(stdin.readline())
A = []
H = {}
for _ in range(n):
x,y = map(int,stdin.readline().split())
A.append((x,y))
H[(x,y)] = 1
answer = 0
for i in range(n):
x1,y1 = A[i]
for j in range(n):
x2,y2 = A[j]
if i == j:
continue
v = (x2-x1,y2-y1)
vv = (-v[1],v[0])
x3,y3 = x2-v[1],y2+v[0]
x4,y4 = x1-v[1],y1+v[0]
if H.get((x3,y3),0) == 1 and H.get((x4,y4),0) == 1:
s = v[0]**2 + v[1]**2
if answer < s:
answer = s
print(answer)
여기서 정사각형 넓이는.. 벡터 (x2-x1, y2-y1)의 크기 제곱과 같기 때문에.. 루트를 취하지 않아도
정수형 연산으로 구할 수 있다는거
'알고리즘 > 브루트포스' 카테고리의 다른 글
| 가장 많은 점을 포함하는 사각형 찾기 놀라운 방법 (0) | 2025.03.30 |
|---|---|
| 가로 세로 선 3개만 그어서 모든 점을 덮을 수 있는가? (0) | 2024.11.18 |
| 탐색 범위를 줄여야하는 브루트포스 연습4 - 평면 위에 직사각형 쳐서 점 고르기 (0) | 2024.11.15 |
| 탐색 범위를 줄여야하는 브루트포스 연습3 - 해밍 수열의 i번째 수 찾기 (0) | 2024.11.11 |
| 숨어있는 기준을 찾는 브루트포스1 - 수많은 좌표들을 얼마나 평행이동해야 일치하는가 (0) | 2024.11.09 |

