1. 회전 행렬
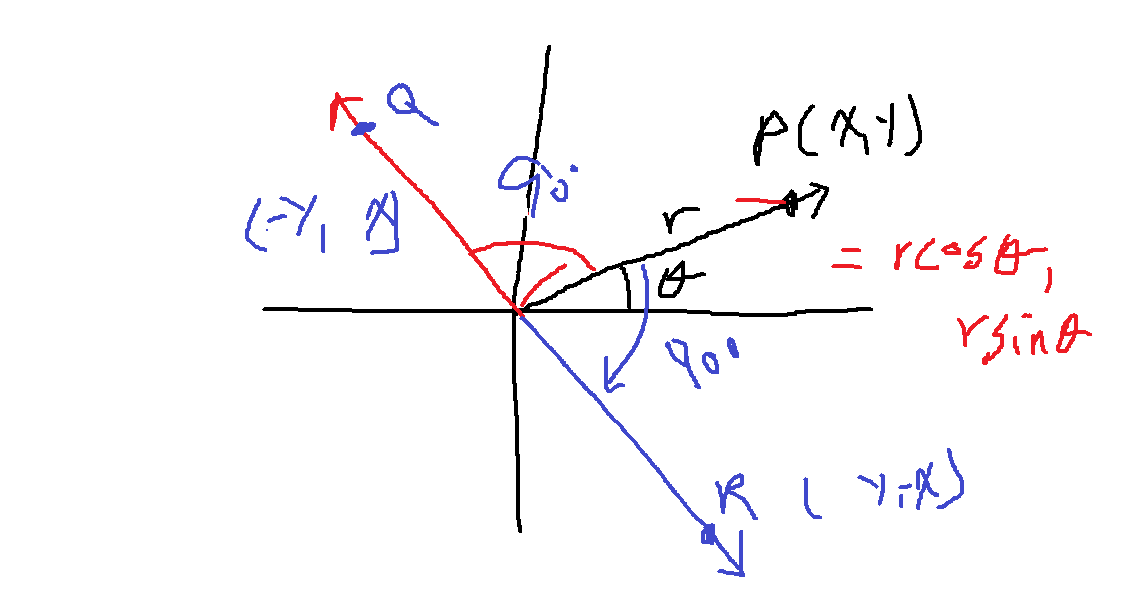
벡터 (x,y)는 극좌표계를 이용하면 $(rcos \theta , rsin \theta)$

이 상황에서 A만큼 회전시킨다면... Q의 좌표는 $(rcos (\theta + A), rsin (\theta + A))$

삼각함수의 덧셈정리를 이용하면 $cos (\theta + A) = cos \theta * cosA - sinA * sin \theta $이고
$sin (\theta + A) = sin \theta * cos A + cos \theta * sin A$
$x = rcos \theta, y = rsin \theta$이므로 이를 대입하면...
$x' = rcos (\theta + A) = x cos A - y sin A, y' = rsin (\theta + A) = ycosA + xsinA$
따라서 Q(x',y')과 P(x,y)는 다음과 같은 관계가 성립한다
$$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} cosA & -sinA \\ sinA & cos A \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$
2. 90도 회전
반시계방향으로 A = 90'라면, cos90' = 0, sin90' = 1이므로 x' = -y, y' = x가 되니까 (x',y') = (-y,x)
시계방향으로 A = -90'라면 cos-90' = 0, sin-90' = -1이므로 x' = y, y' = -x가 되니까 (x',y' = (y,-x)
'기하학' 카테고리의 다른 글
| 좌표평면 위의 모든 점들에서 거리 합이 가장 가까운 점을 찾는 방법 (0) | 2025.08.18 |
|---|---|
| 평면 위 두 직사각형이 서로 겹치는 직사각형의 좌표 구하는 놀라운 방법 (0) | 2024.08.29 |
| 사각형과 원이 겹치는 영역의 좌표의 개수는 O(N)에 구할 수 있을까 (0) | 2024.08.01 |
| 원 안에 원을 가득 채우는 문제?(circle packing in a circle) (0) | 2024.07.27 |
| 꼭짓점이 둥근 볼록껍질(round convex hull)의 둘레의 길이를 구하는 법 (0) | 2023.09.27 |

