E - Alphabet Tiles (atcoder.jp)
E - Alphabet Tiles
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
대문자 알파벳 A,B,C,..,Z의 개수가 주어질때, 이들로 만들 수 있는 길이 1부터 k까지 모든 문자열의 개수를 구하는 문제
길이가 s일때, 각각 A,B,C,...,Z 문자가 a1,a2,a3,...,a26개 있다고 한다면..
이들을 일렬로 배열하는 복수순열의 개수와 같으므로,
$$\frac{(a1+a2+a3+...+a26)!}{a1!a2!...a26!} = \frac{s!}{a1!a2!...a26!}$$
그러면 주어진 배열 C로 만들 수 있는 가능한 모든 (a1,a2,a3,..,a26)의 조합에 대해 위 값들의 합을 구하면 된다.
1. 다항식의 곱으로 구하는 방법
쉽게 생각하기 위해 예를 들어 C = (1,1,0,0,0,0,...,0)이라고 생각해보면?
최대 길이가 2인 문자열들의 개수는
0 0
0 1
1 0
1 1
의 조합으로 만들어지는 복수 순열의 합이다.
이는 다음과 같이 다항식으로 생각해서, 다항식의 계수에 길이의 팩토리얼값을 곱한 값들의 합으로 구할 수 있다

여기서 길이가 1 이상이니까 상수항은 제외해야한다..
만약 최대 길이가 1인 문자열의 개수를 구해야한다면?
1 0
0 1
2가지 경우이므로, 1차항의 계수들의 합만 구하면 된다.
따라서, C = [c1,c2,...,c26]으로 사용할 수 있는 문자의 개수가 주어지고, 최대 길이 K인 문자열의 개수를 구하고자 한다면
다음과 같은 다항식을 26개 만들고
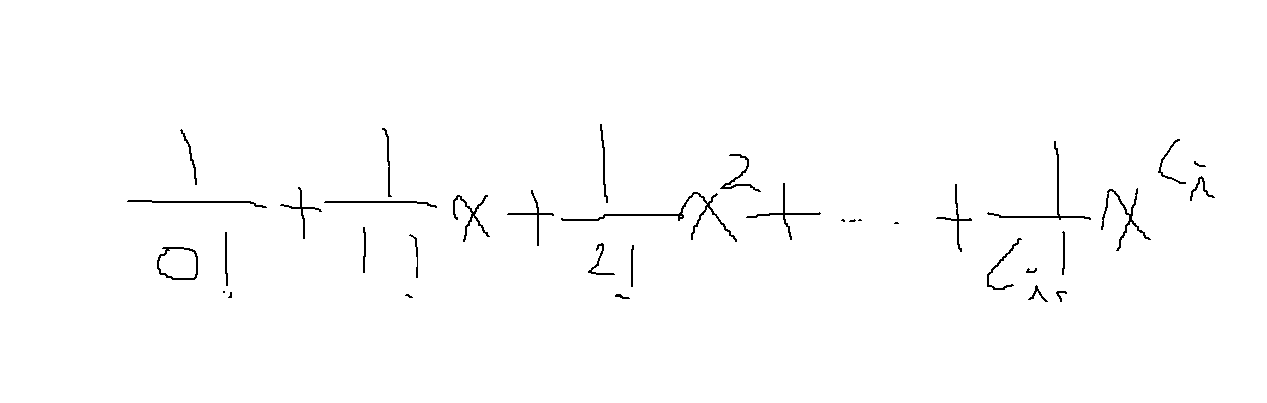
이 26개 다항식의 곱을 구해서 1차항부터 K차항의 각 계수에 길이 L의 팩토리얼 L!을 곱한 값들의 합을 구하면 될 것이다.
두 다항식 N1차 N2차의 곱은 O(N1N2)에 가능하다.
https://deepdata.tistory.com/981
다항식의 곱셈과 나눗셈 기본 컴퓨터 구현 방법 배우기
1. 다항식의 곱셈 두 다항식의 곱셈은 구현하는 방법이 많이 있지만... 당장은 어려우니 일단 $O(k^{2})$으로 naive하게 구현 해보자. 다항식은 각 항의 계수를 배열에 저장하면 되는데 $f(x) = 2x^{2} + x
deepdata.tistory.com
def multiply(a,b,mod):
result = [0]*(len(a) + len(b) + 1)
for i in range(len(a)):
for j in range(len(b)):
result[i+j] += (a[i]*b[j])%mod
return result
1개의 다항식의 계수가 최대 1000까지 가능하므로,
2개의 다항식을 곱하면 2000
3개를 곱하면 3000...
26개를 곱하면 26000...
계속 늘어나다보니까 시간초과날 것 같은데
필요한건 k차항 계수 이하만 필요하고 두 다항식의 곱을 잘 생각해보면... k+1차항부터는 k차항에 관여하지 않는다.
2차식 * 2차식 = 4차식인데, 1차항을 만드는건 1차항 * 0차항, 0차항 * 1차항이지, 2차항은 1차항을 만들지 못한다.
따라서 len(a)차항 len(b)차항을 곱할때, len(a) + len(b)차항으로 만들지 말고, 항상 k차항으로 만들도록 한다.
def multiply(a,b,k,mod):
result = [0]*(k+1)
for i in range(len(a)):
for j in range(len(b)):
if i+j > k:
break
result[i+j] += (a[i]*b[j])%mod
return result
for문에서 i + j > k이면 break시켜서 탈출하도록 만들면 $O(K^{2})$에 두 다항식을 곱할 수 있다.
모든 가능한 계수 합을 mod = 998244353으로 나눈 값을 구해야하니까 미리 mod로 나눈 값을 구하도록 한다.
다항식을 생성할때, 각 다항식의 계수가 팩토리얼의 역수이므로...
inverse factorial을 구해줘야한다
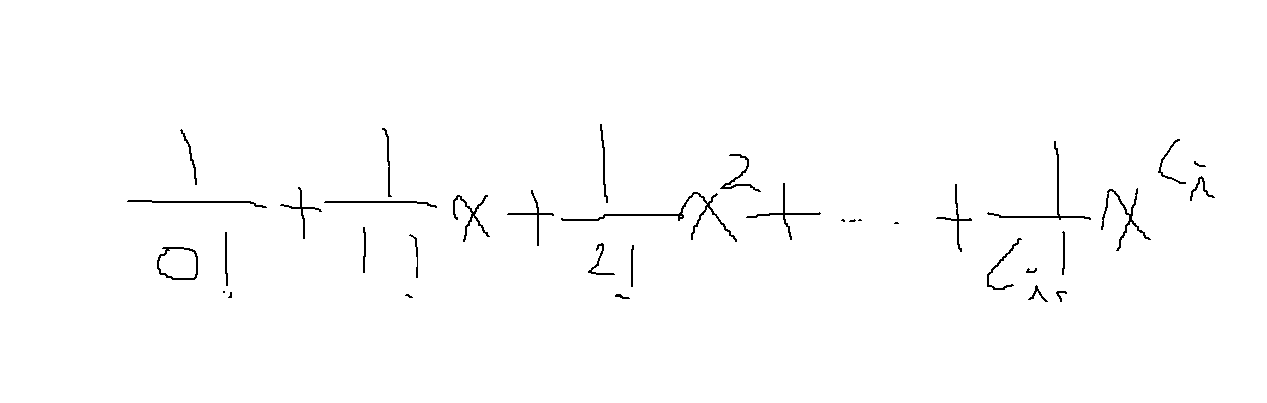
factorial과 inverse factorial은 점화식으로 간단하게 구할 수 있다
https://deepdata.tistory.com/1151
팩토리얼(factorial)의 소수 모듈로 곱셈의 역원(modulo inverse)을 구하는 기본적인 테크닉
이미 알고있는 것들인데 블로그에 정리가 안되어 있어서 1. n!을 소수 p로 나눈 나머지 소수 p에 대하여 $n! mod p$를 구하는 문제가 있다. 단 하나의 $n! mod p$를 구해야한다면... $n! = n*(n-1)*(n-2)*...*1$
deepdata.tistory.com
def factorial(n):
f = [0]*(n+1)
f[0] = 1
for i in range(1,n+1):
f[i] = f[i-1] * i
f[i] %= mod
return f
f = factorial(1000)
def inverse(n,f):
i = [0]*(n+1)
i[n] = pow(f[n],mod-2,mod)
for j in range(n-1,-1,-1):
i[j] = i[j+1] * (j+1)
i[j] %= mod
return i
inv = inverse(1000,f)
모든 준비작업이 끝났으니.. 26번 반복문에서...
각 반복문마다 다항식 1개씩 만들고...
두 다항식 A와 g의 곱을 A로 한 다음...
반복문이 끝나면 1차부터 K차까지, 계수들에 길이 i의 팩토리얼값을 곱한 값의 합으로 구해주면...
$O(26K^{2})$으로 문제를 해결할 수 있다
#26개 다항식을 곱한 결과
A = [0]*(k+1)
A[0] = 1
for i in range(26):
#inverse factorial을 계수로 가지는 다항식 1개를 생성
g = [0]*(C[i]+1)
for j in range(C[i]+1):
g[j] = inv[j]
#A와 g의 곱을 A로 두고...
A = multiply(A,g,k,mod)
answer = 0
#A에는 26개 다항식의 곱의 K차항 계수까지 구해져있다
#1차부터 K차항 계수까지, 각 계수에 길이 i의 factorial값을 곱한 값을 다 더하면...
for i in range(1,k+1):
answer += A[i]*f[i]
answer %= mod
print(answer)
'조합론' 카테고리의 다른 글
| m면체 주사위 n개를 굴려서 나올 수 있는 경우의 수를 구하는 방법 (0) | 2024.08.17 |
|---|---|
| 경기장 일렬 좌석에 앉을 때 사람을 지나치지 않고 전부 앉는 방법의 수 (0) | 2024.07.26 |
| 원형테이블에 앉은 n명의 사람 중 서로 인접하지 않은 k명의 사람을 뽑는 방법 (0) | 2024.06.07 |
| n명 중 k명을 중복해서 선택하는 중복조합의 수 이해하기 (0) | 2024.06.07 |
| 적어도 1명 이상이 자기 자신 것을 그대로 가져갈 확률은?(교란순열의 수렴) (0) | 2024.05.08 |

