1. 다항식의 곱셈
두 다항식의 곱셈은 구현하는 방법이 많이 있지만... 당장은 어려우니 일단 $O(k^{2})$으로 naive하게 구현 해보자.
다항식은 각 항의 계수를 배열에 저장하면 되는데
$f(x) = 2x^{2} + x + 1$이라고 한다면, a = [1,1,2]로 저장하면 된다.
곱셈하고자 하는 다항식이 $g(x) = x + 5$라고 한다면 b = [5,1]이고
두 다항식의 곱셈은 $f(x)g(x) = 2x^{3} + 11x^{2} + 6x + 5$로 [5,6,11,2]가 나와야한다.
f(x)가 len(a)-1차수 다항식이고 g(x)가 len(b)-1차수 다항식이면, f(x)g(x)는 len(a)+len(b)-2차수 다항식이다.
위에서 len(a) = 3, len(b) = 2이고 각각 2차 1차 다항식인데, 곱하면 3차 다항식이다.
이 때 배열의 크기는 len(a)+len(b)-1이다.
또한 f(x)의 i차항이랑 g(x)의 j차항이 곱해진다면, f(x)g(x)에는 i+j차항으로 된다.
result[i+j] += a[i]*b[j]로 구해주면 될듯
#naive polynomial multiplication
def multiply(a,b,mod):
result = [0]*(len(a)+len(b)-1)
for i in range(len(a)):
for j in range(len(b)):
result[i+j] += (a[i]*b[j]) % mod
return result
a = [1,1,2]
b = [5,1]
print(multiply(a,b,10**9+7))
[5,6,11,2]
2. 다항식의 나눗셈
다항식의 나눗셈을 컴퓨터로 구현하기 전에 어떻게 하는지 생각부터 해보자.
$f(x) = 3x^{3} -2x^{2} +x -1$이고, $g(x) = x^{2} - x - 1$이라고 하자.
f(x)/g(x)는 어떻게 구할 수 있을까?
최고차항부터 순서대로 순회하면서, 몫의 최고차항을 결정하고, 나누는 다항식 g(x)와 곱하여 f(x)에 빼는 과정을 반복한다.
뺀 결과의 최고차수가 나누는 다항식 g(x)의 차수보다 작다면 멈춘다.
먼저 몫을 3x로 결정하면, f(x)의 $3x^{3}$을 없앨 수 있다.

그러면 3x를 $x^{2} - x - 1$ 각각에 곱해서...
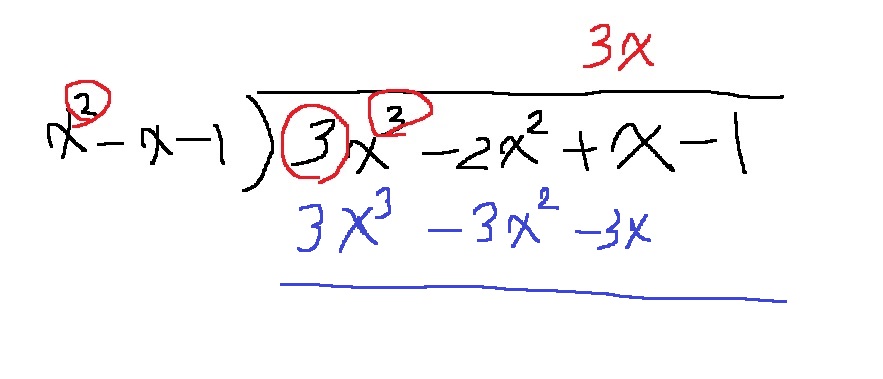
그러면 $3x^{3} - 3x^{2} - 3x$가 되는데 이걸 $f(x) = 3x^{3} - 2x^{2} + x-1$에 빼주면...

$x^{2} + 4x - 1$이 되는데, 이제 몫을 1로 하면, $x^{2}$을 없앨 수 있다.
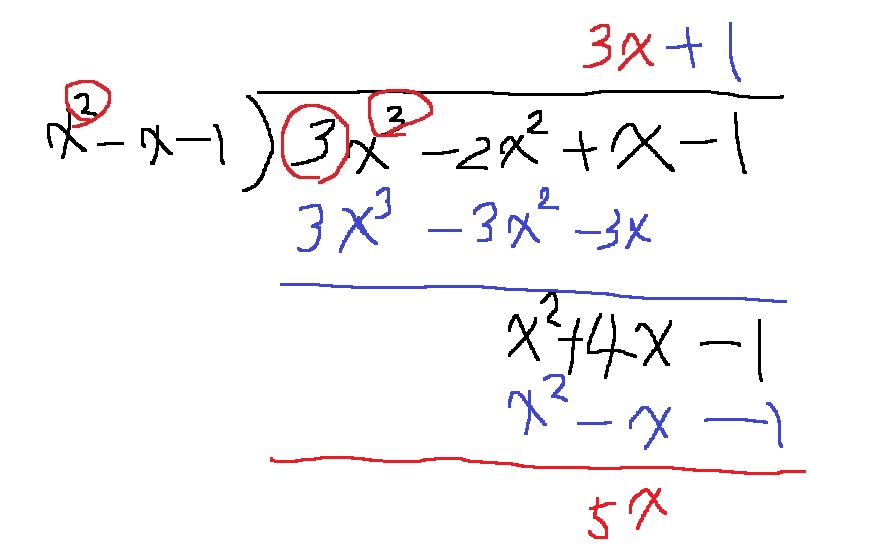
그러면 f(x)를 g(x)로 나눈 몫은 3x+1이고 나머지는 5x가 된다.
이 과정을 코드로 구현하면 다음과 같다.
#negative mod
def negative_mod(x,mod):
if x < 0:
return (x+mod)%mod
else:
return x%mod
#naive polynomial division
#a/b
def divide(a,b,mod):
q = [0]*(len(a)-len(b)+1) #몫
for i in range(len(q)-1,-1,-1):
#몫의 최고차항을 결정
q[i] = a[i+len(b)-1]//b[-1]
for j in range(len(b)-1,-1,-1):
#몫의 최고차항과 b의 항을 차례대로 곱하면서 a에 빼준다
a[i+j] -= (q[i]*b[j])
a[i+j] = negative_mod(a[i+j],mod) #값이 음수 일 수 있음
#나머지 차수 재조정
while a:
x = a.pop()
if x != 0:
a.append(x)
break
return q,a #몫,나머지
a = [-1,1,-2,3]
b = [-1,-1,1]
print(divide(a,b,10**9+7))
([1, 3], [0, 5])
나눗셈 같은 경우, mod 연산을 할려면 계수를 빼다보니 음수가 될 수 있는데, 음수에 대한 mod 연산을 해줘야한다.
음수에 대한 mod 연산은 간단한데, 그냥 x + mod를 mod로 나눠주면 된다.
제대로 된건지 모르겠네..
'대수학' 카테고리의 다른 글
| 컴퓨터가 실수를 연분수 표현(continued fraction)으로 나타내는 방법 (0) | 2023.09.20 |
|---|---|
| Fast Fourier Transform을 이용한 빠른 다항식 곱셈 공부하기 (0) | 2023.08.29 |
| 키타마사 법(kitamasa method, きたまさ法)에 대한 공부 (0) | 2023.08.27 |

