1. 두 다항식의 곱셈
다항식 $f(x) = a_{0}x^{0} + a_{1}x^{1} + ... + a_{n-1}x^{n-1}$과 $g(x) = b_{0}x^{0} + b_{1}x^{1} + ... + b_{n-1}x^{n-1}$의 곱셈은..
$f(x)g(x) = a_{0}b_{0}x^{0} + (b_{0}a_{1} + a_{1}b_{0})x^{1} + ... + a_{n-1}b_{n-1}x^{2n-2}$로 나타날 것이다.
다항식을 각각 계수만을 가진 길이가 n인 벡터 A = [a0,a1,...,an-1], B = [b0, b1, ... , bn-1]로 나타낸다고 할때,
두 다항식의 곱셈은 길이가 2n-1인 벡터 C = [c0,c1,...,c(2n-2)]로 나타나며,
$$c_{i} = \sum_{j=0}^{i}a_{j}b_{i-j} = a_{0}b_{i} + a_{1}b_{i-1} + ... + a_{i}b_{0}$$
각 벡터 A,B를 순회해서 구하는 $O(N^{2})$에 대해 구현가능한데..
https://deepdata.tistory.com/981
다항식의 곱셈과 나눗셈 기본 컴퓨터 구현 방법 배우기
1. 다항식의 곱셈 두 다항식의 곱셈은 구현하는 방법이 많이 있지만... 당장은 어려우니 일단 $O(k^{2})$으로 naive하게 구현 해보자. 다항식은 각 항의 계수를 배열에 저장하면 되는데 $f(x) = 2x^{2} + x
deepdata.tistory.com
더 빠르게 $O(NlogN)$에 구하는 방법에 대해 알고싶다..
2. lagrange interpolation
서로 다른 n+1개의 점 $(x_{1},y_{1}), (x_{2},y_{2}), ... , (x_{n+1},y_{n+1})$에 대하여 이 점을 모두 지나는 n차 다항식은 유일하다.
만약 $x_{1}, x_{2}, ... , x_{n+1}$과 이에 대한 함숫값 $f(x_{1}), f(x_{2}), ... , f(x_{n+1})$을 안다면, n차 다항식 f(x)를 유일하게 하나로 결정시킬 수 있다는 정리.
n+1 = 2개의 점 (1,1)과 (2,3)을 지나는 다항함수 $f(x) = 2x - 1$과 $g(x) = x^{2} - x - 1$ 등등이 존재하며 무수히 많다.
하지만 차수가 가장 낮은 다항식은 n=1차 다항식 f(x) = 2x-1이며 유일하다.
3. polynomial representation
결국 n차 다항식은 2가지 방법으로 표현할 수 있다.
계수들의 합으로 표현하는 coefficient representation
$$f(x) = \sum_{i = 0}^{n} a_{i}x^{i}$$
lagrange interpolation에 의한 point-value representation
$$(x_{0}, f(x_{0})), (x_{1}, f(x_{1})), ... , (x_{n}, f(x_{n}))$$
4. discrete fourier transform
n개의 복소수 $w_{0}, w_{1}, ... , w_{n-1}$에 대하여 $f(w_{0}), f(w_{1}), ... , f(w_{n-1})$로 대응시키는 함수 f(x)를 말한다.
구체적으로 다음과 같이 정의되는 것 같다.
$$f(w_{k}) = \sum_{j = 0}^{n-1} w_{j}e^{\frac{-i2k\pi}{n}j}$$
반대로 함수 $f(w_{k})$로부터 $w_{k}$를 구하는 것을 inverse discrete fourier transform이라고 부른다.
$$w_{j} = \frac{1}{n} \sum_{k=0}^{n-1} f(w_{k})e^{\frac{i2k\pi}{n}j}$$
5. primitive n-th root of unity
$w^{n} = 1$을 만족시키는 복소수 $w$를 n-th root of unity라고 부른다.
오일러의 공식(euler's formula)은 허수 i와 실수 x에 대해 다음이 성립한다는 것이다.
$$e^{ix} = cosx + isinx$$
여기서 $x = \pi$이면, $sin(\pi) = 0, cos(\pi) = -1$이므로 $e^{i\pi} = -1$이다.
따라서 짝수번을 거듭제곱하느냐, 홀수번을 거듭제곱하느냐에 따라 1 아니면 -1이 되는데...
k = 0,1,2,...,n-1에 대하여.. $$e^{\frac{2k\pi}{n}i} = cos(\frac{2k\pi}{n}) + isin(\frac{2k\pi}{n})$$으로 정의하면, n제곱이 항상 1이 된다.
$e^{\frac{2k\pi}{n}i}$는.. 위의 discrete fourier transform에 나온 숫자랑 똑같이 생겼다.. 이제 뭔가 연결되는 것 같다
1) 특히 n보다 작은 자연수 m = 1,2,..,n-1에 대하여..
$w^{n} = 1$이지만 $w^{m} \neq 1$을 만족할때, primitive하다고 부른다.
2) 여기에 n이 소수이면 모든 n-th root of unity는 primitive라고 한다.
3) 여기서 중요한 관찰은 primitive n-th root of unity $z$에 대하여 적당히 k번 거듭제곱하면
$(z^{k}) = w$이고 $w^{n} = 1$만족하는 N개의 n-th root of unity를 얻을 수 있다.
4) 그리고 $z^{k} = w = e^{\frac{2k\pi}{n}i} = cos(\frac{2k\pi}{n}) + isin(\frac{2k\pi}{n})$이다.
또한 k 대신에 k + n/2를 넣으면 $e^{\frac{2(k+n/2)\pi}{n}i} = e^{\frac{(2k+n)\pi}{n}i} = e^{\frac{2k\pi}{n}i}e^{i\pi} = -e^{\frac{2k\pi}{n}i} = - z^{k}$이다.
6. divide and conquer
길이 n인 다항식을 n/2인 두 다항식으로 분할할 수 있다.
구체적으로 짝수차수항과 홀수차수항만을 모은다.
$$f(x) = a_{0} + a_{1}x + a_{2}x^{2} + ... + a_{n-1}x^{n-1} = (a_{0} + a_{2}x^{2} + ...) + (a_{1}x + a_{3}x^{3} + ...) = (a_{0} + a_{2}x^{2} + ... ) + x(a_{1} + a_{3}x^{2} + ... )$$
여기서 n이 짝수일때 $f_{even}(x) = a_{0} + a_{2}x + a_{4}x^{2} + ... + a_{n-2}x^{n/2 -1}$이라 하고
$f_{odd}(x) = a_{1} + a_{3}x + a_{5}x^{2} + ... + a_{n-1}x^{n/2 - 1}$이라 하자.
그러면 $$f(x) = f_{even}(x^{2}) + xf_{odd}(x^{2})$$
7. fast fourier transform
primitive n-th root of unity $w$에 대하여 함숫값 $f(w_{0}), f{w_{1}), ..., f(w_{n-1}), g(w_{0}), g(w_{1}), ..., g(w_{n-1})$을 모두 알아낼 수 있으면
두 다항식의 곱셈은 $h(x) = f(x)g(x)$이므로 $h(w_{k}) = f(w_{k})g(w_{k})$이므로 $h(w_{k})$를 모두 알아낼 수 있다.
#DFT로 모든 f(w)를 구하는 함수
def dft(f,w):
n = len(f) #2의 거듭제곱으로 맞춰져있음
if n == 1:
return
#f의 크기를 절반씩 줄여나감
#n >> 1 = n//2
odd = [0]*(n>>1)
even = [0]*(n>>1)
#줄여나간 위치에 맞는 계수를 넣는다
#f = a0 + a1x + a2x^2 + a3x^3 + a4x^4 + ...
#f = (a0 + a2x^2 + a4x^4 + ...) + (a1x + a3x^3 + a5x^5 + ...)
#짝수 홀수 다항식을 관찰해보면..
# 0번 > 0//2 = 0번, 2번 > 2//2 = 1번, 4번 >> 4//2 = 2번,...
# 1번 > 1//2 = 0번, 3번 > 3//2 = 1번, 5번 >> 5//2 = 2번,...
#절반 위치로 계수가 이동함을 확인할 수 있다
for i in range(n):
if i & 1:
odd[i >> 1] = f[i]
else:
even[i >> 1] = f[i]
#다항식을 계속해서 분할하고.. 위에 보면 n == 1이면 return(분할할 수 없을때까지 분할)
#w^2을 넣는 이유는 f(x) = f_even(x^2) + xf_odd(x^2)이라서..
dft(even,w*w)
dft(odd,w*w)
#현재 크기에서 모든 w에 대해 f(w)를 구함
#f(w) = f_even(w^2) + w*f_odd(w^2)
#f(-w) = f_even(w^2) -w * f_odd(w^2)
#위에서 w*w를 넣어 분할했기 때문에, even[i],odd[i]에는 w_pow^2이 들어가있다
w_pow = 1
for i in range(n//2):
f[i] = even[i] + w_pow * odd[i] #w = x_i
f[i+n//2] = even[i] - w_pow * odd[i] #-w = x_i+n/2, 대칭관계에 있음
w_pow = w_pow * w
구현은 두 다항식 f,g의 차수가 $2^{k} - 1$ 형태라는 걸 가정하고 있다.
실제로 그렇지 않다면 계수가 0인 항을 추가해서 맞춰줘야한다고함
또한 마지막 반복문은 다음 원리에 입각하고 있다고 한다
두 복소수 w와 -w에 대하여 $f(x) = f_{even}(x^{2}) + xf_{odd}(x^{2})$이므로
$$f(w) = f_{even}(w^{2}) + wf_{odd}(w^{2})$$
$$f(-w) = f_{even}(w^{2}) -wf_{odd}(w^{2})$$
그런데 $w = e^{\frac{2k\pi}{n}i}$이면 $-w = e^{\frac{2(k+n/2)\pi}{n}i}$이다.
그래서 n/2개의 $f(w_{k})$를 구한다면 나머지 n/2개의 $f(w_{k+n/2})$를 바로 구할 수 있게 된다.
8. inverse fourier transform
두 다항식의 $f(w_{0}), f(w_{1}), ... f(w_{n-1}), g(w_{0}), g(w_{1}),..., g(w_{n-1})$을 위의 DFT로 모두 찾았고
대응하는 값들끼리 곱하면 h(x) = f(x)g(x)이므로 $h(w_{0}), h(w_{1}), ... , h(w_{n-1})$을 구할 수 있다.
이로부터 inverse transform을 수행하여 h(x)의 모든 계수를 얻는다.
증명이 조금 까다로운데..
역행렬을 만들어서 풀면 계수가 나온다고 하고

구체적으로 위에서 제시한 fourier transform 식을 보면 w 대신에 $w^{-1}$을 넣고,
$h(w_{0}), h(w_{1}), ... , h(w_{n-1})$을 계수로 한 discrete fourier transform을 수행하여, 각각을 n으로 나누면 된다고 한다.
#f,g를 곱하는 함수
def multiply(f,g):
n = 1
#f,g의 크기를 2의 거듭제곱으로 맞춘다
while n <= len(f) or n <= len(g):
n <<= 1
n <<= 1
#f,g의 크기가 2의 거듭제곱이 될때까지 고차항은 0으로 채움
while len(f) != n:
f.append(0)
while len(g) != n:
g.append(0)
h = [0]*n #두 다항식 f,g를 곱한 결과
#primitive n-th root of unity
#공식 cos(2pi/n) + isin(2pi/n)에 따라 그대로 구함
w = complex(cos(2*pi/n),sin(2*pi/n))
#f,g의 DFT를 구함
#모든 f(w), g(w)를 구한다
dft(f,w)
dft(g,w)
#h=fg이므로 모든 h(w)를 구함
for i in range(n):
h[i] = f[i]*g[i]
#inverse transform
#두 다항식의 곱 h의 계수를 구함
#1. 켤레복소수 w로 바꾸고 DFT를 구한다
dft(h,w.conjugate())
#2. 구해진 DFT를 n으로 나눈다.
for i in range(n):
h[i] /= n
h[i] = int(round(h[i].real)) #계수를 정수로 얻고 싶은 경우
return h
9. 연습문제
1067번: 이동
N개의 수가 있는 X와 Y가 있다. 이때 X나 Y를 순환 이동시킬 수 있다. 순환 이동이란 마지막 원소를 제거하고 그 수를 맨 앞으로 다시 삽입하는 것을 말한다. 예를 들어, {1, 2, 3}을 순환 이동시키면
www.acmicpc.net
10. 풀이
연습문제라곤 하지만... 생각보다 어렵다
구하고자 하는건 모든 가능한 convolution $\sum_{i,j} a_{i}b_{j}$중 최댓값을 구해야한다.
1) 근데 단순히 다항식으로 만들어서 곱하면..
$(a_{1}x+a_{2})(b_{1}x+b_{2}) = (a_{1}b_{1})x^{2} + (a_{2}b_{1}+b_{2}a_{1})x + a_{2}b_{2}$
그러면 x의 계수만 convolution이 되는데... 문제는 모든 convolution이 나오는것도 아니다.
항 수가 2개면 $a_{1}b_{1}+a_{2}b_{2}, a_{1}b_{2} + a_{2}b_{1}$이 있어야하는데
단순히 곱하면 $a_{2}b_{1} + a_{1}b_{2}$만 나오게 된다.
2) 두 다항식을 곱했을때 계수의 형태는 서로 반대방향으로 곱한 형태를 보인다.
$f(x) = a_{0}x^{0} + a_{1}x^{1} + ... + a_{n-1}x^{n-1}$이고 $g(x) = b_{0}x^{0} + b_{1}x^{1} + ... + b_{n-1}x^{n-1}$이라고 하자.
h(x) = f(x)g(x)의 계수 $c_{i}$는..
$$c_{i} = \sum_{j = 0}^{i} a_{j}b_{i-j} = a_{0}b_{i} + a_{1}b_{i-1} + ... + a_{i}b_{0}, i = 0,1,...,2n-2$$이라고 했다.

3) 그래서 모든 convolution을 얻기 위해 한쪽의 계수 배열을 2배로 늘린다.
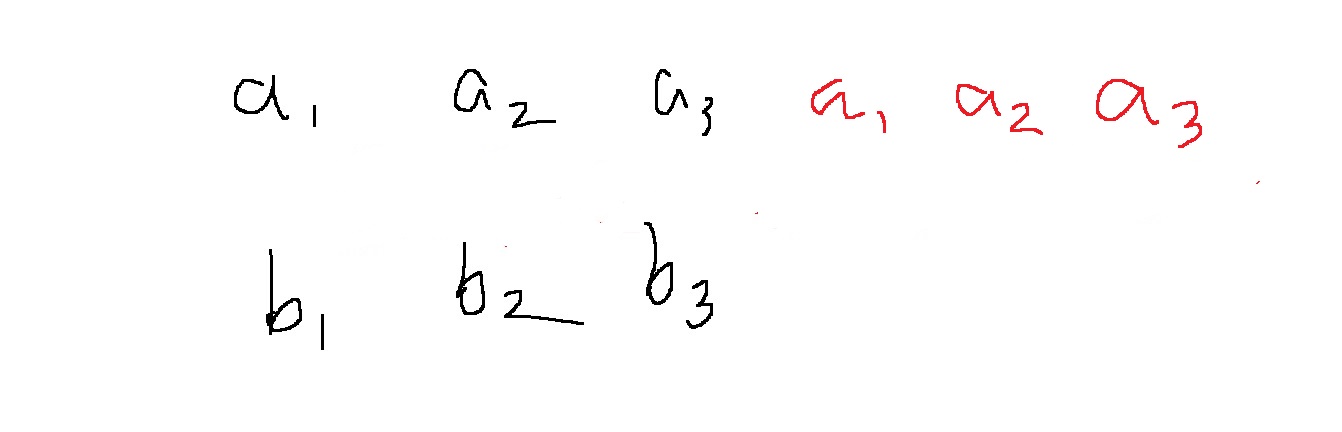
이 상태에서 $f(x) = a_{1} + a_{2}x^{1} + a_{3}x^{2} + a_{1}x^{3} + a_{2}x^{4} + a_{3}x^{5}$와 $g(x) = b_{1} + b_{2}x + b_{3}x^{2}$을 곱해서 만들어보면...
$a_{1}b_{3}+a_{2}b_{2} + a_{3}b_{1}$

이게 애초부터 불가능한 상황임
[a1,a2,a3]와 [b3,b2,b1]이 convolution되어야하는데, [b1,b2,b3]를 shift해서 [b3,b1,b2]는 만들어져도, [b3,b2,b1]은 나오지 않는다
그러니까 이후로는 [a1,a2,a3]를 한칸씩 shift하더라도 불가능한 경우만 나온다.
$a_{1}b_{1}+a_{3}b_{2}+a_{2}b_{3}$
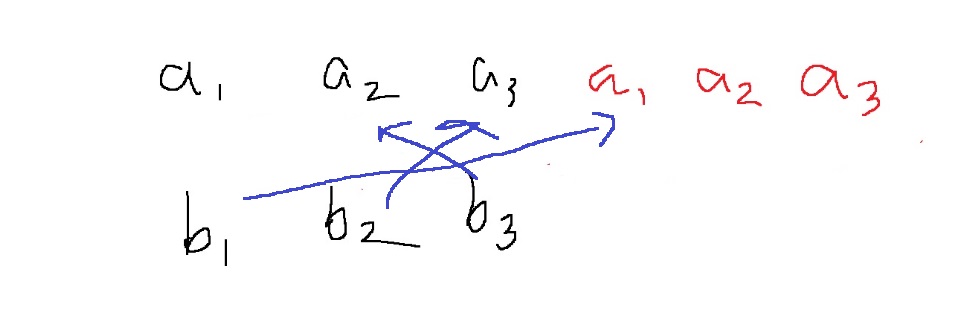
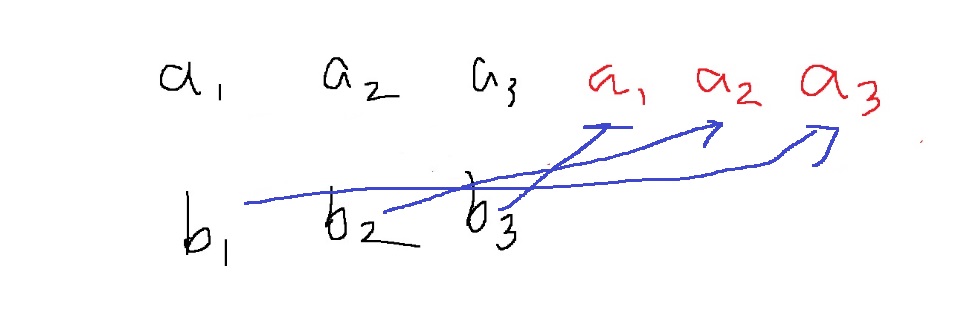
$a_{2}b_{1}+a_{1}b_{2}+a_{3}b_{3}$

$a_{3}b_{1} + a_{2}b_{2} + a_{1}b_{3}$
-------------------------------------------------------------------------------------------------------
근데 구해야하는 값은
$a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$
$a_{1}b_{3} + a_{2}b_{1}+ a_{3}b_{2}$
$a_{1}b_{2} + a_{2}b_{3} + a_{3}b_{1}$
위와 비교해보면 알겠지만... 미묘하게 다르고 일치하는게 하나도 없음..
다항식끼리 곱하면 계수끼리 역순으로 곱해져서 신기하게 다르더라고
4) 그래서 두번째 다항식의 계수는 역순으로 배치함

이러면 역으로 배치했으니까 두 다항식을 곱하면
계수 $c_{i} = \sum_{j = 0}^{i} a_{j}b_{j} = a_{1}b_{1} + a_{2}b_{2} + ... +a_{i}b_{i}$형태로 나올 것이다
$a_{3}b_{3} + a_{2}b_{2} + a_{1}b_{1}$
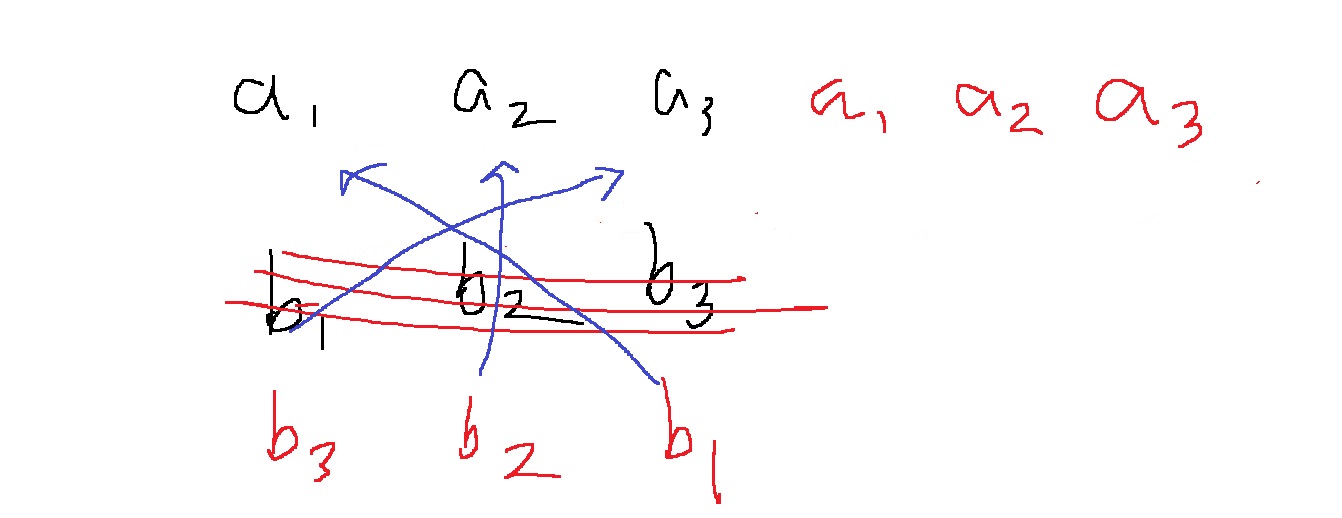
처음부터 [a1,a2,a3]와 [b1,b2,b3]의 convolution이므로
다음부터 [a1,a2,a3]를 한칸씩 shift해서 올바른 값을 얻을 수 있게 된다
$a_{1}b_{3} + a_{3}b_{2} + a_{2}b_{1}$

자세히 보면 바로 이전 [a1,a2,a3]를 shift한 [a2,a3,a1]과 [b1,b2,b3]의 역순곱이 된다.
$a_{2}b_{3} + a_{1}b_{2} + a_{3}b_{1}$

역시 이전 [a2,a3,a1]을 shift한 [a3,a1,a2]와 [b1,b2,b3]의 역순곱이 된다.
$a_{3}b_{3} + a_{2}b_{2} + a_{1}b_{1}$
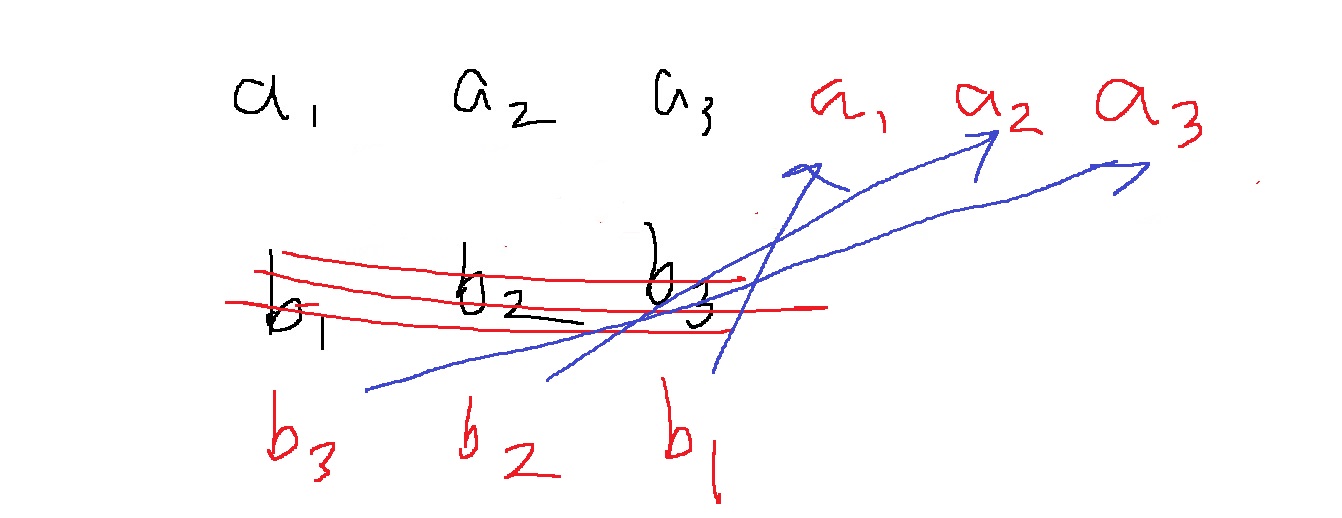
역시 이전 [a3,a1,a2]를 shift한 [a1,a2,a3]와 [b1,b2,b3]의 역순곱으로 처음과 동일해진다
따라서 처음에 X,Y를 받으면 X는 2배로 늘리고 Y는 역순으로 배치한다음 X와 Y를 FFT로 곱하여 계수를 얻는다.
최초 계수들이 0 이상의 양수이므로 X와 Y의 곱의 계수들은 곱해진 X,Y 계수들 수가 많을수록 클 것이다.
즉 위와 같은 경우
$a_{3}b_{3} + a_{2}b_{2} + a_{1}b_{1}$
$a_{1}b_{3} + a_{3}b_{2} + a_{2}b_{1}$
$a_{2}b_{3} + a_{1}b_{2} + a_{3}b_{1}$
$a_{3}b_{3} + a_{2}b_{2} + a_{1}b_{1}$
이 4가지 중 하나가 무조건 제일 큰 값이다.
따라서, FFT로 얻은 계수들에서 최댓값을 찾으면 된다.
from math import pi,cos,sin
from sys import stdin
#DFT로 모든 f(w)를 구하는 함수
def dft(f,w):
n = len(f) #2의 거듭제곱으로 맞춰져있음
if n == 1:
return
#f의 크기를 절반씩 줄여나감
#n >> 1 = n//2
odd = [0]*(n>>1)
even = [0]*(n>>1)
#줄여나간 위치에 맞는 계수를 넣는다
#f = a0 + a1x + a2x^2 + a3x^3 + a4x^4 + ...
#f = (a0 + a2x^2 + a4x^4 + ...) + (a1x + a3x^3 + a5x^5 + ...)
#짝수 홀수 다항식을 관찰해보면..
# 0번 > 0//2 = 0번, 2번 > 2//2 = 1번, 4번 >> 4//2 = 2번,...
# 1번 > 1//2 = 0번, 3번 > 3//2 = 1번, 5번 >> 5//2 = 2번,...
#절반 위치로 계수가 이동함을 확인할 수 있다
for i in range(n):
if i & 1:
odd[i >> 1] = f[i]
else:
even[i >> 1] = f[i]
#다항식을 계속해서 분할하고.. 위에 보면 n == 1이면 return(분할할 수 없을때까지 분할)
#w^2을 넣는 이유는 f(x) = f_even(x^2) + xf_odd(x^2)이라서..
dft(even,w*w)
dft(odd,w*w)
#현재 크기에서 모든 w에 대해 f(w)를 구함
#f(w) = f_even(w^2) + w*f_odd(w^2)
#f(-w) = f_even(w^2) -w * f_odd(w^2)
#위에서 w*w를 넣어 분할했기 때문에, even[i],odd[i]에는 w_pow^2이 들어가있다
w_pow = 1
for i in range(n//2):
f[i] = even[i] + w_pow * odd[i] #w = x_i
f[i+n//2] = even[i] - w_pow * odd[i] #-w = x_i+n/2, 대칭관계에 있음
w_pow = w_pow * w
#f,g를 곱하는 함수
def multiply(f,g):
n = 1
#f,g의 크기를 2의 거듭제곱으로 맞춘다
while n <= len(f) or n <= len(g):
n <<= 1
n <<= 1
#f,g의 크기가 2의 거듭제곱이 될때까지 고차항은 0으로 채움
while len(f) != n:
f.append(0)
while len(g) != n:
g.append(0)
h = [0]*n #두 다항식 f,g를 곱한 결과
#primitive n-th root of unity
#공식 cos(2pi/n) + isin(2pi/n)에 따라 그대로 구함
w = complex(cos(2*pi/n),sin(2*pi/n))
#f,g의 DFT를 구함
#모든 f(w), g(w)를 구한다
dft(f,w)
dft(g,w)
#h=fg이므로 모든 h(w)를 구함
for i in range(n):
h[i] = f[i]*g[i]
#inverse transform
#두 다항식의 곱 h의 계수를 구함
#1. 켤레복소수 w로 바꾸고 DFT를 구한다
dft(h,w.conjugate())
#2. 구해진 DFT를 n으로 나눈다.
for i in range(n):
h[i] /= n
h[i] = int(round(h[i].real)) #계수를 정수로 얻고 싶은 경우
return h
n = int(stdin.readline())
x = list(map(int,stdin.readline().split()))
y = list(map(int,stdin.readline().split()))
x += x
z = multiply(x,y[::-1])
print(max(z))
11. 비재귀 구현
DFT 함수가 재귀함수로 되어있는데, 비재귀로 만들 수 있으면 속도에서 이득을 볼 수 있다.
bit를 뒤집는 방법을 쓰는 것 같은데 무슨 말인지 모르겠다 (이해할려고 노력도 안했지만...)
코드가 직관적이지 않지만 재귀보다 조금 더 빠르긴하다..
이건 걍 만들어진거 가져다 쓰는게..
from math import pi,sin,cos
def bit_reverse(f,n):
j = 0
for i in range(1,n):
bit = n >> 1
while j >= bit:
j -= bit
bit >>= 1
j += bit
if i < j:
f[i],f[j] = f[j],f[i]
def dft(f,inverse = False):
n = len(f)
bit_reverse(f,n)
roots = [0]*(n//2)
if inverse == False:
for i in range(n//2):
roots[i] = complex(cos(2*i*pi/n),sin(2*i*pi/n))
else:
for i in range(n//2):
roots[i] = complex(cos(2*i*pi/n),-sin(2*i*pi/n))
i = 1
while i <= n:
step = n//i
for j in range(0,n,i):
for k in range(i//2):
u = f[j+k]
v = f[j+k+i//2] * roots[step*k]
f[j+k] = u+v
f[j+k+i//2] = u - v
i *= 2
def multiply(f,g):
n = 1
#f,g의 크기를 2의 거듭제곱으로 맞춘다
while n <= len(f) or n <= len(g):
n <<= 1
n <<= 1
while len(f) != n:
f.append(0)
while len(g) != n:
g.append(0)
h = [0]*n
dft(f)
dft(g)
for i in range(n):
h[i] = f[i]*g[i]
dft(h,True)
for i in range(n):
h[i] /= n
h[i] = int(round(h[i].real))
return h
12. 되짚어보기..
1) 위의 FFT 알고리즘은 cooley - tukey 알고리즘이고 빠른 곱셈 알고리즘으로 카라츠바 알고리즘도 있고 많이 있는듯 하다
2) 두 다항식 계수 배열을 2의 거듭제곱으로 가정하는 이유는 분할정복시 절반으로 나누기 편하니까? 그런듯하다
그리고 cooley - tukey 알고리즘이 애초에 배열 크기가 2의 거듭제곱이라고 가정한다고 본것 같은데
곱한 결과는 곱한 차수보다 크게 나오니까 고차항에서 계수가 0인 부분은 빼고 최초로 0이 아닌 부분부터 사용하면 될듯?
3) 흐름을 되짚어보면..
다항식 n개의 서로 다른 점 x에 대해 함숫값 f(x)를 안다면 n-1차 다항식 f(x)를 유일하게 결정지을 수 있다(라그랑주 보간법)
>> h(x) = f(x)g(x)니까 2n-3개의 f(x)g(x)를 모두 알아낸다면 2n-2차 다항식 h(x)를 유일하게 결정지을 수 있다.
>> f(x), g(x)를 알고 있으니까 적당한 x를 이용해서 f(x)g(x)를 구하고 h(x)를 구하면 되겠네
이건 $O(Nlog^{2}N)$정도로 동작하는 라그랑주 보간법이 있는 것 같은데.. 이건 좀 찾아봐야겠다
>> 라그랑주 보간법은 모르니까 아무 값이나 넣어서 구하면 함숫값이야 O(N)에 구하더라도 함숫값으로부터 계수를 구하는 과정이 안됨
>> 하지만 fourier transform 식을 이용하면 가능하다 이거지
fourier transform 식과 inverse fourier transform 식을 보면 식에 나오는 복소수 $w = e^{2\pi/n}i}$를 쓰면 w >> f(w)로부터 f(w) >> w를 구하기가 쉽다
w 대신 w^{-1}를 쓰고 fourier transform을 한 다음에 n으로 나눠주면 되거든
또한 w의 거듭제곱이 절반씩 서로 대칭에 있는 성질도 있음
.. 여기서 두 다항식의 곱셈과 복소수 w, fourier transform이 연결됨
>> w의 성질과 다항식 f를 절반으로 나눌 수 있다는 성질을 이용해서
f(w)들을 구하는데 2의 거듭제곱 크기로 만든 f를 절반씩 조절해서 분할정복으로 모든 f(w)를 빠르게 구할 수 있다.
이 정도 느낌을 가져가고 FFT는 필요할때마다 가져다 쓰는게 제일 좋을듯..?
모듈러 연산을 해야되는데 지금 내용은 그런게 없어서 실전성 있는지는 모르겠고
내 수준에서 볼만한 코딩 시험에서 쓸일도 없을듯
참고
https://en.wikipedia.org/wiki/Discrete_Fourier_transform
Discrete Fourier transform - Wikipedia
From Wikipedia, the free encyclopedia Type of Fourier transform in discrete mathematics Fig 1: Relationship between the (continuous) Fourier transform and the discrete Fourier transform. Left column: A continuous function (top) and its Fourier transform (b
en.wikipedia.org
https://namu.wiki/w/%EC%9D%B4%EC%82%B0%20%ED%91%B8%EB%A6%AC%EC%97%90%20%EB%B3%80%ED%99%98
이산 푸리에 변환 - 나무위키
이산 푸리에 변환은 다음과 같은 식으로써 정의된다. Discrete Fourier Transform (DFT) X[k]=∑n=0N−1x[n]e−i2πknN\displaystyle X[k]= \sum_{n=0}^{N-1} x[n] e^{-i\frac{2 \pi k n}{N}} \quad \quad X[k]=n=0∑N−1x[n]e−iN2πkn Inv
namu.wiki
https://en.wikipedia.org/wiki/Root_of_unity
Root of unity - Wikipedia
From Wikipedia, the free encyclopedia Number that has an integer power equal to 1 The 5th roots of unity (blue points) in the complex plane In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when ra
en.wikipedia.org
https://justicehui.github.io/hard-algorithm/2019/09/04/FFT/
FFT in PS
목차 convolution 다항식의 표현 DFT n-th root of unity DFT와 n-th root of unity FFT IDFT 예제) 큰 수 곱셈
justicehui.github.io
https://namnamseo.tistory.com/entry/FFT-in-competitive-programming
FFT in competitive programming
다항식 찾기 (n+1)개의 점, 즉 $(x_i, y_i)$의 순서쌍이 (n+1)개 주어지면, 이 n개의 점을 모두 지나는 다항식을 하나 찾을 수 있다. 즉 $P(x_i) = y_i$를 모두 만족하는 $P(x)$를 찾을 수 있다. (일단 각각의 $x
namnamseo.tistory.com
https://speakerdeck.com/wookayin/fast-fourier-transform-algorithm
Fast Fourier Transform Algorithm
A Introduction to FFT (Fast Fourier Transform) Algorithm with its application in competitive programming. This talk was given in the 2012 SNUPS (Seoul National University Problem Solving Group) Algorithm seminar.
speakerdeck.com
'대수학' 카테고리의 다른 글
| 컴퓨터가 실수를 연분수 표현(continued fraction)으로 나타내는 방법 (0) | 2023.09.20 |
|---|---|
| 키타마사 법(kitamasa method, きたまさ法)에 대한 공부 (0) | 2023.08.27 |
| 다항식의 곱셈과 나눗셈 기본 컴퓨터 구현 방법 배우기 (0) | 2023.08.26 |

