1. 중복조합
n종류가 있을 때, k개를 선택하는데 종류의 중복을 허용해서 선택하는 방법의 수를 구하고 싶다.
예를 들어 a,b,c 3개의 문자 중 5개를 중복을 허용해서 선택한다면
(a,a,a,a,a)
(a,a,a,a,b)
(a,a,a,b,c)
....
(b,b,b,c,c) 등등이 있다.
이러한 방법의 수를 어떻게 찾을 수 있을까?
5개의 빈칸에 a,b,c를 결정하면 되는데 2개의 칸막이를 이용해서 다음과 같이 구별하는 방법의 수로 이해할 수 있다
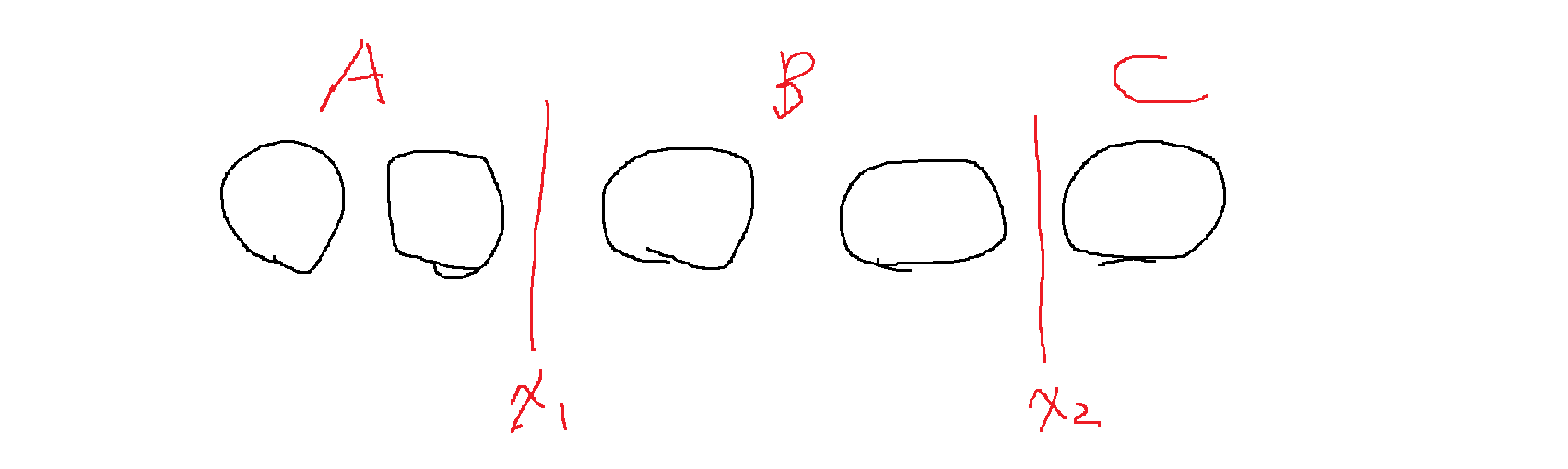
x1,x2 2개의 칸막이를 적당히 옮겨서 첫번째 영역에는 a를 전부 넣고, 두번째 영역에는 b를 전부 넣고
세번째 영역에는 c를 전부 넣는다.
n종류를 구분할려면 필요한 칸막이의 개수는? n-1개이다.
1개를 놓으면 2 영역이 생기고
2개를 놓으면 3 영역이 생기고
3개를 놓으면 4 영역이 생기고
...
n-1개를 놓으면 n 영역이 생기니까
그러면 총 필요한 자리의 수는 k + (n-1)개이고, 여기서 n-1개의 자리를 뽑아 칸막이를 배치하면 된다

n종류 중 k개를 중복을 허용해서 선택하는 중복조합의 수는 $nHk$로 표현하고
이는 위에서 보인 것처럼 $k+n-1Cn-1$과 같다
$nCr = nCn-r$이므로, $$nHk = k+n-1Cn-1 = k+n-1Ck$$
2. 응용 - 음이 아닌 정수해의 개수
3개의 음이 아닌 정수 x,y,z에 대하여 x + y + z = 10을 만족하는 (x,y,z)의 개수는?
이는 위의 중복조합의 상황을 생각하면
10개 중에서 3개를 중복을 허용해서 선택하는 경우의 수와 같다

따라서 일반적으로 확장하면 음이 아닌 정수 $x_{i} >= 0$에 대하여
$x_{1} + x_{2} + ... + x_{n} = k$를 만족하는 (x1,x2,..,xn)의 개수는
n종류에서 k개를 뽑는 중복조합의 수 nHk와 같다.
3. 확장 - 정수해의 개수
이번엔 x + y + z = 10을 만족하는 (x,y,z)의 개수를 구하고 싶은데 y,z가 0 이상의 정수이지만 x가 1 이상의 정수인 경우를 찾고 싶다.
그렇다면 x를 무조건 1개를 뽑는다.
그러면 x + y + z = 9를 만족하는 (x,y,z)의 경우에 x 하나만 추가하면 반드시 x는 1이상이 된다.
일반적으로 $x_{1} + x_{2} + ... + x_{n} = k, x_{i} >= r$을 만족하는 (x1,x2,..,xn)의 개수를 구하고 싶다면...
$x_{i}$를 먼저 r개를 뽑으면 된다.
총 n종류에 대해 r개를 일단 뽑으면 양변에 nr을 빼면 되므로
$x_{1} + x_{2} + ... + x_{n} = k - nr, x_{i} >= 0$을 만족하는 (x1,x2,..,xn)의 개수와 같고
그러므로 n종류에서 k-nr개를 뽑는 중복조합의 수 nH(k-nr)과 같다.
'조합론' 카테고리의 다른 글
| 다항식의 곱으로 구하는 복수순열1 - 주어진 개수의 알파벳들만으로 만들 수 있는 문자열의 개수 (0) | 2024.06.18 |
|---|---|
| 원형테이블에 앉은 n명의 사람 중 서로 인접하지 않은 k명의 사람을 뽑는 방법 (0) | 2024.06.07 |
| 적어도 1명 이상이 자기 자신 것을 그대로 가져갈 확률은?(교란순열의 수렴) (0) | 2024.05.08 |
| DP가 불가능할 때 특정 위치 (x,y)로 이동하는 경우의 수를 구하는 다른 방법 (0) | 2024.04.05 |
| 주어진 순열의 다음 순열을 효과적으로 찾는 방법(next permutation, prev_permutation) (0) | 2024.03.12 |

