1. 일렬로 앉은 경우
먼저 n명의 사람이 일렬로 앉아있다고 생각해보자.
a1, a2, a3, ... , an이 일렬로 앉아있고, 여기서 서로 인접하지 않게 b1,b2,...,bk를 선택한다고 생각해보자.

b1,b2,...,bk가 서로 인접하지 않다는 것은 무슨 뜻일까?
먼저 선택한 k명 b1,b2,...,bk 사이의 선택받지 못한 x1,x2,x3,..,xk,xk+1에 대해, x1+x2+...+xk+1 = n-k이다.
왜냐하면 n명중 k명 b1,b2,..,bk를 선택하고 나서 남은 사람은 n-k명이니까

여기서 b1,b2,..,bk가 서로 인접하지 않을려면 그 사이에는 사람이 최소 1명이상 있어야한다.
즉, x2,x3,...,xk는 최소 1 이상이고 x1,xk+1은 0이상이다.
그러므로 구하고자 하는 경우의 수는...
$$x_{1} + x_{2} + ... + x_{k+1} = n-k, x_{1} >= 0, x_{k+1} >= 0, x_{i} >= 1, i = 2,3,..,k$$를 만족하는 정수해 (x1,x2,..,xk+1)의 개수이다.
이러한 정수해 (x1,x2,..,xk+1)만 결정한다면, 나머지에서 k명을 선택하면 되기 때문이다.
2. 정수해의 개수
https://deepdata.tistory.com/1260
n명 중 k명을 중복해서 선택하는 중복조합의 수 이해하기
1. 중복조합 n종류가 있을 때, k개를 선택하는데 종류의 중복을 허용해서 선택하는 방법의 수를 구하고 싶다. 예를 들어 a,b,c 3개의 문자 중 5개를 중복을 허용해서 선택한다면 (a,a,a,a,a) (a,a,a,a
deepdata.tistory.com
$x_{1} + x_{2} + ... + x_{k+1} = n-k, x_{1} >= 0, x_{k+1} >= 0, x_{i} >= 1, i = 2,3,..,k$를 만족하는 정수해 (x1,x2,..,xk+1)의 개수는?
$x_{2}, x_{3}, ... , x_{k}$가 최소 1 이상이어야 하므로, 먼저 k-1개를 미리 뽑으면
$x_{1} + x_{2} + ... + x_{k+1} = n-k-(k-1) = n-2k+1$을 만족하는 음이 아닌 정수 (x1,x2,..,xk+1)의 개수를 찾는 것과 같다.
이는 k+1개 중 n-2k+1개를 중복을 허용해서 뽑는 중복조합의 수 $k+1Hn-2k+1 = n-k+1Cn-2k+1 = n-k+1Ck$이다.
3. 원형으로 앉은 경우
하지만 문제는 n명의 사람이 원형으로 앉을 때이다.
일렬로 앉아있는 경우의 수 n-k+1Ck가지에서, 원형으로 앉았다고 생각했을 때, '인접하지 않아야하는 경우'에 위배되는 경우가 있다.
일렬로 앉아있는 경우의 수는 $x_{1} + x_{2} + ... + x_{k+1} = n-k, x_{1} >= 0, x_{k+1} >= 0, x_{i} >= 1, i = 2,3,..,k$에서
(x1,x2,..,xk+1)의 개수를 구한 것인데...
원형으로 앉았다고 생각해보자.

x2,x3,..,xk >= 1이므로 상관없고 x1 = 0, xk+1 = 0인 경우 b1과 bk가 서로 붙어버리므로
원형으로 앉았을때 b1,bk가 서로 인접하게 된다
x1,xk+1중 하나가 1이면, b1,bk가 서로 붙지 않으므로 조건에 위배되지 않는다.
따라서 (일렬로 앉은 경우에서 서로 인접하지 않은 경우) - (x1 = 0, xk+1 = 0인 경우)가 구하고자 하는 경우가 된다.
x1 = 0, xk+1 = 0인 경우는 $x_{2} + x_{3} + ... + x_{k} = n-k, x_{i} >= 1, i = 2,3,..,k$인 (0,x2,..,xk,0)의 개수를 찾는 것이다.
이는 $x_{2} + ... + x_{k} = n-k - (k-1)$을 만족하는 음이 아닌 정수해의 개수이므로...
k-1Hn-2k+1 = n-k-1Cn-2k+1 = n-k-1Ck-2가지
따라서 원형으로 앉은 n명의 사람중 인접하지 않은 k명을 뽑는 방법의 수는... $(n-k-1Ck) - (n-k-1Ck-2)$가지
4. 다른 방법으로 접근
그냥 원형으로 앉았을 때를 생각해보면 먼저 b1을 고정시켰을때
$x_{1} + x_{2} + ... + x_{k} = n-k, x_{i} >= 1, i = 1,2,3...,k$를 만족하는 (x1,x2,..,xk)의 개수를 찾아야한다.
이는 kHn-2k = n-k-1Cn-2k = n-k-1Ck-1가지
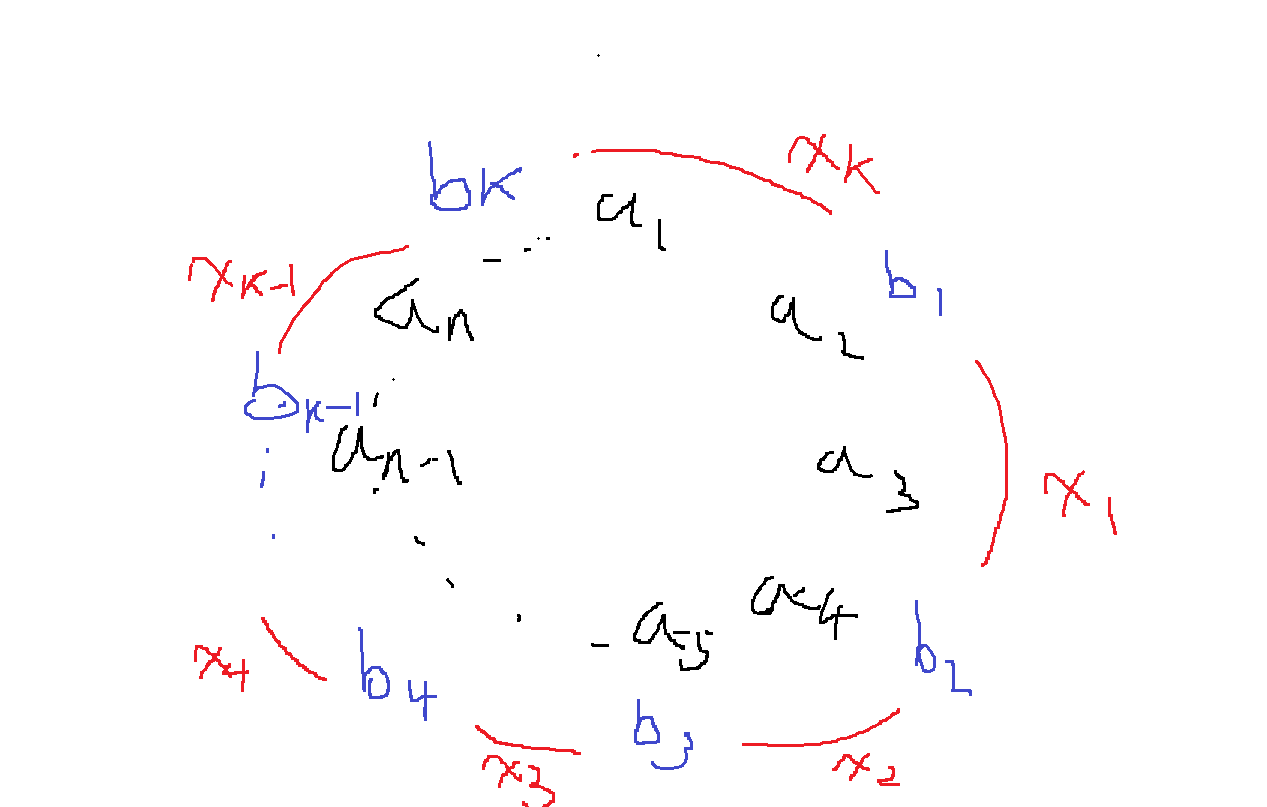
그러면 b1을 고정시키는 방법의 수는... a1,a2,..,an중 1가지를 고르는 방법의 수와 같으므로 nC1 = n가지
n * n-k-1Ck-1가지로 k명을 원형으로 앉히는 방법의 수를 찾았는데
원형으로 앉으므로, 첫번째 사람 b1이 어디에 앉든지간에, 나머지가 같으면 같은 경우이다.

예를 들어 x,y,z 3사람이 1,3,6에 앉든지 2,4,7에 앉든지 x,y,z는 같다는 것임
이러한 경우는 k명 b1,b2,..,bk가 선택되었을때, 첫번째 사람 b1이 k가지 앉을 수 있고 이들이 모두 같은 경우이므로...
전체 경우의 수를 k가지 나눠줘야한다.
원순열이랑 똑같은 원리임
따라서 전체 구하고자 하는 경우의 수는 $n*n-k-1Ck-1//k$
5. 연습문제
위와 동일한 문제로 n가지 색이 원형으로 배열되어 있을 때, 서로 인접하지 않은 k개의 색을 고르는 방법의 수를 구하는 문제
#원형으로 배열된 n명의 색 중 인접하지 않은 k개의 색을 고르는 방법의 수
#일렬로 배열한 경우에서, 원형으로 앉았을 때 불가능한 경우를 제외
#일렬로 배열한 경우는 x1+x2+...+xk+1 = n-k, x1,xk+1 >= 0, x2,x3,..,xk >= 1인 정수해의 개수
#k+1Hn-2k+1 = n-k+1Ck
#여기서 원형으로 앉았을 때 불가능한 경우는 양 끝 x1 = 0, xk+1 = 0이면 b1,bk이 서로 붙어버리므로 불가능
#x2+...+xk = n-k인 1이상의 정수해의 개수
#k-1Hn-2k+1 = n-k-1Ck-2
n = int(input())
k = int(input())
f = [0]*(n+1)
f[0] = 1
mod = 10**9+3
for i in range(1,n+1):
f[i] = f[i-1] * i
v1 = f[n-k+1]//(f[k]*f[n-k+1-k])
v2 = f[n-k-1]//(f[k-2]*f[n-k-k+1])
print((v1 - v2) % mod)
혹은 바로 원형으로 앉혀서 구한다면...
#원형으로 배열된 n개의 색에서 서로 인접하지 않은 k개의 색을 고르는 방법
#b1을 고정하고 x1+x2+...+xk = n-k, xi >= 1인 정수해의 개수 kHn-2k = n-k-1Ck-1
#b1을 고정하는 방법의 수 nC1 = n
#n*n-k-1Ck-1가지에서 원형으로 배열된 b1,b2,..,bk의 경우 첫번째 사람이 k자리에 앉은 경우가 모두 같으므로
#k로 나눠줘야함
n = int(input())
k = int(input())
f = [0]*(n+1)
f[0] = 1
mod = 10**9+3
for i in range(1,n+1):
f[i] = f[i-1] * i
v = f[n-k-1]//(f[k-1]*f[n-k-k])
print((v*n//k) % mod)
'조합론' 카테고리의 다른 글
| 경기장 일렬 좌석에 앉을 때 사람을 지나치지 않고 전부 앉는 방법의 수 (0) | 2024.07.26 |
|---|---|
| 다항식의 곱으로 구하는 복수순열1 - 주어진 개수의 알파벳들만으로 만들 수 있는 문자열의 개수 (0) | 2024.06.18 |
| n명 중 k명을 중복해서 선택하는 중복조합의 수 이해하기 (0) | 2024.06.07 |
| 적어도 1명 이상이 자기 자신 것을 그대로 가져갈 확률은?(교란순열의 수렴) (0) | 2024.05.08 |
| DP가 불가능할 때 특정 위치 (x,y)로 이동하는 경우의 수를 구하는 다른 방법 (0) | 2024.04.05 |

