1. 방향도함수(directional derivate)
이변수함수 z = f(x,y)와 임의의 단위벡터(norm이 1인 벡터) u = (a,b)에 대하여...
벡터 u를 지나는 평면으로 z = f(x,y)를 잘랐을때 생기는 곡선 위 (x0,y0,z0)위에서의 접선의 기울기?
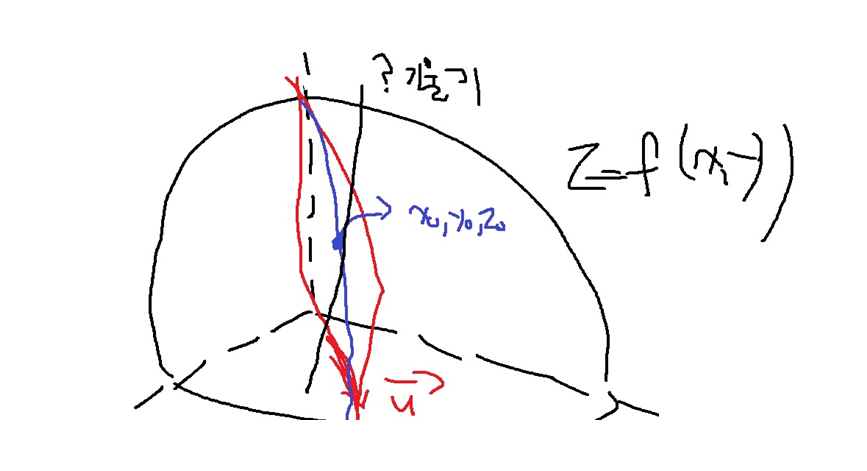
다음과 같이 정의되는 식을 u = (a,b)에 대한 방향도함수라고 부른다.

g(h) = f(x0 + ha, y0 + hb)라고 하자. h = 0이면 g(0) = f(x0,y0)이므로..
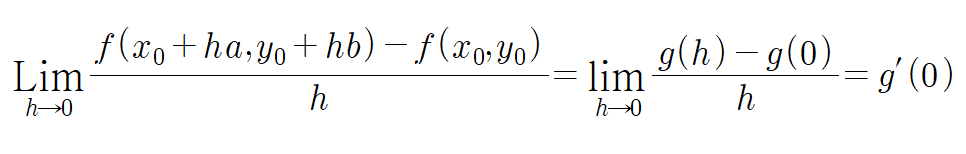
그런데 x(h) = x0 + ha, y(h) = y0 + hb라 하고 g(h) = f(x(h), y(h))라고 하자.
합성함수 미분법에 의하여... 다음과 같이 유도가능하다.
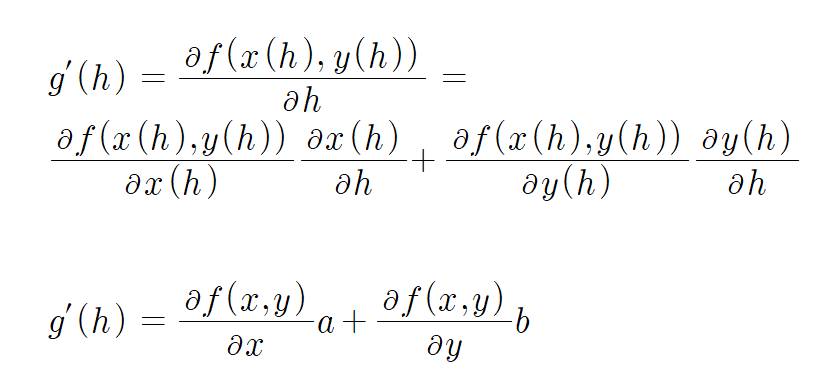
위 식에 h = 0을 넣으면 g'(0)이고 이는 방향도함수와 같으므로...
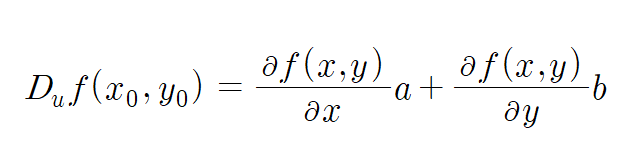
u = (a,b)이고 f(x,y)를 x로 편미분하고 y로 편미분하여 $(\frac{df(x,y)}{dx}, \frac{df(x,y)}{dy})$의 내적으로 나타낼 수 있다.

https://deepdata.tistory.com/127
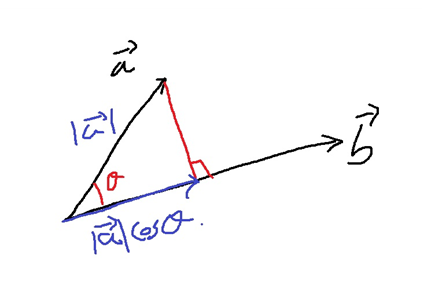
벡터의 내적의 기하학적 의미
1. 내적의 기하학적 의미 1-1) 정사영(projection) 위의 그림에서 벡터 a를 x의 정사영이라고 부른다 (projection) 1-2) 정사영의 길이 삼각함수 cos을 이용하여 위와 같이 정사영의 길이를 쉽게 구할 수 있
deepdata.tistory.com
두 벡터의 내적 a * b는 a와 b가 이루는 각 $\theta$에 대하여 |a||b|cos$\theta$로 구할 수 있다.
2. 그래디언트 벡터(gradient vector)
다음과 같이 유도된 방향도함수 공식

f(x,y)를 x,y로 각각 편미분하여 얻은 다음 벡터를 gradient vector라고 부른다

단위벡터 u의 크기는 1이므로 다음 그림과 같이 u에 대한 gradient vector를 u에 정사영시킨 벡터의 크기
|f|cos$\theta$는 방향도함수의 크기가 된다.
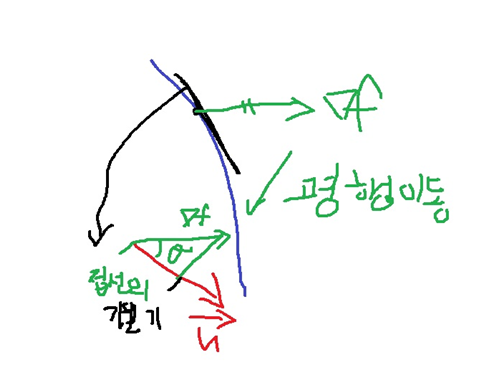
3. 방향도함수의 최대화
이변수함수 z = f(x,y)에서 단위벡터 u = (a,b) 방향으로 자른 곡선 위에서 접선의 기울기를 최대로 만드는 방법
방향도함수는 위에서 유도한대로
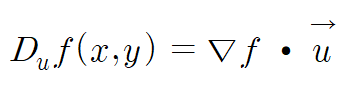
내적을 cos을 이용해서 나타내면.. u의 벡터 크기는 1이므로..

여기서 cos은 -1이상 1이하이므로

따라서 방향도함수의 최댓값은 cos = 1일 때, 그래디언트 벡터의 크기 |f|이다.
cos = 1이라는 것은 $\theta = 0$으로 두 벡터 u와 f가 방향이 일치할때이다.
최솟값은 cos = -1일 때이고 $\theta = 180$으로 두 벡터 u와 f의 방향이 서로 반대일때이다.
다변수함수 f(x)의 단위벡터 u 방향으로 자른 곡선에 대하여
접선의 기울기는 그래디언트 벡터 f와 방향 u의 내적(방향도함수의 크기)으로 얻어지며
최댓값은 그래디언트 벡터의 크기 |f|와 같다.

접선의 기울기가 최대일려면 방향벡터 u와 그래디언트 벡터 f의 방향이 일치할때이며,
이럴때 가장 빠르게 함숫값이 증가한다.
그리고 u와 f의 방향이 서로 반대일때 접선의 기울기가 음수로 가장 크며, 가장 빠르게 함숫값이 감소한다.
4. gradient descent와의 연결
위의 이유가 gradient descent에서 그래디언트 벡터의 방향이 가장 빠르게 함숫값이 감소하는 방향이다.
다변수함수 f의 방향도함수는 f에서 u 방향으로 자른 곡선의 접선의 기울기이다.
접선의 기울기는 f를 미분하여 얻은 변화율 f'
변화율은 함수 f의 함숫값의 변화 정도
방향도함수인 변화율 f'이 최대가 되는 것은 방향 u와 그래디언트 벡터 f의 방향이 일치할때이다.
즉 그래디언트 벡터 f의 방향으로 함숫값의 변화가 가장 빠르다.
반대로 그래디언트 벡터 f의 방향의 반대방향으로는 함수 f의 함숫값이 가장 빠르게 감소한다.
참고) 그래디언트 벡터의 기하학적 의미
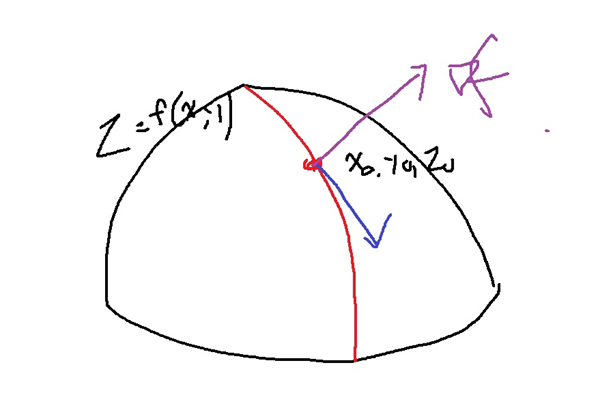
그래디언트 벡터 f의 방향은 다변수함수 f의 임의의 점에 대한 모든 접선의 방향을 나타내는 벡터(파란색)에 수직인 방향
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| hyperparameter 개념 간단하게 (0) | 2024.04.02 |
|---|---|
| 라그랑주 승수법 간단하게 (0) | 2024.03.01 |
| reproducibility를 위한 random seed (0) | 2023.12.11 |
| 구현하면서 배우는 weight initialization(가중치 초기화) 중요성 (0) | 2023.09.13 |
| 구현하면서 배우는 batch normalization에 대한 몇가지 핵심사항 (0) | 2023.09.13 |

