라그랑주 승수법은 제약조건이 있을 때 함수를 최대화, 최소화시키는 방법이다
최적화시키고자하는 함수 f(x,y)와 제약조건은 보통 g(x,y) = c 형태로 주어진다.
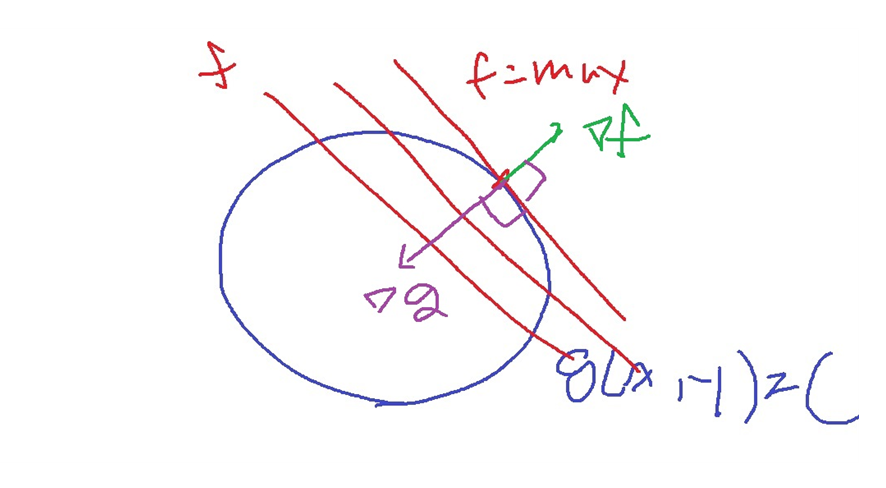
변하는 값은 함수 f(x,y)인데 이것을 변화시키다가 g(x,y) = c와 서로 접할때 함수 f가 최대가 되는 경우가 가장 쉬운 경우
https://deepdata.tistory.com/1115
gradient descent를 위한 gradient vector의 이론적 설명 간단하게
1. 방향도함수(directional derivate) 이변수함수 z = f(x,y)와 임의의 단위벡터(norm이 1인 벡터) u = (a,b)에 대하여... 벡터 u를 지나는 평면으로 z = f(x,y)를 잘랐을때 생기는 곡선 위 (x0,y0,z0)위에서의 접선의
deepdata.tistory.com
f와 g가 서로 접하는 경우는 무엇을 의미할까?
접점에서 접선의 방향을 나타내는 벡터들은 접점은 f,g 모두에 있는 점이니까 서로 동일하다.
그러므로 이것에 수직인 벡터들인 f와 g에서의 gradient vector(기하학적 의미 - 접선벡터에 수직)는
서로 방향이 동일하거나 서로 방향이 반대인 평행관계이다.
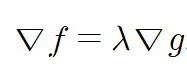
여기서 실수 $\lambda$는 라그랑주 승수라고 부른다.
이제 함수 f(x,y)의 최적화 문제는 $\bigtriangledown f = \lambda \bigtriangledown g$ 와 g(x,y) = c의 연립방정식의 해 (x,y)를 구하는 문제이다.
비슷하게 제약조건이 g,h로 여러개있다면?
$\bigtriangledown f = \alpha \bigtriangledown g + \beta \bigtriangledown h$와 g(x,y) = c, h(x,y) = d의 연립방정식의 해를 구하는 문제가 된다.
혹은 다음과 같이 g(x,y) = c이므로 g(x,y) - c = 0으로 쓸 수 있고 그러면 g(x,y) = c의 제약조건하에서 f(x,y)를 최적화시키는 문제는

위의 함수 L을 최적화하는 문제이다.
이를 x,y,$\lambda$로 각각 편미분하여 최적화시킬 수 있다.
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| batch normalization 개념 간단하게 (0) | 2024.04.15 |
|---|---|
| hyperparameter 개념 간단하게 (0) | 2024.04.02 |
| gradient descent를 위한 gradient vector의 이론적 설명 간단하게 (0) | 2024.03.01 |
| reproducibility를 위한 random seed (0) | 2023.12.11 |
| 구현하면서 배우는 weight initialization(가중치 초기화) 중요성 (0) | 2023.09.13 |

