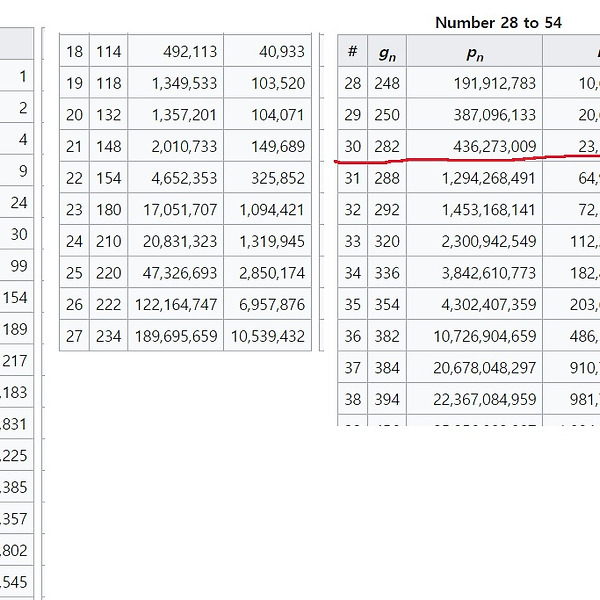
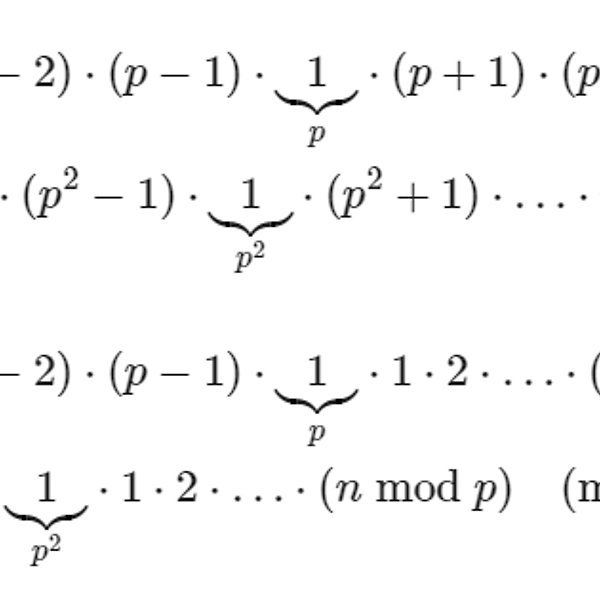연분수(continued fraction)를 이용한 선형 디오판토스 방정식의 해를 구하는 방법
1. 연분수 표현에서 a,b의 최대공약수를 바로 구하는 방법 $\frac{A}{B}$의 연분수 표현을 구하고자 한다면, A/B가 기약분수 형태로 들어가줘야한다. 기약분수로 바꿀려면 A,B의 최대공약수가 g = gcd(A,B)일때, $p_{k} = A/g, q_{k} = B/g$이고 그래서 $\frac{A}{B} = \frac{p_{k}}{q_{k}}$이다. 따라서, A/B가 기약분수가 아닐때, 연분수 표현 p,q를 구한 다음 A를 p[-1]로 나눠주면 A,B의 최대공약수가 된다. #A/B가 기약분수가 아닐때, A,B의 최대공약수 구하기 def continued_fraction(p,q): f = [] while q != 0: f.append(p//q) p,q = q,p%q return f def conve..