Factorial modulo p - Algorithms for Competitive Programming (cp-algorithms.com)
Factorial modulo p - Algorithms for Competitive Programming
Factorial modulo $p$ In some cases it is necessary to consider complex formulas modulo some prime $p$, containing factorials in both numerator and denominator, like such that you encounter in the formula for Binomial coefficients. We consider the case when
cp-algorithms.com
5. 팩토리얼과 이항계수 :: rkm0959 (tistory.com)
5. 팩토리얼과 이항계수
관련 코드는 github에서 찾아볼 수 있다. 이 글에서는 팩토리얼과 이항계수를 $n$으로 나눈 나머지를 계산하는 방법에 대하여 다룬다.중국인의 나머지 정리를 기반으로 한 아이디어는 여기서도 등
rkm0959.tistory.com
n!에서 modulo p를 모두 제거한 경우를 생각한다.
예를 들어 7! mod 3을 구하고 싶다면.. $7! = 1*2*3*4*5*6*7$에서 3을 모두 제거하면..
$7!_{3} = 1*2*1*4*5*2*7$이다.
일반적인 경우로 생각하면 다음과 같이 나타난다
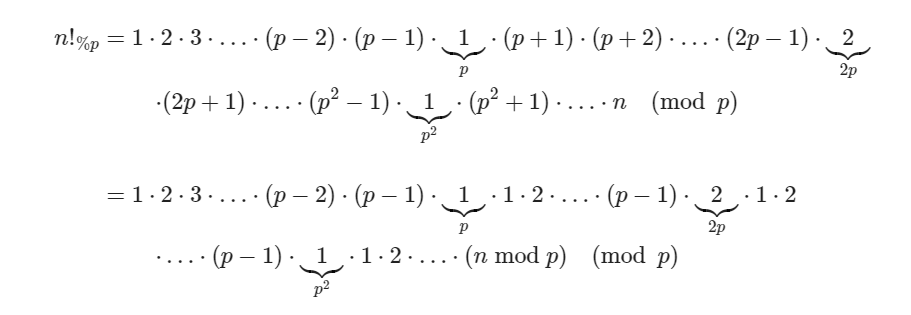
즉 n!에서 p를 모두 제거하면 (p-1)!이 반복되어져서 곱해지다가, 마지막에 (n mod p)!이 곱해지는 형태로 나타낼 수 있다.
(p-1)!이 몇개 나오나? n//p개만큼 나온다.
그러므로, $$n!_{p} = ((p-1)! mod p)^{n//p} * (n mod p)!$$
--------------------------------------------------------------------------------------------------------------------------
(p-1)! mod p를 계산하는데 유용한 정리가 wilson's theorem이다.
"2 이상의 자연수 p에 대하여 p가 소수일 필요충분조건은 (p-1)! ≡ -1 (mod p)"
--------------------------------------------------------------------------------------------------------------------------
그러므로, modulo p가 소수이면..
$$n!_{p} = (-1)^{n//p} * (n mod p)!$$
이제 n!에 e개의 p를 제거했다고 하자. 즉, n!이 원래 e개의 p를 인수로 가진다.
예를 들어 7!은 2개의 3을 인수로 가져서 e = 2이다.
--------------------------------------------------------------------------------------------------------------------------
e는 어떻게 구하는지, 이미 배웠다
$$\sum_{k = 1} \left \lfloor \frac{n}{p^{k}} \right \rfloor$$
https://deepdata.tistory.com/908
팩토리얼을 계산하지 않고도 소인수분해하는 기본기
1. 문제 15996번: 팩토리얼 나누기 (acmicpc.net) 15996번: 팩토리얼 나누기 음이 아닌 정수 N와 소수(prime number) A가 주어지면, N!을 Ak로 나누었을 때, 나머지가 0이 되는 최대의 음이 아닌 정수 k를 구하여
deepdata.tistory.com
Legendre's formula이라고 이름이 붙어있다
$p^{e}$가 n!을 나누어 떨어지게 하는 가장 큰 e를 찾는 공식
Legendre's formula - Wikipedia
Legendre's formula - Wikipedia
From Wikipedia, the free encyclopedia In mathematics, Legendre's formula gives an expression for the exponent of the largest power of a prime p that divides the factorial n!. It is named after Adrien-Marie Legendre. It is also sometimes known as de Polign
en.wikipedia.org
--------------------------------------------------------------------------------------------------------------------------
그러면 $$n! = n!_{p} * p^{e}$$
그러므로, 합동식의 성질을 이용하면 n! mod p는 다음과 같다.
$$n! ≡ (n!_{p} mod p) * (p^{e} mod p) ≡ -1^{n//p} * (n mod p)! * (p^{e} mod p)$$
식을 잘 보면 n! 대신에 (n mod p)!을 구하면 된다는 사실을 알 수 있다
n mod p는 0,1,2,3,4,... p-1까지이므로 p가 n에 비해 충분히 작다면 n!을 아주 빠르고 효율적으로 계산할 수 있게 해준다
n,p = map(int,input().split())
result = (-1)**(n//p)
for i in range(1,n%p+1):
result *= i
result %= p
count = 0
x = p
while n//x > 0:
count += n//x
x *= p
print(result * pow(p,count,p) % p)'정수론' 카테고리의 다른 글
| 연속하는 두 소수 차이는 생각보다 크지 않다(prime gap) (0) | 2023.08.13 |
|---|---|
| n과 소수 p가 매우 클 때 wilson's theorem와 fermat's little theorem을 이용한 n! mod p 구하기 (0) | 2023.08.05 |
| 3개 이상의 연속된 자연수의 합은 반드시 소수가 아니다 (0) | 2023.08.02 |
| 10진법 정수를 등비수열 합으로 바라보기(Fermat number?) (0) | 2023.07.15 |
| 디오판토스 분수방정식의 정수 해법 배우기(+팩토리얼 인수분해, 제곱수의 약수의 개수) (0) | 2023.07.14 |

