https://cp-algorithms.com/string/prefix-function.html
Prefix function - Knuth-Morris-Pratt - Algorithms for Competitive Programming
Prefix function. Knuth–Morris–Pratt algorithm Prefix function definition You are given a string $s$ of length $n$. The prefix function for this string is defined as an array $\pi$ of length $n$, where $\pi[i]$ is the length of the longest proper prefix
cp-algorithms.com
1. prefix function
길이 n인 문자열 s가 있다.
이 때, 길이 n인 배열 $\pi$에 대하여 부분 문자열 s[0,1,...,i]의 proper prefix이면서 suffix가 되는 문자열의 가장 긴 길이를 $\pi[i]$라고 정의하자.
문자열의 proper prefix는 문자열의 prefix이지만, 그 문자열 자체는 아니어야한다.
그러므로 정의에 의하면 i = 0인 경우 s[0]의 prefix중 proper prefix는 존재하지 않으므로, $\pi[0] = 0$
수학적으로 다음과 같이 쓸 수 있다.
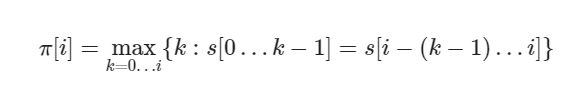
2. 구현 예시
정의 그대로 구현하면 다음과 같이 쓸 수 있다.
def prefix_function(s):
n = len(s)
pi = [0]*n
for i in range(n):
for k in range(i+1):
if s[:k] == s[i-k+1:i+1]:
pi[i] = k
return pi
print(prefix_function("abcabcd"))
print(prefix_function("aabaaab"))
[0, 0, 0, 1, 2, 3, 0]
[0, 1, 0, 1, 2, 2, 3]
"abcabcd"를 보면 정의로부터 $\pi[0] = 0$이고,
i = 1인 경우, s[0,1] = "ab"인데 proper prefix인 경우는 "a" 하나 있고, suffix는 "b" 하나 있는데 둘이 다르니 $\pi[1] = 0$
i = 2인 경우, s[0,2] = "abc"인데 proper prefix인 경우는 "a", "ab"가 있고 suffix는 "c", "bc"가 있는데 서로 다르니 $\pi[2] = 0$
i = 3인 경우, s[0,3] = "abca"인데 proper prefix인 경우는 "a", "ab", "abc"가 있고 suffix는 "a", "ca", "bca"가 있고,
"a"로 서로 같은 경우 있으니 $\pi[3] = 1$
i = 4인 경우 s[0,4] = "abcab"가 있고 proper prefix인 경우는 "a", "ab", "abc", "abca"가 있고
suffix인 경우는 "b", "ab", "cab", "bcab"가 있고 "ab"가 서로 같으면서 가장 기니까 $\pi[4] = 2$
i = 5인 경우 s[0,5] = "abcabc"가 있고 proper prefix인 경우는 "a", "ab", "abc", "abca", "abcab"가 있고
suffix인 경우는 "c", "bc", "abc", "cabc", "bcabc"가 있고 서로 같은 경우는 "abc"가 가장 기니까 $\pi[5] = 3$
i = 6인 경우 s[0,6] = "abcabcd"가 있고 proper prefix인 경우는 "a", "ab", "abc", "abca", "abcab", "abcabc"가 있고
suffix인 경우는 "d", "cd", "bcd", "abcd", "cabcd", "bcabcd"가 있고 놀랍게도 서로 같은 경우는 존재하지 않는다
$\pi[6] = 0$
그래서 $\pi = [0,0,0,1,2,3,0]$
하지만 이 알고리즘은 $O(N^{3})$이라 N이 조금만 커도 느려서 실전성이 부족하다.
3. 첫번째 최적화
첫번째로 관찰할 수 있는 점은 prefix function이 최대 1만큼 증가할 수 있다는 점이다.
만약 $\pi[i+1] > \pi[i] + 1$이면 어떤 상황이 생기는지 생각해보자.
다음 그림은 $\pi[i+1] = 4$이고, $\pi[i] = 2$인 경우이다.

위치 i에서 가장 긴 proper suffix의 길이가 2이고 위치 i+1에서 길이는 4라고 하자.
i+1에서 prefix와 suffix가 서로 같으므로, $s_{0}s_{1}s_{2}s_{3}$은 $s_{i-2}s_{i-1}s_{i}s_{i+1}$과 서로 같다.
그러므로 $s_{0}s_{1}s_{2}$와 $s_{i-2}s_{i-1}s_{i}$가 서로 같으므로 $\pi[i] = 3$이다.
이는 $\pi[i] = 2$가 모순이라는 뜻으로, $\pi[i+1]$과 $\pi[i]$의 차이는 커봐야 1이다.
즉 i가 1 증가할때, prefix function의 값은 1 증가하거나, 그대로이거나, 일부 감소하거나 셋중 하나이다.
이를 이용하면 알고리즘의 시간복잡도를 $O(N^{2})$으로 줄일 수 있다.
왜냐하면, 한 스텝 증가하면, 최대 1만큼 증가할 수 있기 때문이다.
전체적으로 함수는 최대 N 스텝까지 증가할 수 있고, 그러므로 최대 N 스텝까지 감소할 수 있다.
이는 O(N) 문자열 비교 과정만 수행하면 된다는 뜻으로, 시간복잡도는 $O(N^{2})$이다.
pi[0] = 0이니까 i = 1부터 하고, k로 가능한 경우가 0~pi[i-1] + 1까지라는 뜻이니까 이것만 바꿔보면...
def prefix_function(s):
n = len(s)
pi = [0]*n
for i in range(1,n):
for k in range(pi[i-1]+2):
if s[:k] == s[i-k+1:i+1]:
pi[i] = k
return pi
이게 맞는건지 모르겠는데... 첫번째 구현과는 시간차이가 분명히 있음
길이가 5500인 문자열을 이용해서 두 함수 결과와 시간 차이를 비교해봤는데.. 맞게 하긴 한듯..?

4. 두번째 최적화
다음으로 문자열 비교 과정을 제거하고 싶다. 이를 위해 이전에 계산된 모든 정보를 사용할 필요가 있다.
i번째까지 계산하고나서, 다음 i + 1에서 prefix function의 값 $\pi$를 계산하고 싶다.
만약, i+1번째 문자와 $\pi[i]$번째 문자가 서로 같다면 즉 $s[i+1] = s[\pi[i]]$라면.. 우리는 확실하게 $\pi[i+1] = \pi[i] + 1$이라고 할 수 있다.
왜냐하면, 이미 우리는 길이 $\pi[i]$의 i번째 위치의 suffix와 prefix가 동일하다는 것을 알고 있기 때문이다.
다음은 $\pi[i] = 3$인 경우 위 설명에 대한 그림이다.
$s[i+1] = s[\pi[i]] = s[3]$이라면, $s[0,1,2,3] = s[i-2,i-1,i,i+1]$이므로... $\pi[i+1] = \pi[i] + 1 = 4$이다.

하지만, $s[i+1] ≠ s[\pi[i]]$일 수 있다.
그러면 $\pi[i+1]$은 커봐야 $\pi[i]$이므로, i번째 가장 긴 proper prefix보다 더 짧은 문자열에서 suffix와 같은지 찾아봐야한다.
여기서 $j < \pi[i]$인 가장 큰 j를 즉시 찾고 싶다.
즉, s[0,1,...,j-1] = s[i-j+1,...,i]가 되는 가장 큰 j를 빠르게 찾을 수 있을까?

실제로 그러한 길이 $j < \pi[i]$를 찾았다면, 우리는 s[i+1]과 s[j]만 비교하면 된다.
만약 다음과 같이 s[i+1] = s[j]라면 $\pi[i+1] = j + 1$이다.
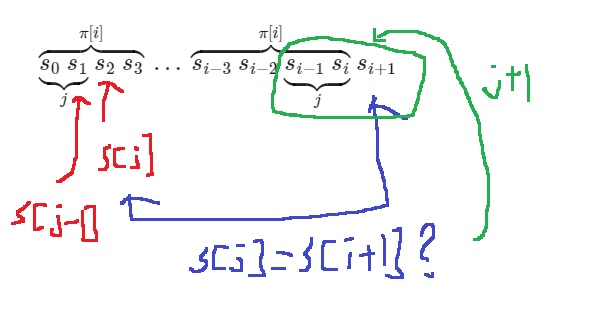
하지만 s[i+1] ≠ s[j]라면, j보다 작으면서 가장 큰 값을 찾을 필요가 있다.
이를 j = 0까지 반복해서 수행하면 된다.
만약 s[i+1] = s[0]라면 $\pi[i+1] = 1$이고 그렇지 않다면 $\pi[i+1] = 0$이다.
우리는 이 알고리즘의 전체적인 흐름을 파악했다.
마지막으로 남은 의문은 j를 어떻게 하면 효율적으로 찾을 수 있는가?이다.
다시 한번 생각해보면 i번째 위치에 대하여, 현재 j는 s[0,1,...,j-1] = s[i-j+1,...,i]를 만족해야한다.
그리고 우리는 다음 성질을 만족하는 가장 큰 k < j를 찾아야한다.

위 그림에서 볼 수 있듯이, 그러한 k는 $\pi[j-1]$이 될 수 있고, 이는 이미 계산해놓은 값이다.
5. KMP 알고리즘
그러면 우리는 어떠한 문자열 비교를 수행하지 않고 prefix function을 O(N)에 구현할 수 있다.
1) i = 0일때, $\pi[0] = 0$이고, i = 1부터 n-1까지 $\pi[i]$를 계산한다.
2) 현재 $\pi[i]$를 계산하기 위해 변수 j를 i - 1에 대한 가장 긴 suffix의 길이로 설정한다. 즉, $j = \pi[i-1]$이다.
3) s[j]와 s[i]를 비교해서 j + 1 길이의 suffix가 prefix가 된다면, $\pi[i] = j+1$이다.
그렇지 않다면, j를 $\pi[j-1]$로 감소시키고 이를 반복한다.
4) j = 0일때까지 반복하는데 j = 0에서도 여전히 s[j] = s[i]인 경우가 없다면 $\pi[i] = 0$이고, i+1로 이동한다.
다음은 이러한 알고리즘을 구현한 것이다.
def prefix_function(s):
n = len(s)
pi = [0]*n #pi[0] = 0으로 초기화
for i in range(1,n): #i를 1부터 n-1까지 반복
j = pi[i-1] #j = pi[i-1]로 초기화
while j > 0 and s[i] != s[j]: #j > 0일때까지 반복하는데..
j = pi[j-1] #s[i] != s[j]이면, j를 pi[j-1]로 감소시키고..
#반복문을 탈출했는데.. s[i] = s[j]이면 j = j + 1로 만든다음,
#j != 0인데, s[i] = s[j]이면 j+1이 될거고
#j = 0인데 s[i] = s[j]이면 1이 될거고
if s[i] == s[j]:
j += 1
#만들어진 j를 pi[i] = j에 대입
#j = 0인데 s[i] = s[j]이면 위에서 1이 되어 여기서 1이 들어갈거고,
#j = 0인데 s[i] != s[j]이면, 결국에 0이 들어가고
#j != 0이고 s[i] = s[j]이면 j+1이 들어간다.
#j ! = 0인데, s[i] != s[j]이면 위에 while 반복문에서 탈출을 못함
pi[i] = j
return pi
print(prefix_function("abcabcd"))
print(prefix_function("aabaaab"))
[0, 0, 0, 1, 2, 3, 0]
[0, 1, 0, 1, 2, 2, 3]
실제 결과도 같고... 3가지 경우 길이 10000인 문자열에 대해 모두 시간도 비교해보면

6. 응용 - 부분 문자열 찾기
prefix function의 가장 고전적인 응용은 주어진 문자열의 부분 문자열을 찾는 것이다.
찾고자 하는 길이 n인 문자열 s와 길이 m인 텍스트 t가 있을때, t에 s가 존재하는지 아닌지를 알아낼 수 있을까?
1) 새로운 문자열 k = s + # + t를 생성한다.
여기서 #은 s인지 t인지를 구별해주는 구분자이다.
2) k에서 prefix function을 계산한다.
이 0~n+1개를 제외한 prefix function의 의미를 생각해보자. (즉, t에 해당하는 prefix function값이다.)
$\pi[i]$의 정의는 위치 i에서 끝나는, prefix와 일치하는 가장 긴 suffix의 길이를 나타낸다.
만약, i > n에서 $\pi[i] = n$인 그러한 위치 i가 존재한다면... suffix에도 길이 n인 prefix와 완전히 동일한 경우가 k = s + # + t에서 존재한다는 뜻이다.
여기서 길이 n인 prefix는 s이고, suffix쪽은 t에 있으므로, s가 t에 존재한다는 뜻이 된다.

따라서 처음에 s + # 문자열까지 저장하고, 이로부터 prefix function을 모두 계산해놓는다.
그리고 문자열 t를 처음부터 하나씩 읽기 시작해서, prefix function을 구하고
어느 순간 $\pi[i] = n$이 되는 i가 존재한다면... t에 s가 존재한다는 뜻이다.
이를 이용하면 O(N+M)에 이 문제를 해결할 수 있다.
7. 연습문제
1786번: 찾기
첫째 줄에, T 중간에 P가 몇 번 나타나는지를 나타내는 음이 아닌 정수를 출력한다. 둘째 줄에는 P가 나타나는 위치를 차례대로 공백으로 구분해 출력한다. 예컨대, T의 i~i+m-1번 문자와 P의 1~m
www.acmicpc.net
8. 풀이
위 O(N) prefix function을 구현해서 p + # + t에 대한 string으로부터 pi배열을 구하면 되겠다
t가 p에 있느냐 없느냐가 중요한게 아니라 몇번이나 나타나는지를 묻고 있기 때문에,
처음부터 p + # + t를 넣어서 전체 pi 배열을 구하는게 낫겠다
마지막에 t에 p가 있는지 없는지 검사할때 인덱스를 조심해야하는데
pi[i] = n이라는 점은 아래 그림에서도 보이듯이 t[i-n+1,...,i]가 s와 같다는 뜻으로, i - n + 1 위치에 처음으로 p가 나타난다는 뜻이다.

또한, 위 과정에 의하면 t가 시작하는 위치는 n+1부터인데 p가 등장할 수 있는 위치 i는 다음과 같이 2n부터이다.
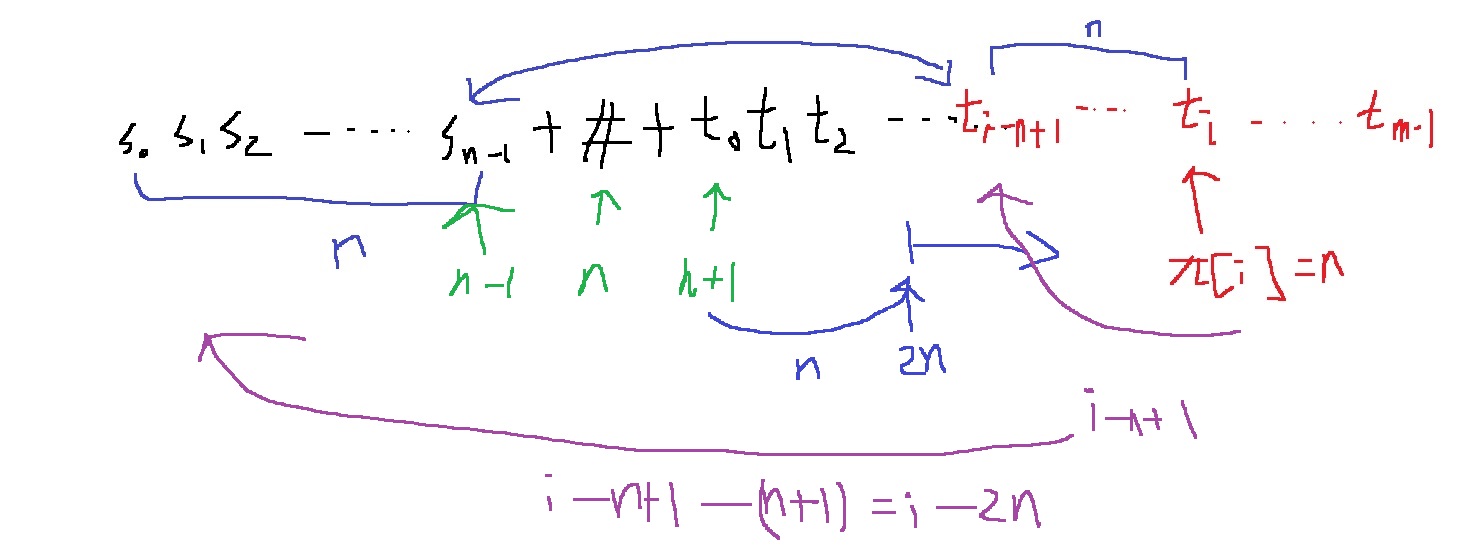
그래서 인덱스 i를 2n부터 m+n+1까지 순회하고 어느 지점 pi[i] = n인 그러한 i가 존재한다면?
i - n + 1에 p가 등장하는 위치라는 뜻인데, 현재 i는 p+#+t라는 새로운 문자열에 대한 인덱스이고..
t의 인덱스만 생각해야한다면 n+1만큼 이동해야하므로 i - n + 1 - (n+1) = i - 2n부터 나타난다는 뜻이다.
그런데 문제에서 1번부터 시작하라고 한다면.. i - 2n + 1에 시작한다고 해야겠지?
#t에 부분문자열 p가 몇번이나 존재하는가?
#KMP prefix function
def prefix_function(s):
n = len(s)
pi = [0]*n
for i in range(1,n):
j = pi[i-1]
while j > 0 and s[i] != s[j]:
j = pi[j-1]
if s[i] == s[j]:
j += 1
pi[i] = j
return pi
t = input()
p = input()
#p#t에 대한 pi배열 구하기
pi = prefix_function(p + "#" + t)
n = len(p)
m = len(t)
count = 0
pos = []
#0~m+n이 p#t의 인덱스이고
#t의 시작 위치는 n+1부터이다.
#그러나 p는 2n부터 등장할 수 있다.
#만약 pi[i] = n인 i가 있다면, p의 등장 위치는 i - n + 1이고
#i는 p#t의 인덱스이므로, n+1만큼 이동시켜서 i - n+1 -(n+1) = i-2n부터 등장한다고 해야한다.
#문제에서 1번부터 시작하라고 한다면 i-2n+1이라고 해야
for i in range(2*n, m + n + 1):
if pi[i] == n:
count += 1
pos.append(i - n + 1 - n)
print(count)
print(*pos)'알고리즘 > 문자열 알고리즘' 카테고리의 다른 글
| 문자열 핵심 자료구조 suffix array O(NlogN) 최적화 배우기 (0) | 2023.08.17 |
|---|---|
| 문자열 핵심 자료구조 suffix array와 lcp(longest common prefix)배열 구하는법 배우기(Manber-Myers, kasai) (0) | 2023.08.16 |
| 문자열 해싱(hashing) 기본 개념 배우기 (0) | 2023.08.08 |
| manacher 응용문제로 이해력 높이기 - 회문인 부분문자열의 개수를 찾는법 (0) | 2023.05.04 |
| manacher algorithm 기본 개념 익혀보기1 (0) | 2023.05.01 |

