1. 문자열의 부분 문자열 중 가장 긴 palindrome의 길이 찾기
abaccaba와 같이 뒤집었을 때 결과가 동일하다면, 그러한 문자열을 palindrome이라고 부른다.
문자열이 하나 주어졌을때, 해당 문자열의 부분 문자열 중 가장 긴 palindrome의 길이를 구하고자 한다.
예를 들어 bananac의 부분 문자열 중 가장 긴 palindrome은 anana로 길이가 5이다.
1-1) 완전탐색($O(N^{3})$)
이 문제를 가장 쉽게 해결하는 방법은 문자열을 순회하면서 가능한 모든 경우에 대해 완전탐색을 수행하는 것이다.
문자열을 앞에서부터 순회하면서, 시작점 후보를 정하고,
나머지 모든 문자 각각을 끝 점 후보로 설정할 때, 좌우대칭인지 여부를 판별해서 길이가 가장 긴 후보를 구하는 방법
input_str = "bananac"
ans = 0
#주어진 문자열이 palindrome인지 판별
def is_palindrome(string):
#하나라도 일치하지 않으면 palindrome이 아니다.
n = len(string)
for i in range(n):
if string[i] != string[n-i-1]:
return False
return True
#문자열을 앞에서부터 순회해서, 시작점 후보를 정한다
for start in range(len(input_str)):
#시작점을 포함한 나머지 문자열을 순회해서, 끝점 후보를 정한다
for end in range(start,len(input_str)):
candidate = input_str[start:end+1]
#문자열이 좌우로 대칭이고 지금까지 저장된 정답보다 긴 경우 답을 갱신한다
if is_palindrome(candidate):
ans = max(ans,len(candidate))
print(ans)
5
이 방법의 시간복잡도는 보면 $O(N^{3})$이다
N이 조금만 크면 매우 느리다
1-2) 최적화1($O(N^{2})$)
관점을 바꿔서 각 문자에 대해 좌우대칭인 문자열의 중심일때를 가정해서, 확장해나가는 완전탐색을 수행할 수 있다.
문자열을 앞에서부터 순회해서 각 문자를 중심점이라 가정하고, 최대 확장 가능한 좌우대칭 문자열을 구하는 것이다.
이 때, 좌우대칭인 문자열은 "aba"와 같은 홀수이거나 "abba"와 같이 짝수일 수 있다.
각각의 경우에 대해 모두 구해준 뒤 최대인 문자열을 구해준다.
이렇게 중심점을 가정한다면, palindrome의 특성상 최대 확장 가능한 좌우대칭 문자열을 O(N)에 찾을 수 있다.
따라서, 중심점 설정에 O(N)에 확장 가능한 범위를 탐색하는데 O(N)의 시간이 소요되어 시간복잡도가 $O(N^{2})$이다.
input_str = "bananac"
ans = 0
def get_max_palindrome_length(start,end):
#문자열의 범위를 벗어나지 않으면서 좌우가 대칭인 경우 확장해나간다
while start >= 0 and end < len(input_str) and input_str[start] == input_str[end]:
start -= 1
end += 1
#while문이 끝났을 때, start와 end는 각각 좌우가 대칭이 깨진 첫 문자의 인덱스를 가리키고 있습니다
start += 1
end -= 1
return end - start + 1
#문자열을 앞에서부터 순회해서 중간점 후보를 정한다
for center in range(len(input_str)):
#최장 palindrome의 길이를 구해 답을 갱신해준다.
ans = max(ans, get_max_palindrome_length(center,center))
# # 문자열을 앞에서부터 순회하며 중간점 후보를 정합니다 (중심 길이는 1).
# for center in range(len(input_str) - 1):
# # 최장 팰린드롬의 길이를 구해 답을 갱신합니다.
# ans = max(ans, get_max_palindrome_length(center, center + 1))
print(ans)
여기서 홀수 길이의 palindrome, 짝수 길이의 palindrome을 구분하지 않고도 코드를 작성하는 방법은..
주어진 문자열 내에 문자 사이사이에 # 문자를 추가해주고, 양쪽 경계 포함해서 가장 긴 홀수 palindrome의 길이를 구해준다.
예를 들어 bananac가 주어진 경우 #b#a#n#a#n#a#n#으로 변경하고 가장 긴 홀수 palindrome을 구한다.
그러면 #a#n#a#n#a#이 된다.
이렇게 #을 추가하게 되면 항상 홀수 길이의 palindrome만 고려해 답을 구하면 되고,
실제 문자열에서 palindrome의 길이는 이렇게 구해진 길이를 2로 나눈 몫이 된다.
여기서 #a#n#a#n#a# 길이는 11이고, 2로 나눈 몫인 5가 정답이다.
----------------------------------------------------------------------------------------------------------
#을 넣어 변형시킬때, join을 이용해야 시간복잡도가 빠르다.
"#"+"#".join(s)+"#"같이
단순히 번갈아 #,문자를 더해나가면, 문자열을 계속 복사하기 때문에 시간복잡도가 매우 상승함
input_str = "bananac"
ans = 0
# 주어진 문자열 내 문자 사이사이에 #을 넣어줍니다. (양쪽 경계 포함)
input_str = "#" + "#".join(input_str) + "#"
def get_max_palindrome_length(start, end):
# 문자열 범위를 벗어나지 않으면서 좌우가 대칭인 경우 확장해나갑니다.
while start >= 0 and end < len(input_str) and \
input_str[start] == input_str[end]:
start -= 1
end += 1
# while문이 끝났을 때 start와 end는 각각 좌우가 대칭이 깨진 첫 문자의 인덱스를
# 가리키고 있기 때문에 이를 보정해줍니다.
start += 1
end -= 1
return end - start + 1
# 문자열을 앞에서부터 순회하며 중간점 후보를 정합니다 (중심 길이는 1).
for center in range(len(input_str)):
# 최장 팰린드롬의 길이를 구해 답을 갱신합니다.
ans = max(ans, get_max_palindrome_length(center, center))
# 처음 주어진 문자열에서
# #을 제외한 부분의 길이가 실제 답이 되기에
# 2로 나눴을 때의 몫이 답이 됩니다.
print(ans // 2)
2. manacher's algorithm
manacher의 알고리즘을 이용하면 최장 홀수 palindrome의 길이를 O(N)에 구할 수 있다
위에서 일반적으로 최장 palindrome의 길이는 #을 문자 사이사이에 붙여서 홀수 palindrome을 구하는 방법으로 계산할 수 있으므로,
최장 홀수 palindrome의 길이만 빠르게 구할 수 있으면 충분하다.
manacher 알고리즘은 먼저 A 배열을 정의한다.
A[i]는 i를 중심으로 하는 홀수 palindrome중 가장 긴 palindrome의 반지름의 길이이다.
구체적으로 [i-A[i], i+A[i]]가 i를 중심으로 하는 최장 홀수 palindrome이 된다.
예를 들어 bananac로 A 배열을 만든다고 할때,
A[4]는 문자 n을 중심으로 하는 홀수 palindrome중 가장 긴 palindrome은 ana이므로 이의 반지름에 해당하는 1이 된다.

이렇게 배열 A를 모두 구해놓는다면, 주어진 문자열 내 부분 최장 홀수 palindrome의 길이는 2A[i]+1의 최댓값이다.
A를 계산하는 가장 간단한 방법은 위에서 설명한것처럼 중심을 기준으로,
양쪽 경계에 있는 문자가 일치하는 한 최대로 확장하는 것이다.
이 방법은 $O(N^{2})$이다.
input_str = "bananac"
#manacher algorithm
n = len(input_str)
A = [0]*n
for i in range(n):
# 0에서 시작
A[i] = 0
# i를 중심으로 최대로 뻗어나간다.
while i - A[i] - 1 >= 0 and i + A[i] + 1 < n and input_str[i-A[i]-1] == input_str[i+A[i]+1]:
A[i] += 1
#최장 홀수 palindrome의 길이를 계산
ans = 0
for i in range(n):
ans = max(ans,2*A[i]+1)
print(ans)
여기서 시간을 줄이는 방법이 있다.
A 배열을 순서대로 채우는 상황에서... A[0], A[1], ... , A[i-1]까지 구해놓고, 이제 A[i]를 구해야하는 상황에서...
A[0],A[1], ... , A[i-1]중 i+A[i] 값이 가장 컸을 경우 i를 p(0,1,2,3,...,i-1중 하나), 그때의 i+A[i] 값을 r이라고 하자.
그러면 r = p+A[p]이다.
이 때, r이 i보다 크다면...

이제 i를 p에 대칭시킬때, 그것을 ii라고 하자.
그러면 ii = 2p-i이다.
p를 기준으로 A[p]만큼 palindrome이므로...
다음 아래 초록색 영역도 대칭이다.

A[0],A[1], ... , A[i-1]까지 구했으므로, p 이전에 존재하는 A[ii]도 이미 알고 있다.
A[ii] > r-i를 만족하면, i를 중심으로 초록색 영역은 확실히 palindrome이므로
(왜냐하면, [p-A[p], p+A[p]]이내는 palindrome이기 때문이다.)
A[i]를 r - i를 시작으로 확장시키는 식으로 시간을 줄일 수 있다.
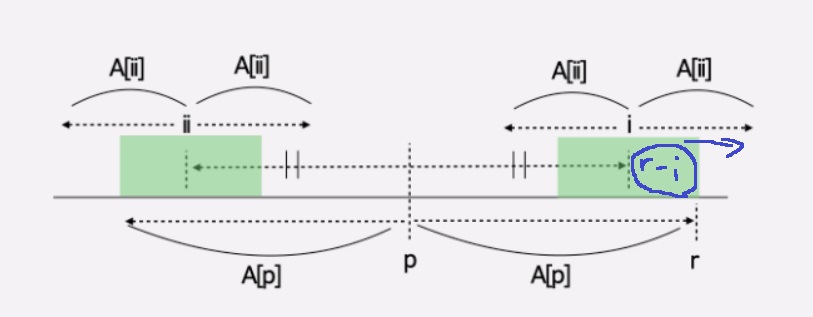
만약 A[ii] <= (r-i)를 만족한다면, i를 중심으로 파란색 영역만큼은 확실히 palindrome임을 알 수 있으므로,
(역시 [p-A[p],p+A[p]] 이내는 확실히 palindrome이기 때문이다)
A[i]를 A[ii]를 시작으로 하여 확장시켜주는 식으로 시간을 줄일 수 있다.
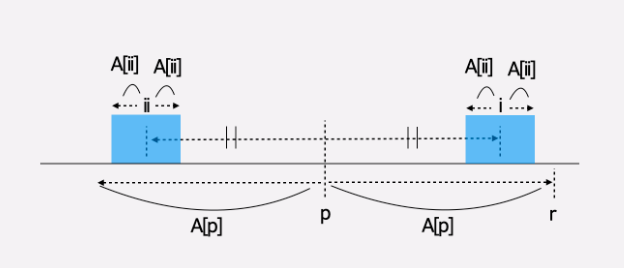
즉 r이 i보다 작다면, 원래대로 A[i]를 0부터 확장하는 것을 진행해야하나,
(왜냐하면, r 이후로는 palindrome인지 알수 없기 때문이다)
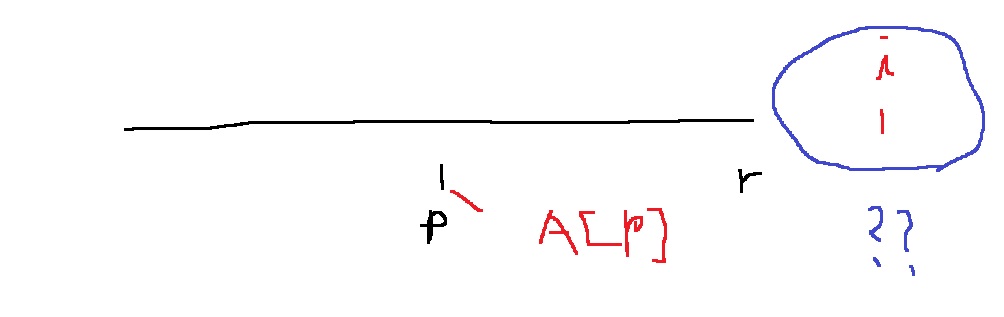
만약 r이 i보다 같거나 큰 상황에 대해서는 A[i]를 min(r-i, A[ii])부터 시작해서 확장하는 식으로 진행이 가능하다.
이러한 방식으로 O(N)에 A의 값을 모두 찾을 수 있다.
상황에 맞는 r,p는 A[i]가 정해지면서 동시에 O(1)에 갱신이 가능하므로 쉽게 계산이 가능하다.
(왜냐하면, r은 지금까지 구한 i+A[i]중 최댓값이고, p는 그 때의 i를 말하기 때문이다)
이렇게 최장 홀수 palindrome을 O(N)에 구할 수 있으므로,
주어진 문자열에 #을 붙여 최장 홀수 palindrome의 길이를 구한 뒤 그 답을 2로 나눈 몫을 구하면 원하는 답을 O(N)에 구할 수 있다.
#주어진 문자열
temp = "bananac"
#주어진 문자열 내 문자 사이사이 #을 넣는다
#join을 이용해 시간복잡도를 줄인다
input_str = "#" + "#".join(temp) + "#"
#manacher algorithm
n = len(input_str) #n은 변형된 문자열의 길이
#A: i번지를 중심으로 하는 홀수 길이의 palindrome중 가장 긴 palindrome의 반지름 길이
#즉, [I-A[i], i+A[i]]가 i를 중심으로 하는 최장 palindrome
A = [0]*n
r = -1
p = -1
#r: j < i를 만족하는 j중 max(j+A[j])
#p: max(j+A[j])가 되는 j의 값
for i in range(n):
#만약 r이 i보다 작다면... 줄일 수 있는 부분이 없어서 A[i] = 0부터
if r < i:
A[i] = 0
#r이 i보다 같거나 크다면, i를 p로부터 대칭시킨 ii에 대하여..
#이미 계산된 A[ii]를 이용해
#i를 중심으로 뻗어나갈 수 있는 적절한 초기값을 O(1)에 설정
else:
ii = 2*p-i
A[i] = min(r - i, A[ii])
#i를 중심으로 최대로 뻗어나간다
while i-A[i]-1 >= 0 and i+A[i]+1 < n and input_str[i-A[i]-1] == input_str[i+A[i]+1]:
A[i] += 1
#i+A[i]중 최대가 되도록, r,p를 갱신
#r은 지금까지 구한 i+A[i]중 최댓값, p는 그 때의 i
if i+A[i] > r:
r,p = i+A[i],i
#최장 palindrome의 길이 계산
answer = 0
for i in range(n):
answer = max(answer,2*A[i]+1)
#처음 주어진 문자열에서 #을 제외한 부분의 길이가 실제 답이 된다.
print(answer//2)
되게 어렵다... 계속 읽어보면서 음미해야할듯;;
3. 연습문제
13275번: 가장 긴 팰린드롬 부분 문자열 (acmicpc.net)
13275번: 가장 긴 팰린드롬 부분 문자열
첫째 줄에 문자열 S가 주어진다. S는 알파벳 소문자로만 이루어져 있으며 길이는 1보다 크거나 같고, 100,000보다 작거나 같다.
www.acmicpc.net
4. 풀이
위에 제시한 알고리즘을 그대로 구현하면 된다.
여기서 주의할점은 #을 붙이는 부분인데..
단순히 번갈아 덧셈으로 구현할 수도 있고
from sys import stdin
s = stdin.readline().rstrip()
shop_s = "#"
for c in s:
shop_s += c
shop_s += "#"
n = len(shop_s)
A = [0]*n
r = -1
p = -1
for i in range(n):
if r < i:
A[i] = 0
else:
ii = 2*p - i
A[i] = min(r-i,A[ii])
while i-A[i]-1 >= 0 and i+A[i]+1 < n and shop_s[i-A[i]-1] == shop_s[i+A[i]+1]:
A[i] += 1
if i+A[i] > r:
r = i+A[i]
p = i
answer = 0
for i in range(n):
answer = max(answer,2*A[i]+1)
print(answer//2)
근데 문자열이 immutable이다 보니 확실히 느리다
join을 이용하면 1/3정도 시간복잡도를 줄일 수 있다
from sys import stdin
s = stdin.readline().rstrip()
#join을 이용해서 시간복잡도를 더욱 줄인다
s = "#"+"#".join(s)+"#"
#n은 변형된 문자열의 길이
n = len(s)
A = [0]*n
r = -1
p = -1
for i in range(n):
if r < i:
A[i] = 0
else:
ii = 2*p - i
A[i] = min(r-i,A[ii])
while i-A[i]-1 >= 0 and i+A[i]+1 < n and s[i-A[i]-1] == s[i+A[i]+1]:
A[i] += 1
if i+A[i] > r:
r = i+A[i]
p = i
answer = 0
for i in range(n):
answer = max(answer,2*A[i]+1)
print(answer//2)
여러 자료들 계속 읽어보면서 연습하는게 답일듯
'알고리즘 > 문자열 알고리즘' 카테고리의 다른 글
| 문자열 해싱(hashing) 기본 개념 배우기 (0) | 2023.08.08 |
|---|---|
| manacher 응용문제로 이해력 높이기 - 회문인 부분문자열의 개수를 찾는법 (0) | 2023.05.04 |
| 컴퓨터로 미분하는 방법(문자열 파싱에서 항상 실수하는 부분 복기) (0) | 2023.04.11 |
| 10진수로 바꾸지 않고 2진수, 8진수 서로 변환하기 (0) | 2023.03.26 |
| 문자열 비교 응용 - 다시 처음부터 되돌아가면서 비교해야할때 (0) | 2023.03.14 |

