String Hashing - Algorithms for Competitive Programming (cp-algorithms.com)
String Hashing - Algorithms for Competitive Programming
String Hashing Hashing algorithms are helpful in solving a lot of problems. We want to solve the problem of comparing strings efficiently. The brute force way of doing so is just to compare the letters of both strings, which has a time complexity of $O(\mi
cp-algorithms.com
1. introduction
길이가 $n_{1}$, $n_{2}$인 2개의 문자열이 있을때, 이 두 문자열을 서로 같은지 다른지 비교하는 방법은?
단순하게 생각하면 문자 하나하나씩 비교해보는 브루트 포스 방법이 있다.
이는 $O(min(n_{1}, n_{2}))$ 시간 복잡도가 걸릴 것이다.
그러므로 두 문자열이 모두 매우 길때, 상당히 오래걸리므로 더 나은 방법을 알고 싶다.
2. string hashing
각각의 문자열을 하나의 정수에 mapping시키고, 문자열 대신에 그 정수들을 비교하는 방법이 있다.
이렇게 하면, $O(min(n_{1}, n_{2}))$ 걸리던 시간이 O(1) 시간으로 단축시킬 수 있다.
문자열을 정수로 변환시키기 위한 hash function이 필요하다.
문자열의 hash라고도 불리는 이는, 문자열을 하나의 정수로 변환시켜준다.
3. hash function
hash function은 다음의 조건을 만족시켜야한다.
" 두 문자열 s,t가 서로 같다면, 그들의 hash값 hash(s)와 hash(t)도 서로 같아야한다. "
여기서 주목할 점은 역이 반드시 성립하지는 않는다는 점이다.
즉, hash(s)와 hash(t)가 서로 같다고 하더라도 반드시 문자열 s와 t가 같다는 보장은 없다.
예를 들어, 각 s에 대해 유효한 hash function이 단순하게 hash(s) = 0이라고 하자.
이 함수는 완전히 무쓸모하지만, 유효한 hash function이다.
무쓸모인 이유는 hash(s) 와 hash(t)가 서로 같다고 하더라도, s와 t가 서로 다른 경우가 지수적으로 많기 때문이다.
15자 보다 짧은 소문자로 구성된 모든 문자열들을 구분해주는 hash function을 원한다고 한다면,
64bit 정수(unsigned long long)로는 만족시킬만한 hash가 존재하지 않는 다는 것을 안다.
왜냐하면 그러한 경우가 너무 많기 때문이다.
물론 우리는 임의의 긴 정수를 비교하길 원하지 않는다. 이 또한 O(n)의 시간복잡도가 소요되기 때문이다.
4. constraint of hash function
그래서 보통 우리는 hash function이 고정된 범위 [0, m)의 정수들을 문자열에 mapping시키길 원한다.
그렇게 한다면 문자열을 비교하는 것은 단순히 고정된 범위의 두 정수를 비교하는 것이다.
물론 이에 더해 hash(s)와 hash(t)가 서로 다르다면, s와 t가 서로 다르길 원한다.
5.hash collision
여기서 중요한 점은 hashing을 사용하는 것이 100% 확실한 방법은 아니라는 점이다.
왜냐하면 완전히 서로 다른 문자열이 동일한 hash를 가질 수 있기 때문이다.
이를 hash collision이라고 부른다.
그러나 많은 경우 서로 다른 두 문자열의 hash가 충돌할 확률이 매우 작아 무시할만하다.
그리고 우리는 그러한 충돌 확률을 낮추기 위한 몇가지 테크닉을 배울 것이다.
6. polynomial rolling hash function
15829번: Hashing
APC에 온 것을 환영한다. 만약 여러분이 학교에서 자료구조를 수강했다면 해시 함수에 대해 배웠을 것이다. 해시 함수란 임의의 길이의 입력을 받아서 고정된 길이의 출력을 내보내는 함수로 정
www.acmicpc.net
hash function은 임의의 길이의 입력을 받아 고정된 길이의 출력을 내놓는 함수이다.
여러 응용분야가 있지만, 대표적으로 자료의 저장과 탐색에 쓰인다.
어떠한 hash function을 생각해볼 수 있을까?
예를 들어 영문 소문자로만 구성된 문자열에 대하여 총 26개의 알파벳이 존재하므로, a에는 1, b에는 2, ... , z에는 26으로 mapping시킨다면...
"abba"라는 문자열은 수열 1,2,2,1로 나타낼 수 있다.
간단하게 이 수열의 값을 모두 더한 하나의 정수를 "abba"의 hash로 정의할 수 있다.
하지만 단순히 더하기만 한다면 정수 값의 범위가 매우 커질 수 있으므로... 수열의 합을 어떤 수 M으로 나눈 나머지로 정의한다면...
$$H = \sum_{i = 0}^{l-1} a_{i} (mod M)$$
그런데 hash function의 입력으로 들어올 수 있는 문자열의 종류는 무한하지만, 출력 범위는 고정되어 있으므로
"비둘기 집의 원리"에 의해 서로 다른 문자열이 동일한 hash 값을 가지는 경우가 반드시 존재하게 된다.
이를 hash collision이라고 부르며 좋은 hash function은 이러한 경우가 최대한 적어야한다.
위 함수는 단순히 문자열의 순서를 바꾼, "abba"와 "baba"가 서로 같은 hash 값을 가질 수 있게 된다.
이를 피하는 한가지 방법으로 수열의 각 항마다 고유한 계수를 부여하는 것이다.
예를 들어, 항의 번호 i에 해당하는 만큼 특정한 숫자 p를 거듭제곱해서 곱해준 다음 더하는 방법이 있다.
길이가 n인 s의 hash를 다음과 같이 정의할때, polynomial rolling hash function이라고 부른다.
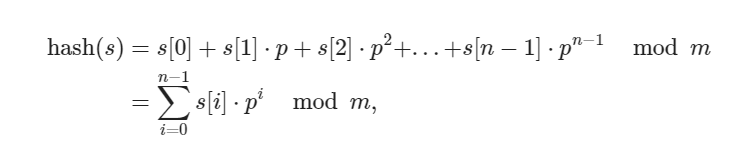
1) 식을 보면 p와 m은 서로소로 정하는 것이 좋다는 것을 알 수 있다.
s[i]*p를 m으로 나눌때, p와 m이 서로소가 아니면 나올 수 있는 나머지 가능성이 줄어들기 때문에 hash 충돌 가능성이 높아진다.
2) p는 input으로 들어오는 문자열이 가질 수 있는 문자의 종류의 개수와 비슷한 소수로 정하는 것이 보통이다.
예를 들어 영어 소문자로만 구성된 문자열이 input으로 들어온다면 p = 31이 좋은 선택이다.
대문자와 소문자를 모두 사용할 수 있다면 p = 53도 가능한 선택이다.
hash(s)가 가질 수 있는 값은 어떤 정수를 m으로 나눈 나머지인 0~m-1 중 하나이므로
두 문자열 s,t가 서로 같은 hash를 가질 확률(충돌 확률)은 대략적으로 $\frac{1}{m}$이다.
이 확률은 m이 클 수록 작아지므로, 최대한 작게 할려면 m은 매우 큰 수를 선택하는 것이 좋다.
모듈로 연산에서 64bit 정수 오버플로우가 일어날 수 있으므로 이를 방지하기 위해 $m = 2^{64}$를 선택하는 경우가 있는데,
여전히 충돌할 수 있는 두 문자열을 선택할 수 있어서 관례적으로 $m = 2^{64}$는 추천하는 선택은 아니다.
3) 그래서 m에 대한 좋은 선택은 매우 큰 소수이다.
$m = 10^{9} + 9$는 충분히 크면서도 64bit 정수를 사용하여 두 값의 곱셈을 수행하기에 작기 때문에 좋은 선택이다.
또한 이 문제에서 m = 1234567891이라는 소수를 선택했다.
n = int(input())
s = input()
s2n = {'a':1,'b':2,'c':3,'d':4,'e':5,'f':6,'g':7,'h':8,
'i':9,'j':10,'k':11,'l':12,'m':13,'n':14,'o':15,
'p':16,'q':17,'r':18,'s':19,'t':20,'u':21,'v':22,'w':23,
'x':24,'y':25,'z':26}
nums = [s2n[c] for c in s]
r = 31
m = 1234567891
answer = 0
for i in range(n):
answer += (nums[i])*pow(r,i,m)
answer %= m
print(answer)
근데 dict를 하나하나 다 쓰기 귀찮다면, ord()함수가 유니코드로 대응시키는 함수라서
'a'를 1에 대응시킨다면, ord(s[i]) - ord('a') + 1을 하면, a,b,c,...,z를 1,2,..,26에 대응시킬 수 있다.
#polynomial rolling hash function
n = int(input())
s = input()
r = 31
m = 1234567891
answer = 0
for i in range(n):
answer += (ord(s[i]) - ord('a') + 1)*pow(r,i,m)
answer %= m
print(answer)'알고리즘 > 문자열 알고리즘' 카테고리의 다른 글
| 문자열 핵심 자료구조 suffix array와 lcp(longest common prefix)배열 구하는법 배우기(Manber-Myers, kasai) (0) | 2023.08.16 |
|---|---|
| KMP(Knuth–Morris–Pratt) 알고리즘 배우고 부분문자열 검색하는 방법 익히기 (0) | 2023.08.10 |
| manacher 응용문제로 이해력 높이기 - 회문인 부분문자열의 개수를 찾는법 (0) | 2023.05.04 |
| manacher algorithm 기본 개념 익혀보기1 (0) | 2023.05.01 |
| 컴퓨터로 미분하는 방법(문자열 파싱에서 항상 실수하는 부분 복기) (0) | 2023.04.11 |

