1. 가중치에 음수가 포함된 경우
모든 간선의 비용이 양수일때는 다익스트라 알고리즘을 사용하면 특정 노드에서 다른 노드까지 최단 거리로 가는 비용을 효과적으로 구해준다
다음에서 1번 노드에서 다른 노드까지 가는 최단 비용은 얼마일까?

다익스트라 알고리즘을 이용해서 구하면 최단거리를 간단히 구할 수 있다
import heapq
INF = 10000000000000000000000
dist = [INF]*7
graph = [[],[(2,6),(3,2)],[(3,2),(4,2)],[(5,1)],[(6,2)],[(2,1),(4,3),(6,4)],[]]
q = []
heapq.heappush(q,(0,1))
dist[1] = 0
while q:
d,u = heapq.heappop(q)
if dist[u] < d:
continue
for v,c in graph[u]:
cost = dist[u] + c
if dist[v] > cost:
dist[v] = cost
heapq.heappush(q,(cost,v))
print(dist[1:])
[0, 4, 2, 6, 3, 7]
1번 노드부터 각 노드까지 거리가 0,4,2,6,3,7의 최단거리로 도달할 수 있다는 뜻
그런데 만약 그래프가 다음과 같다면?
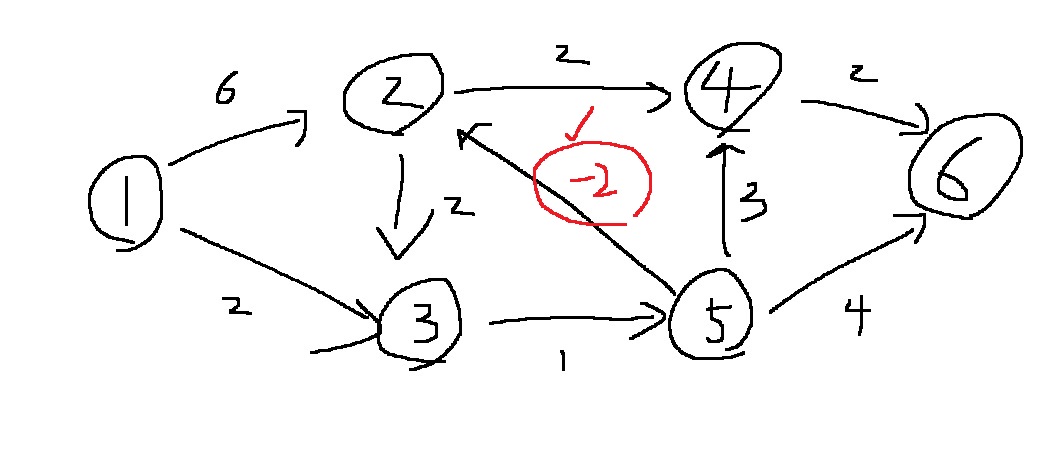
5번 노드에서 2번 노드로 가는 간선의 가중치가 -2로 바뀐다면?
여전히 최단거리를 계산할 수는 있을 것이다
대충 눈으로만 보더라도
1번에서 3번까지는 2의 비용으로
1번에서 5번까지는 2+1의 비용으로
1번에서 2번까지는? 1>3>5>2로 가서 1의 비용으로 갈 수 있을 것이다
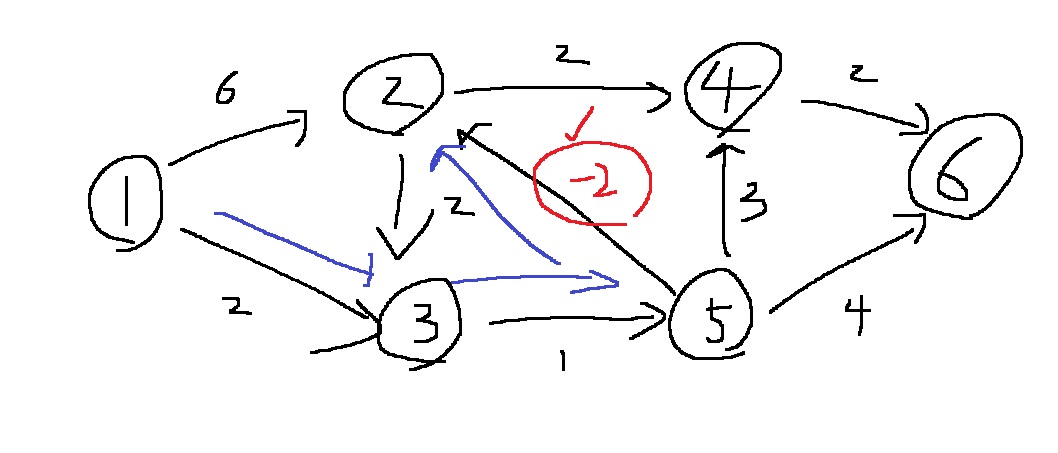
그러면 1번에서 4번까지는? 1번에서 2번까지 1의 비용으로 가고, 4번으로 가면 3의 비용으로
1번에서 6번까지는? 1번에서 4번까지 3의 비용으로 가고, 6번으로 가면 5의 비용으로 갈 수 있을 것이다
[0,1,2,3,3,5]가 될 것인데

(다익스트라도 똑같이 나오긴 하네;;)
아무튼 음수 가중치를 가지는 간선이 있다고 해서 최소 비용을 결정짓지는 못하는 것은 아니다
2. 음수 간선의 순환(negative cycle)이 포함된 경우
하지만 최소 비용을 특정하지 못하는 경우가 존재할 수 있는데

위와 같은 경우 2 > 3 > 5로 이동하는 cycle이 존재하는데, 모든 가중치의 합이 -1이라는 것을 알 수 있다
그렇다면, 1번 노드에서 6번 노드로 가기 위한 최단 비용을 생각해본다면..?
1 > 3 > 5 > 2 > 4 > 6으로 2 + 1 + -4 + 2 + 2 = 3으로 구할 수 있었는데,
만약에 바로 6번으로 가지 않고 2 > 3 > 5를 한번 돌면 비용이 -1이니까, 2 > 3 > 5를 계속 돌수록 비용을 1씩 줄일 수 있으므로
만약에 6번으로 가기전에 2 > 3 > 5를 무한히 돈다면?
그러면 1 > 6으로 가는 비용을 무한히 줄일 수 있다는 뜻이 된다
따라서 음수 간선의 순환이 포함된 그래프에서는 최단 거리 비용이 음의 무한인 노드가 존재할 수 있다
위의 경우는 모든 노드에서 사이클을 무한히 돈다면, 음의 무한으로 줄일 수 있다
3. 최단 경로 문제
최단 경로 문제는 다음과 같이 분류할 수 있을 것이다
3-1) 모든 간선의 가중치가 양수인 경우
3-2) 간선의 가중치에 음수가 있는 경우
>> 3-2-1) 음수 간선의 순환(negative cycle)이 존재하는 경우
>> 3-2-2) 음수 간선의 순환이 존재하지 않는 경우
4. 벨만 포드 알고리즘
벨만 포드 알고리즘은 음수 가중치가 포함된 간선이 존재하는 경우에도 특정 노드에서 출발하여 특정 노드로 도달하는 최단 거리를 구할 수 있게 해준다
또한 음수 간선의 순환(negative cycle)을 감지할 수 있다
위에서 제시한 최단 경로 문제의 모든 경우를 커버할 수 있다
하지만 기본적인 시간 복잡도는 정점의 개수가 V개이고 간선의 개수가 E개 이면 O(VE)로 다익스트라 알고리즘에 비해 느리다
5. 알고리즘 원리
5-1) 출발 노드를 설정한다
5-2) 최단 거리 테이블을 초기화한다
>> 다른 모든 노드에 대해 거리가 무한이라고 초기화
5-3) 다음의 과정을 V-1번 반복한다(V는 정점의 개수)
>> 매번 전체 간선 E개를 모두 확인한다
>> 각 간선을 거쳐서 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다
5-4) negative cycle이 존재하는지 체크하고 싶다면, 5-3)을 한번 더 수행한다
>> 만약 이 경우에도 최단 거리 테이블이 갱신된다면, negative cycle이 존재하는 것이다
6. 벨만 포드 vs. 다익스트라
다익스트라 알고리즘도 v-1번 만큼 반복을 진행하지만, 모든 간선을 체크하지는 않고 특정 노드에 붙어있는 간선만 체크한다
다익스트라 알고리즘은 따라서 벨만 포드보다 더 적은 개수의 간선을 체크한다
그래서 벨만 포드 알고리즘은 다익스트라 알고리즘의 솔루션을 포함한다
그러므로 모든 가중치가 양수더라도 벨만 포드 알고리즘으로 답을 구할 수는 있지만, 간선을 체크하는 경우가 더 많아서 훨씬 느리다(그러니까 가중치에 음수가 없다면 벨만 포드 알고리즘을 쓸 필요는 없다)
6-1) 다익스트라
매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택함
음수 간선이 없다면 최적 해를 찾을 수 있음
음수 간선이 있다면 문제가 있을 수 있음
6-2) 벨만 포드
매번 모든 간선을 전부 확인 >> 따라서 다익스트라 알고리즘의 최적해를 항상 포함
다익스트라 알고리즘에 비해 시간이 오래 걸리지만, 음수 간선의 순환을 탐지할 수 있다
7. 구현 예시
정점의 수 n에 대해 n-1번 반복하여 매 반복마다 모든 간선 m개를 확인하는데...
만약 음수 순환 탐지가 필요하다면.. n번 반복해서, n번째 반복때에도 거리가 갱신된다면 음수 순환이 존재하는 것이다
INF= int(1e9) #무한을 의미하는 값
#벨만 포드 알고리즘
def bf(start):
#시작 노드에 대해 거리를 0으로 초기화
dist[start] = 0
#n-1번의 라운드를 반복한다
#음수 간선의 순환을 탐지하고자 한다면, 1번 더 반복해서 n번을 반복한다
for i in range(n):
#매 라운드마다 존재하는 모든 간선을 확인한다
for j in range(m):
u = edges[j][0]
v = edges[j][1]
cost = edges[j][2]
#시작점에서 현재 간선에 도달할 수 있고(dist[u]가 무한이 아니다)
#도착점의 현재 최단거리가, 시작점을 거쳐서 가는 비용보다 큰 경우에..
if dist[u] != INF and dist[v] > dist[u] + cost:
#최단 거리를 갱신
dist[v] = dist[u] + cost
#n-1번 모두 갱신시키고 나서
#n번째 라운드에서조차도 값이 갱신된다면.. negative cycle이 존재하는 것이다
if i == n-1:
return True
return False #negative cycle이 존재하지 않음
#노드의 개수, 간선의 개수
n,m = map(int,input().split())
#간선에 대한 정보
edges = []
for _ in range(m):
#노드 a에서 노드 b로 가는 비용이 c이다.
a,b,c = map(int,input().split())
edges.append((a,b,c))
#최단 거리 테이블을 모두 무한으로 초기화
dist = [INF] * (n+1)
#벨만 포드 알고리즘을 수행한다
negative_cycle = bf(1) #출발노드는 1이라고 설정
if negative_cycle: #음수 순환이 존재하면..
print(-1)
else: #음수 순환이 존재하지 않는다면..
for i in range(2,n+1): #1번 말고 다른 노드까지 도달 최단 거리
if dist[i] == INF: #최단거리가 갱신되지 않았다면 도달 불가능
print(-1)
else: #최단 거리가 갱신되었다면 도달 가능
print(dist[i])
8. 연습문제
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
위에거 그대로 쓰면 정답
출처
코딩 테스트를 위한 벨만 포드 알고리즘 7분 핵심 요약 - YouTube
'알고리즘 > 최단거리 알고리즘' 카테고리의 다른 글
| 다익스트라 알고리즘 응용 - 다른 정점에서 목적지로 되돌아오는 최단거리 구하는 방법 (0) | 2023.04.16 |
|---|---|
| 다익스트라 알고리즘 응용하기 - 특정 조건에 맞는 길이를 가진 최단 경로를 구하는 방법 (0) | 2023.01.08 |
| 다익스트라 알고리즘에서 실제 최단 경로 구하기 (0) | 2022.10.10 |
| 최단 거리를 구하는 2번째 알고리즘 플로이드 워셜 알고리즘 파헤치기 (0) | 2022.10.09 |
| 2차원 배열에도 사용가능한 다익스트라 알고리즘 (0) | 2022.10.07 |

