1. 개요
다익스트라 알고리즘은 "한 지점에서 다른 특정 지점까지의 최단 경로를 구해야하는 경우"에 사용할 수 있는 최단 경로 알고리즘이다.
플로이드 워셜 알고리즘은 "모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야하는 경우"에 사용할 수 있는 알고리즘이다.
--------------------------------------------------------------------------------------------------------
다익스트라 알고리즘은 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다.
그리고 해당 노드를 거쳐 가는 경로를 확인하면서 최단 거리 테이블을 갱신하는 방식으로 동작한다.
플로이드 워셜 알고리즘은 또한 단계마다 "거쳐 가는 노드"를 기준으로 알고리즘을 수애한다.
하지만 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다는 점이 다르다.
노드의 개수가 n개일 때 알고리즘 상으로 n번의 단계를 수행하며, 단계마다 $O(N^{2})$의 연산을 통해 "현재 노드를 거쳐가는" 모든 경로를 고려한다.
따라서 플로이드 워셜 알고리즘의 총 시간 복잡도는 $O(N^{3})$이다..
--------------------------------------------------------------------------------------------------------
다익스트라 알고리즘에서는 출발 노드가 1개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해서 1차원 리스트를 활용했다.
반면에 플로이드 워셜 알고리즘은 다익스트라와는 다르게 2차원 리스트에 최단 거리 정보를 저장한다는 특징이 있다.
모든 노드에 대하여, 다른 모든 노드로 가는 최단 거리 정보를 담아야하기 때문이다.
다시 말해 2차원 리스트를 처리하므로 n번의 단계에서 매번 $O(N^{2})$의 시간이 소요된다.
--------------------------------------------------------------------------------------------------------
또한 다익스트라 알고리즘은 그리디 알고리즘이지만, 플로이드 워셜 알고리즘은 다이나믹 프로그래밍으로 볼 수 있다.
노드의 개수가 n개 일때, n번만큼의 단계를 반복하며 "점화식에 맞게" 2차원 리스트를 갱신하므로 다이나믹 프로그래밍으로 볼 수 있다.
-------------------------------------------------------------------------------------------------------
참고로 다익스트라와는 다르게 음의 가중치에서도 사용할 수 있다
2. 기본 알고리즘 설명
각 단계에서는 해당 노드를 거쳐 가는 경우를 고려한다.
예를 들어 1번 노드에서 확인할 때는 1번 노드를 중간에 거쳐 지나가는 모든 경우를 고려하면 된다.
정확히는 A > 1 > B로 가는 비용을 확인하여, 최단 거리를 갱신한다.
이를테면 현재 최단 거리 테이블에서 A번에서 B번으로 가는 비용이 3으로 기록되어 있다면
A번에서 1번을 거쳐 B번으로 가는 비용이 2라는 것이 밝혀지면..
A번에서 B번으로 가는 비용을 2로 갱신하는 것이다.
따라서 알고리즘에서는 현재 확인하고 있는 노드를 제외하고, N-1개의 노드중 서로 다른 노드 (A,B)쌍을 선택한다.
이후 A > 1 > B로 가는 비용을 확인한 뒤에 최단 거리를 갱신한다.
다시 말해 $_{n-1}P_{2}$개의 쌍을 단계마다 반복해서 확인한다.
이때, $O( _{n-1}P_{2} )$는 $O(N^{2})$ 이라고 볼 수 있으므로, 전체 시간 복잡도는 $O(N^{3})$이라고 할 수 있다.
구체적인 K번 단계에 대한 점화식은 다음과 같다.
$$D_{ab} = min( D_{ab} , D_{ak} + D_{kb} )$$
따라서 전체적으로는 3중 반복문을 이용하여 이 점화식에 따라 최단 거리 테이블을 갱신하면 된다.
위의 점화식이 의미하는 내용을 말로 풀어 설명하자면, "A에서 B로 가는 최소 비용"과 "A에서 K를 거쳐 B로 가는 비용"을 비교하여 더 작은 값으로 갱신하는 것이다.
3. 예시를 통해 이해하는 플로이드 워셜 알고리즘
다음과 같은 그래프에 플로이드 워셜 알고리즘을 적용해보자.
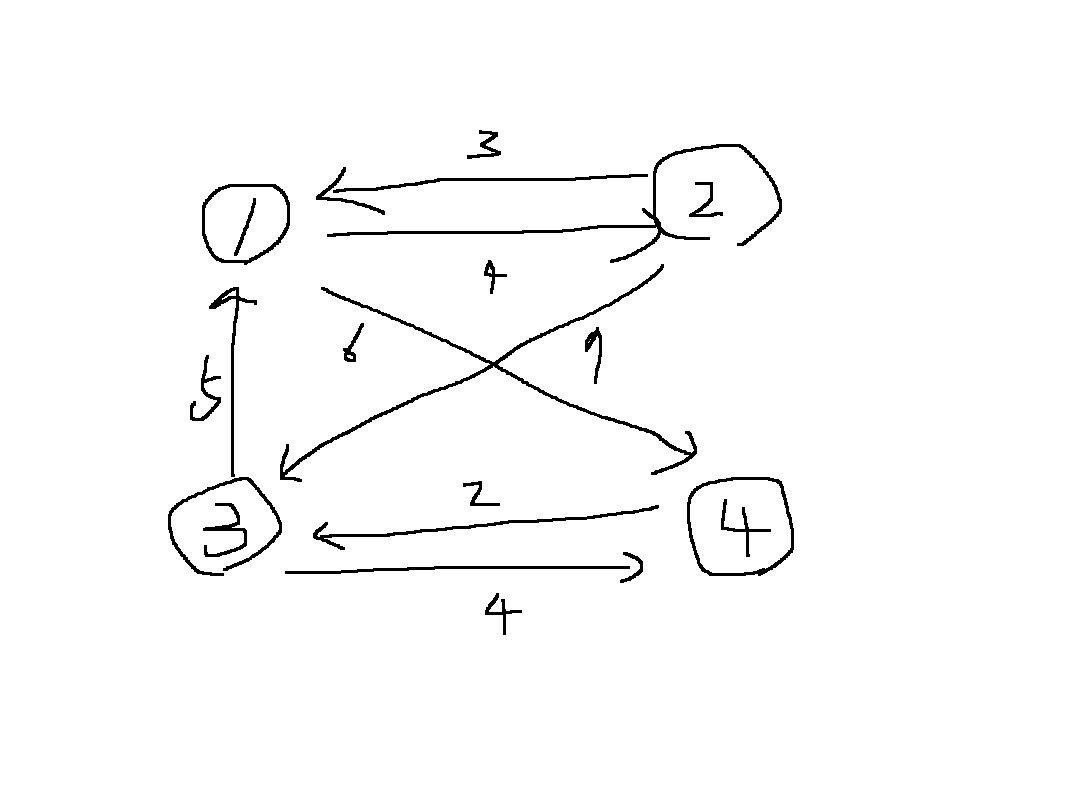
위와 같은 그래프에서 우리는 다음과 같이 초기 테이블을 설정할 수 있다.
연결된 간선은 단순히 그 가중치를 채워넣고, 연결되지 않은 간선은 무한이라는 값을 넣는다.
당연히 실제 구현에서 무한은 10억과 같이 임의의 큰 값을 무한이라고 여기고 넣는다
파이썬에서는 일반적으로 int(1e9)를 이용하는 것이 일반적
표의 각 칸 $D_{ab}$는 a에서 b로 가는 최단거리를 의미한다.
| 출발/도착 | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 4 | 무한 | 6 |
| 2번 | 3 | 0 | 7 | 무한 |
| 3번 | 5 | 무한 | 0 | 4 |
| 4번 | 무한 | 무한 | 2 | 0 |
예를 들어 1번에서 4번으로 가는 비용은 6이므로, 위 표에서 1행 4열의 값은 6이다.
그리고 자기 자신에서 자기 자신으로 가는 비용은 0이므로 모든 1이상 n이하의 모든 i에 대하여 $D_{ii}=0$으로 초기화한다.
즉 왼쪽 위에서 오른쪽 아래로 내려가는 대각선에 놓인 모든 원소는 0이다.
첫번째 단계에서는 단순히 1번 노드를 거쳐서 가는 경우를 고려한다
정확히 다음과 같이 $_{3}P_{2}$가지 경우에 대해 고민하면 된다
그러니까 1번을 제외한 나머지 2,3,4번 노드에서 2가지를 고르는 순열의 수에서 1번을 거쳐가는 비용과 현재 비용을 비교하여 적은 값으로 갱신한다
$$D_{23} = min( D_{23}, D_{21} + D_{13} )$$
$$D_{24} = min( D_{24}, D_{21} + D_{14} )$$
$$D_{32} = min( D_{32}, D_{31} + D_{12} )$$
$$D_{34} = min( D_{34}, D_{31} + D_{14} )$$
$$D_{42} = min( D_{42}, D_{41} + D_{12} )$$
$$D_{43} = min( D_{43}, D_{41} + D_{13} )$$
예를 들어 $D_{23} = min( D_{23} , D_{21} + D_{13} )$은 "기존 2번 노드에서 3번 노드로 가는 비용"보다 "2번 노드에서 1번 노드를 거쳐서 3번 노드로 가는 비용"이 더 작다면, 그것으로 갱신해준다는 의미다.
그래서 $D_{23}$의 값은 $D_{23}$과 $( D_{21} + D_{13} )$중 더 작은 값으로 교체된다.
다시 말해 1을 거쳐 갈 때가 더 빠른 경우가 존재한다면, 빠른 경우로 최단 거리를 갱신해준다는 식이다.
| 출발/도착 | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 4 | 무한 | 6 |
| 2번 | 3 | 0 | 7 | 9 |
| 3번 | 5 | 9 | 0 | 4 |
| 4번 | 무한 | 무한 | 2 | 0 |
위의 표에서 점화식을 계산하고 빈칸을 채워나가면 된다
계산하면 아래와 같다. 예를 들어 $D_{24}$는 원래 무한이였지만, $D_{21}$이 3이고 $D_{14}$가 6이므로 합인 9가 더 작아서 9로 갱신된다
마찬가지로 다음에는 2번 노드를 선택하고, 위와 동일한 과정을 수행한다
2번을 제외한 나머지 1,3,4번 노드에서 2가지를 뽑는 순열의 수는 (1,3), (1,4), (3,1), (3,4), (4,1),(4,3)으로 6가지 경우이다.
각 6가지 경우에 대하여, 예를 들어 (1,3)같은 경우는...
"1번에서 3번으로 가는 비용 무한보다 1번에서 2번으로 거쳐가는 비용 4와 2번에서 3번으로 거쳐가는 비용 7의 합인 11이 더 작다면, 11로 갱신"
| 출발/도착 | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 4 | 11 | 6 |
| 2번 | 3 | 0 | 7 | 9 |
| 3번 | 5 | 9 | 0 | 4 |
| 4번 | 무한 | 무한 | 2 | 0 |
마찬가지로 다음에는 3번 노드를 선택하고 위와 동일한 과정을 반복한다.
3번을 제외한 나머지 1,2,4에서 2가지를 뽑는 순열의 수는 (1,2), (1,4), (2,1), (2,4), (4,1), (4,2)로 6가지이다.
각 6가지 경우에 대하여... 예를 들어 (4,1)의 경우는...
"4번에서 1번으로 가는 비용 무한보다, 4번에서 3번을 거쳐가는 비용 2와 3번에서 1번으로 가는 비용 5의 합인 7이 더 작으므로 7로 갱신"
| 출발/도착 | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 4 | 11 | 6 |
| 2번 | 3 | 0 | 7 | 9 |
| 3번 | 5 | 9 | 0 | 4 |
| 4번 | 7 | 11 | 2 | 0 |
마찬가지로 다음에는 4번 노드를 선택하고, 위의 과정을 반복한다
4번을 제외한 나머지 1,2,3번 노드에 대하여 2가지를 선택하는 순열의 수는 (1,2),(1,3), (2,1),(2,3), (3,1), (3,2)로 6가지이다.
각 6가지 경우에 대하여, 예를 들어 (1,3)의 경우는..
"1번에서 3번으로 가는 비용 11보다, 1번에서 4번을 거쳐가는 비용 6과 4번에서 3번으로 가는 비용 2의 합인 8이 더 작으므로, 8로 갱신"
| 출발/도착 | 1번 | 2번 | 3번 | 4번 |
| 1번 | 0 | 4 | 8 | 6 |
| 2번 | 3 | 0 | 7 | 9 |
| 3번 | 5 | 9 | 0 | 4 |
| 4번 | 7 | 11 | 2 | 0 |
노드의 개수가 4개이므로 4단계의 알고리즘을 수행했다.
그래서 최종적인 테이블은 위와 같고, 여기에 기록된 내용이 "모든 노드에서 다른 모든 노드로 가는 최단 거리 정보"를 표현한다.
예를 들어 $D_{13}$은 8인데, 이는 1번에서 3번으로 가는 최단 거리가 8이라는 뜻이다.
4. 구현 예시
위 알고리즘을 구현하면 다음과 같다. 3중 for문을 수행하므로 시간 복잡도는 노드의 수 n에 대하여 $O(n^{3})$이다.
실제 구현에서는 k를 제외하고 나머지에서 2가지를 뽑는 순열보다.. 그냥 k도 포함시켜서 n개중 2개를 뽑는 순열로 해도 된다
왜냐하면 자기 자신으로 가는 비용은 0이니까
예를 들어 1번을 선택할때, 1,2,3,4중 2개를 뽑는 순열은.. (1,2), (1,3), (1,4),........
그런데 1번에서 2번으로 가는 비용 D[1][2] = min(D[1][2], D[1][1]+D[1][2]) = min(D[1][2],D[1][2]) = D[1][2]로 아무 일도
일어나지 않는다
#플로이드 워셜 알고리즘
INF = int(1e9) ##무한을 의미하는 매우 큰 값
#노드의 개수와 간선의 개수
n = int(input())
e = int(input())
#2차원 인접행렬을 만들고, 모든 값을 무한으로 초기화함
graph = [[INF]*(n+1) for _ in range(n+1)]
#초기 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
#노드는 1번에서 n번까지
for i in range(1,n+1):
graph[i][i] = 0
#각 간선에 대한 정보를 입력받고 그 값으로 인접행렬을 초기화
for _ in range(e):
#a번에서 b번으로 가는 비용은 w
a,b,w = map(int,input().split())
graph[a][b] = w
##점화식 D[a][b] = min(D[a][b], D[a][k]+D[k][b])에 따라 최소 거리를 갱신
##플로이드 워셜 알고리즘 수행
for k in range(1,n+1): ##1번부터 n번까지 노드 선택
for a in range(1,n+1):
for b in range(1,n+1):
graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])
##수행된 결과 출력
for a in range(1,n+1):
for b in range(1,n+1):
##도달할 수 없는 경우는 무한을 출력
##거리가 최초 INF라면, 도달할 수 없는 경우
if graph[a][b] == INF:
print("infinity", end =" ")
else: ##도달 가능한 경우 최단 거리 출력
print(graph[a][b], end = " ")
print()
"""
4
7
1 2 4
1 4 6
2 1 3
2 3 7
3 1 5
3 4 4
4 3 2
0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0
"""
'알고리즘 > 최단거리 알고리즘' 카테고리의 다른 글
| 가중치가 음수인 경우에 최단거리를 구하는 벨만 포드 알고리즘 익히기 (0) | 2022.12.01 |
|---|---|
| 다익스트라 알고리즘에서 실제 최단 경로 구하기 (0) | 2022.10.10 |
| 2차원 배열에도 사용가능한 다익스트라 알고리즘 (0) | 2022.10.07 |
| 특정한 정점을 반드시 거쳐야하는 최단 경로를 구하는 다익스트라 응용 (1) | 2022.10.06 |
| 자다가도 일어나서 바로 구현할 수 있어야하는 최단경로를 찾는 다익스트라 알고리즘 최적화하기 2편 (0) | 2022.10.03 |

