1. 문제
1238번: 파티
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어
www.acmicpc.net
2. 풀이
이 문제의 핵심은 x번 마을에서 다시 i = 1,2,...번 마을로 되돌아오는 최단 거리가 필요하다는 점이다.
다익스트라 알고리즘은
출발 정점 start에서 다른 정점 1,2,...,n번 까지 가는 최단 경로를 구해주는 알고리즘이지
1,2,...,n번 각각의 정점에서 start로 되돌아오는 최단 경로를 구해주는 알고리즘은 아니다
이걸 할려면 다익스트라를 n번 해야하는데 시간제한이 엄격하면 이렇게 풀면 틀릴 가능성이 있다
다익스트라를 1번만 해도 1,2,...,n번 각각의 정점에서 목적지 start로 되돌아오는 최단 경로를 구할 수 있을까
핵심 아이디어는 역방향 그래프를 하나 더 만드는 것이다.
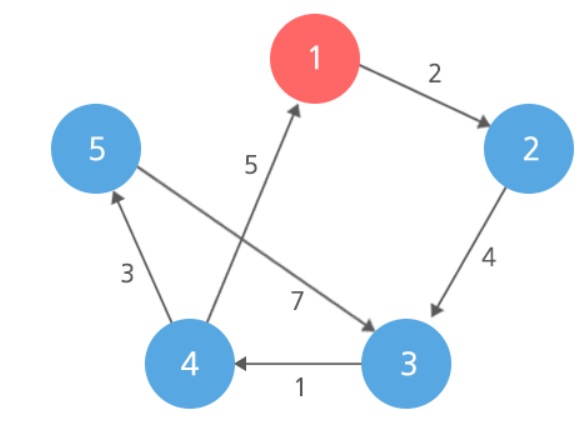
그래프가 위와 같을때, 1번에서 3번으로 가는 최단 경로는 ... 1 > 2 > 4로 2+4 = 6인데...
이 그래프의 간선만 뒤집어서 새로운 그래프를 구성해본다면..? 다음과 같다

이 뒤집은 그래프에서... 1번에서 3번으로 가는 최단 경로를 구해본다면... 1 > 4> 3으로 가는 경로일거고.. 그 거리는 5+1 = 6

그런데, 뒤집은 그래프에서 1 > 4 > 3으로 간다는 것은, 원래 그래프에서 무슨 뜻일까?
다음과 같이, 원래 그래프에서는 3 > 4 > 1로 가는 것과 마찬가지다!

따라서, 뒤집은 그래프에서 1번을 start로 하고, 다익스트라를 수행하면, 1번에서 3번까지 가는 최단 경로는..
1 > 4 > 3으로 6이 될 것인데...
사실 이는 원래 그래프에서 3번에서 1번으로 되돌아오는 최단 경로와 동일하다.
다른 경우도 한번 봐보면 더욱 명백해진다
1번에서 5번으로 가는 경우를 생각해본다면...

원래 그래프에서 1 > 5로 가는 최단 경로는 빨간색 경로일거고...
5 > 1로 되돌아가는 최단 경로는 노란색 경로인데... 이는 뒤집은 그래프에서 1번에서 5번으로 가는 최단 경로인 파란색 경로와 동일하다.
-----------------------------------------------------------------------------------------------------------------------------------
따라서.. 그래프 입력을 받을때, a > b로 가는 cost가 c이면... graph[a].append((b,c))로 입력을 받을건데,
역방향 그래프를 따로 만들어서.. reverse_graph[b].append((a,c))로 구성해준다.
그러면.. graph를 대상으로 x번에서 출발하여 다익스트라를 수행하면.. x번 정점에서 나머지 정점으로 가는 최단 경로를 구해줄거고
reverse_graph를 대상으로 x번에서 출발하여 다익스트라를 수행하면..?
나머지 정점에서 x번 정점으로 되돌아오는 최단 경로를 구해줄것이다.
그러므로.. x번 정점에서 i번 정점으로 왕복하는 최단 경로의 거리는.. 두 다익스트라에서 구한 배열에 대해..
d1[i] + d2[i]로 2번만 다익스트라를 수행하면 구할 수 있게 된다
import heapq
from sys import stdin
def dijkstra(start,graph):
q = []
heapq.heappush(q,(0,start))
INF = 1000000000000000000000
distance = [INF]*(n+1)
distance[start] = 0
while q:
dist,u = heapq.heappop(q)
if distance[u] < dist:
continue
for b,c in graph[u]:
cost = dist+c
if cost < distance[b]:
distance[b] = cost
heapq.heappush(q,(cost,b))
return distance
n,m,x = map(int,stdin.readline().split())
graph = [[] for _ in range(n+1)]
inverse_graph = [[] for _ in range(n+1)]
for _ in range(m):
a,b,c = map(int,stdin.readline().split())
graph[a].append((b,c))
inverse_graph[b].append((a,c))
distance_outcome = dijkstra(x,graph)
distance_income = dijkstra(x,inverse_graph)
ans = 0
for i in range(1,n+1):
cost = distance_income[i] + distance_outcome[i]
if ans < cost:
ans = cost
print(ans)
중요한 아이디어인데 이걸 복기를 안해놨네..
'알고리즘 > 최단거리 알고리즘' 카테고리의 다른 글
| 다익스트라 응용하기 - 시작 정점은 여러개일 수도 있다 (1) | 2023.04.17 |
|---|---|
| 다익스트라 알고리즘 조금 어려운 문제로 오랜만에 재활하기1 (0) | 2023.04.16 |
| 다익스트라 알고리즘 응용하기 - 특정 조건에 맞는 길이를 가진 최단 경로를 구하는 방법 (0) | 2023.01.08 |
| 가중치가 음수인 경우에 최단거리를 구하는 벨만 포드 알고리즘 익히기 (0) | 2022.12.01 |
| 다익스트라 알고리즘에서 실제 최단 경로 구하기 (0) | 2022.10.10 |

