1. 문제
N개의 block이 일렬로 있고 0부터 N-1까지 숫자가 붙어있다.
사이가 안좋은 개구리가 하나의 block위에 함께 있는데 이들이 서로 최대한 멀리 떨어지려고 한다.
만약 J와 K, J<=K의 block위에 각각 개구리가 있다면 그 거리는 K-J+1로 계산한다.
개구리는 오직 현재 위치에서 인접한 block만으로 점프할 수 있고, 현재 위치 block의 높이보다 크거나 같은 block만으로 점프할 수 있다.
두 개구리의 최적의 시작 위치에서 가장 멀리 떨어지게 만들 수 있을까?
N개의 block의 높이가 blocks로 주어지고 이것을 받아 두 개구리의 가장 멀리 떨어진 거리를 return하는 함수를 완성하시오
2. 예시
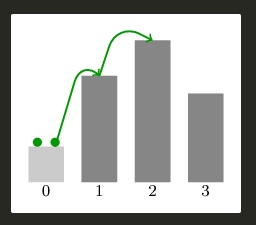
blocks = [2,6,8,5]로 주어지면 최대 거리는 3이다.
그림과 같이 0번 block에서 두 개구리가 시작하고 개구리 한마리가 2번 위치까지 점프를 반복하면 두 개구리의 거리는 3이다.
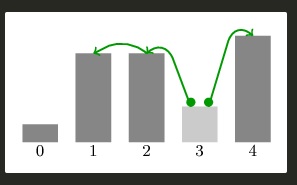
blocks = [1,5,5,2,6]이면 최대 거리는 4이다.
아래 그림처럼 3번 block에서 두 개구리가 시작해서 한마리는 1번까지 반복점프하고 한마리는 4번으로 점프하면 두 개구리의 거리는 4가 된다.
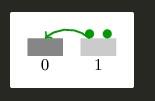
blocks= [1,1]로 주어지면 최대 거리는 2이다.
그림과 같이 1번에서 시작하여 개구리 한마리가 0번으로 점프하면 두 개구리의 거리는 2가 된다.
0번에서 시작해도 마찬가지로 한마리만 1번으로 점프하면 두 개구리의 거리는 2가 된다.
3. 제한사항
N은 2이상 200000이하의 정수
blocks의 각 원소는 1부터 1000000000사이의 정수
4. 풀이
문제의 핵심을 파악할 수 있을까?
두 개구리가 최대가 될려면 어떻게 해야할까?
개구리 한마리는 왼쪽으로 점프해야하고 다른 개구리는 오른쪽으로 점프해야한다
그러면 0번 block부터 N번 block까지 개구리를 세워보고
한마리는 왼쪽으로 최대한 멀리 뛰었을 때 위치를 찾고 다른 개구리는 오른쪽으로 최대한 멀리 뛰었을 때 위치를 찾는다면
그때 거리가 i번 block의 두 개구리의 최대 거리가 된다
i=0부터 N까지 최대 거리를 찾고 이들 중 최대 거리를 찾으면 그것이 답이 될 것
def solution(blocks):
N = len(blocks)
max_distance = 0
for s in range(N):
s_h = blocks[s]
first = s-1
second = s+1그래서 blocks의 길이를 구해서 N으로 저장하고 0부터 N-1까지 돌건에
첫 시작 block의 높이 s_h = blocks[s]이고 오른쪽으로 갈 첫 개구리 first와 왼쪽으로 갈 두번째 개구리 second를 정한다
for ind,h in enumerate(blocks[s::1]):
if h >= s_h:
s_h = h
first += 1
else:
break
현재 s-1에 첫번째 개구리가 시작할건데 blocks의 s부터 오른쪽으로 순회를 해서 h라고 두는거임
만약 h가 시작높이 s_h보다 크거나 같으면 점프할 수 있고 현재 개구리 높이 s_h를 h로 두고 first에 1을 더해서 개구리 위치를 갱신한다
근데 점프를 못하는 순간 더 이상 오른쪽으로는 못간다는 소리이므로 반복문을 탈출
s_h = blocks[s]
#second frog
for ind,h in enumerate(blocks[s::-1]):
if h >= s_h:
s_h = h
second -= 1
else:
break
두번째 개구리의 위치를 찾기 위해 시작 위치의 높이 s_h를 blocks[s]로 초기화시키고
이제 왼쪽으로 순회하기 위해 blocks[s::-1]로 for문을 돈다
첫번째 개구리와 마찬가지로 block의 높이 h가 현재 높이 s_h보다 크거나 같으면 개구리는 점프하고
높이 s_h를 h로 갱신한 다음 왼쪽으로 뛴다니까 현재 위치 second에 -1을 해서 위치도 갱신한다
if first >= second:
distance = first - second + 1
if max_distance <= distance:
max_distance = distance
else:
distance = second - first + 1
if max_distance <= distance:
max_distance = distance
시작 위치 s에서 가장 멀리 뛸 수있는 위치 first와 second를 찾았으므로 그 거리를 구한다.
문제에서 제시한 공식 K>=J이면 K-J+1로 거리를 구한다 했으니까 first >= second이면 first-second+1로 현재 거리를 구하고
최대거리 max_distance와 비교해서 현재 거리 distance가 더 크면 max_distance로 갱신한다
근데 first<=second이면 second-first+1로 거리를 구하겠지만..이라고 생각했는데
아니 first는 오른쪽으로 뛰고 second는 왼쪽으로 뛰어서 무조건 first가 더 크잖아...
다시 보니까 이게 보이네?
def solution(blocks):
N = len(blocks)
max_distance = 0
for s in range(N):
s_h = blocks[s]
first = s-1
second = s+1
#first frog
for ind,h in enumerate(blocks[s::1]):
if h >= s_h:
s_h = h
first += 1
else:
break
s_h = blocks[s]
#second frog
for ind,h in enumerate(blocks[s::-1]):
if h >= s_h:
s_h = h
second -= 1
else:
break
distance = first - second + 1
if max_distance <= distance:
max_distance = distance
return max_distance
최종코드는 위와 같지만 이렇게 하면 N=200000인 최대의 경우에서 시간이 너무 오래걸린다

10분넘게 걸리는건 보통 제한시간이 10초정도인 코딩테스트에서는 바람직하지 못하다
내 생각에 결국 이중 for문이라는게 문제임
0부터 N-1까지 순회하는데 그 안에서 blocks[s::1]이랑 blocks[s::-1] 2개나 더 순회하니까 시간이 오래걸리는 것 같다
최악의 경우 $O(N^{2})$이 걸리나?
------------------------------------------------------------------------------------------------------------------------------
그런데 이게 조금만 더 생각해보면
예를 들어 [1,5,5,2,6]인 경우
0번째에서 개구리가 시작한다고 해보자
0번째에서 오른쪽으로 뛸 수 있는 최대 위치는 2가 된다
그런데 사실 1번째에서 시작한다고 해도 오른쪽으로 뛸 수 있는 최대 위치는 2이다
이것은 0번째에서 시작한 경우는 1번째에서 시작한 경우에 1을 더한 것이라는 사실
그러니까 조금 생각해보면 0번째에서 개구리가 오른쪽으로 뛸 수 있는 최대 위치를 구하는 문제는
1번째에서 개구리가 오른쪽으로 뛸 수 있는 최대 위치를 구한 문제로 이루어져있고
이는 2번째에서 개구리가 오른쪽으로 뛸 수 있는 최대 위치를 구한 문제로 이루어지고...
이런 부분문제들을 풀기만 하면 바로 구할 수 있다는 점을 생각하는 것이 중요하다
--------------------------------------------------------------------------------------------------------------------
이런 원리에 입각해서 문제를 풀어보면
def solution(blocks):
N = len(blocks)
distance = []
first = {}
second = {}
#first frog
for ind in range(0,N):
first[ind] = 0
if ind >0 and (blocks[ind-1] >= blocks[ind]):
first[ind] = first[ind-1] + 1
N은 blocks의 길이로 block의 개수, first, second는 각 개구리가 왼쪽, 오른쪽으로 뛰었을 때 최대 위치를 사전으로 저장할거임
그러면 0부터 N-1까지 오른쪽으로 순회를 해서 개구리의 시작 위치를 ind라고 할거임
만약 [1,5,5,2,6]이라고 가정해보자
시작 개구리는 안뛰었으니까 초기 거리는 0으로 두고
first[0] = 0, first[1] = 0인데, 이제 ind=1은 ind>0잖아
그런데 ind-1 = 0의 높이 blocks[0] = 1는 blocks[1] = 5보다 작기때문에
1번에서 시작하는 개구리는 0번으로 뛸 수가 없다
그래서 0번에서 시작한 개구리는 왼쪽으로 1밖에 못뛰고
1번에서 시작한 개구리는 0번에서 시작한 개구리가 왼쪽으로 뛴 최대거리를 이용해서 구할려고 했는데
1번에서 시작한 개구리가 0번으로 못뛰니까 1번도 마찬가지로 1밖에 못뛴다
first[0] = 0, first[1] = 0, ind=2이면 first[2] = 0인데 ind=2>0이고 blocks[1] = 5, blocks[2] = 5로
--------------------------------------------------------------------------------------------------------------------
2번에서 1번으로는 1칸 점프할 수 있다는 의미
그러면 우리는 2번에서 시작한 개구리가 왼쪽으로 뛸 수 있는 최대 거리는
"(1번에서 시작한 개구리가 왼쪽으로 뛸 수 있는 최대거리) + 1"로 구할 수 있다
그런데 (1번에서 시작한 개구리가 왼쪽으로 뛸 수 있는 최대거리)는 first[1]로 이미 구해서 저장해놨다
내가 처음 푼 풀이는
2번에서 왼쪽으로 뛸 수 있는 최대 거리는 blocks[2::-1]로 0,1,2 모두 검사했지만
이 방법은 blocks[2], blocks[1]만 검사하면 2번에서 왼쪽으로 뛸 수 있는 최대 거리를 바로 구할 수 있다는 점이다
이건 blocks가 길수록 효과가 커진다
100000번에서 왼쪽으로 뛸 수 있는 최대 거리는
99999번으로 못뛴다면 1이지만
99999번으로 뛸 수 있다면
"(99999번에서 왼쪽으로 뛸 수 있는 최대 거리) + 1"으로 구해진다
그런데 내가 처음한 방법은 blocks[100000::-1]로 0,1,2,3,4,5,6,7,....,100000를 모두 검사하는데
이 방법은 blocks[100000], blocks[99999] 2개만 검사하면 답을 낼 수 있다
압도적으로 빨라진다
---------------------------------------------------------------------------------------------------------------------------------------
그래서 [1,5,5,2,6]이면 first[0] = 0, first[1] = 0, first[2] = 1가 되고 ind=3이면 3번에서 2번으로 뛸 수 있으니까
first[3] = first[2] + 1 = 2이 된다, ind=4이면 3번으로는 못뛰니까 first[4] = 0이다
for ind in range(N-1,-1,-1):
second[ind] = 0
if ind < N-1 and (blocks[ind+1] >= blocks[ind]):
second[ind] = second[ind+1] + 1
비슷하게 두번째 개구리도 생각할 수 있다
N-1부터 0까지 왼쪽으로 순회하기 위해 range(N-1,-1,-1)을 사용했다
[1,5,5,2,6]을 생각해보고
먼저 second[4] = 0이고 second[3] = 0이다. ind=3은 4보다 작고 blocks[4] = 6은 blocks[3] = 2보다 크거나 같으니까
3번에서 4번으로 뛸 수 있다
그래서 3번에서 오른쪽으로 뛸 수 있는 최대 거리는 (4번에서 오른쪽으로 뛸 수 있는 최대 거리) + 1로 구해진다
그래서 second[3] = second[4] + 1 = 1이다
마찬가지로 ind=2이면 second[2] = 0인데 ind=2<4이고 blocks[3] = 2, blocks[2] = 5여서 2번에서 3번으로는 못뛴다
그러니까 2번에서 오른쪽으로 뛸 수 있는 최대 거리는 더 이상 뛸 수 없으니까 1이 된다
비슷하게 second[1] = 0에서 blocks[2] = 5, blocks[1] = 5니까 second[1] = second[2] + 1 = 1
second[0] = 0에서 blocks[1] = 5, blocks[0] = 1이니까 second[0] = second[1] + 1 = 2--------------------------------------------------------------------------------------------------------------------------------
여기서 한번 더 생각해봤는데
아니 왼쪽으로 뛸 수 있는 최대거리를 for문을 굳이 오른쪽으로 순회시켜서 구하냐??
오른쪽으로 뛸 수 있는 최대거리를 for문을 왼쪽으로 순회시켜서 구하냐??
이쁘게 왼쪽으로 뛸 수 있는 최대거리를 for문을 왼쪽으로 순회시켜서 못구하냐??
생각을 해보면 오른쪽으로 뛸 수 있는 최대거리를 구하기 위해 for문을 0부터 N-1까지 오른쪽으로 순회시켜보자
blocks = [1,5,5,2,6]이라 가정하고 second[0] = 0, second[1] = 0인데
0번에서 1번으로 뛸 수 있으니까 second[0] = second[1] + 1인데
문제는 이 상황에서 second[1]이 완벽하게 구해지지 않았다는 점이다
그러니까 second[0] 문제를 풀기 위해 second[1]이라는 "이미 푼 부분문제"를 이용해야하는데 "아직 풀지 않은 부분문제"를 이용하니까 못한다는 말
하지만 왼쪽으로 N-1부터 0까지 순회한다면?
그러면 second[4] = 0, second[3] = 0인데 second[4]=0은 지금 완벽하게 푼 문제이고(4번에서는 오른쪽으로 더 이상 못뛰니까)
second[3]을 풀기 위해 3번에서 4번으로 뛸 수 있다는 것을 blocks의 높이로 확인했고
그러니까 second[3] = second[4] + 1 = 1로 풀 수 있다
아무튼 그래서 for문 순회방향이랑 개구리가 뛰는 방향이 반대이다-------------------------------------------------------------------------------------------------------------------------------
그러면 이제 first = [0,0,1,2,0] , second = [2,1,0,1,0]로
각 시작 위치 0,1,2,3,4에서 왼쪽으로 뛸 수 있는 최대 거리와 오른쪽으로 뛸 수 있는 최대 거리를 구했다
그러면 이제 개구리가 각 시작 위치 0,1,2,3,4에서 가장 멀리 떨어지는 최대 거리는 어떻게 찾을까
다시 0부터 N-1까지 순회해서 first와 second를 이용해서 구한다
두 개구리가 최초로 같이 있을때 거리를 1이라고 생각한다
왜냐하면 문제에서 block의 index K>=J일때 K-J+1을 거리라고 했는데 K=J이면 거리가 1이기 때문이다
따라서 왼쪽으로 최대로 뛴 개구리와 오른쪽으로 최대로 뛴 개구리 사이 거리는

위 그림과 같이 왼쪽으로 최대로 뛴 거리 + 오른쪽으로 최대로 뛴 거리 + 1이다
각 시작위치 ind에 대하여 왼쪽으로 뛴 최대거리는 first[ind]이고 오른쪽으로 뛴 최대거리는 second[ind]이므로
각 distance = first[ind] + second[ind] + 1로 구할 수 있다
for ind in range(N):
distance.append(first[ind]+second[ind] + 1)
distance list에 거리를 전부 넣고 이들의 최댓값 max(distance)를 return하면 끝
def solution(blocks):
# write your code in Python 3.6
N = len(blocks)
max_distance = 0
distance = []
first = {}
second = {}
#first frog
for ind in range(0,N):
first[ind] = 0
if ind >0 and (blocks[ind-1] >= blocks[ind]):
first[ind] = first[ind-1] + 1
#second frog
for ind in range(N-1,-1,-1):
second[ind] = 0
if ind < N-1 and (blocks[ind+1] >= blocks[ind]):
second[ind] = second[ind+1] + 1
for ind in range(N):
distance.append(first[ind]+second[ind] + 1)
return max(distance)
이렇게 하면 0초만에 20만개 blocks도 정답을 도출할 수 있다
5. 되돌아보기
이거 다이나믹 프로그래밍 연습 해야겠지??
핵심 아이디어는 상당히 잘 파악했다
두 개구리 사이 거리가 최대가 될려면 개구리 하나는 왼쪽으로 뛰고 다른 개구리는 오른쪽으로 뛰면 된다
이걸 시작 위치 0부터 N-1까지 순회해봐서 최대로 벌어지는 거리를 찾는다
하지만 이걸 효율적으로 해결하려면? 이게 2% 모자랐다
다이나믹 프로그래밍이 교묘하게? 숨겨져있을 줄은
0번에서 오른쪽으로 뛸 수 있는 최대거리는 결국 1번으로 뛸 수 있다면
"(1번에서 오른쪽으로 뛸 수 있는 최대거리)+1"이고 1번으로 뛰지 못한다면 0이다
1번에서 오른쪽으로 뛸 수 있는 최대거리를 이미 구했다면 0초만에 답을 찾을 수 있다는 점
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 다이나믹 프로그래밍 정복기4 - 규칙을 찾으면 되는 쉬운문제들1- (0) | 2022.09.09 |
|---|---|
| 다이나믹 프로그래밍 - Kadane algorithm (0) | 2022.09.04 |
| 다이나믹 프로그래밍 정복기 2 - 연습문제 1로 만들기 - (0) | 2022.09.03 |
| 다이나믹 프로그래밍 정복기1 - 기본이론 - (0) | 2022.09.01 |
| 동적계획법이란 무엇인가? (0) | 2022.01.05 |

