1. 문제
https://www.acmicpc.net/problem/1912
1912번: 연속합
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
www.acmicpc.net
주어진 n개의 임의의 수열에서 1개 이상의 연속된 부분 수열을 선택할 때, 가장 큰 합을 출력
2. 나의 풀이
단순한 규칙, 점화식으로는 풀기 어렵다
메모리, 시간제한 문제로 $O(N^2)$으로도 통과하기 어렵다
처음에 i번째부터 j번째까지 수열의 합을 dp[i][j]에 저장해서 테이블을 완성하려고 했는데
n의 최대가 100000이라 10만*10만 만들자 마자 메모리 초과
from sys import stdin
n = int(stdin.readline())
dp = [[0]*n for _ in range(n)]
num_list = list(map(int,stdin.readline().split()))
max_num = -1000*(100000)
for i in range(n):
dp[i][i] = num_list[i]
if max_num < dp[i][i]:
max_num = dp[i][i]
for i in range(n):
for j in range(i+1,n):
dp[i][j] = dp[i][j-1]+num_list[j]
if max_num < dp[i][j]:
max_num = dp[i][j]
print(max_num)
근데 가능해도 시간초과로 안될 것 같음
그래서 일차원 배열로 해결해야한다
예를 들어 10,-4,3,1 4개만 생각해보자

0개만 보면, 10이 당연히 최대
10과 -4만 보면... 2가지 경우를 비교해야한다
10 + (-4)랑 -4를 비교해서 최댓값은 6
그러면 10이 최대니까 10만 고려하는게 아니라.. 연속되는 부분수열을 구하는거고, 앞으로도 10보다 큰 부분수열이 나올 수 있기 때문에
10을 빼고 -4만 고려하는게 아니라 10,-4를 모두 고려하는게 적절하다.
그리고 10과 -4를 더한 6을 저장해놓는 것이다
다시 3개를 생각해보면
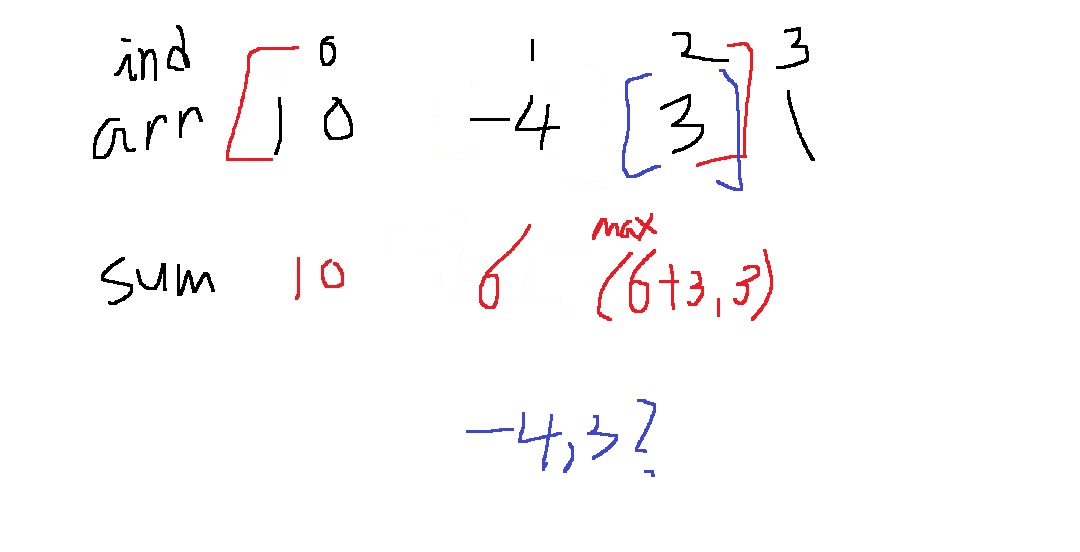
10,-4까지 고려하는게 지금 최선이니까,
10,-4,3을 고려하냐
3만을 고려하냐
두가지 선택지가 있다
-4,3은 고려하면 안되는 것인가? 이전에 -4만 고려하는게 아니라, 10,-4를 고려하자고 했기때문에 -4,3은 고려하는게 아니다
아무튼 이전에 더해놓은 6에 3을 더한 9와 6을 더하지 않은 3을 비교해서 최댓값은 9니까 9를 따로 저장
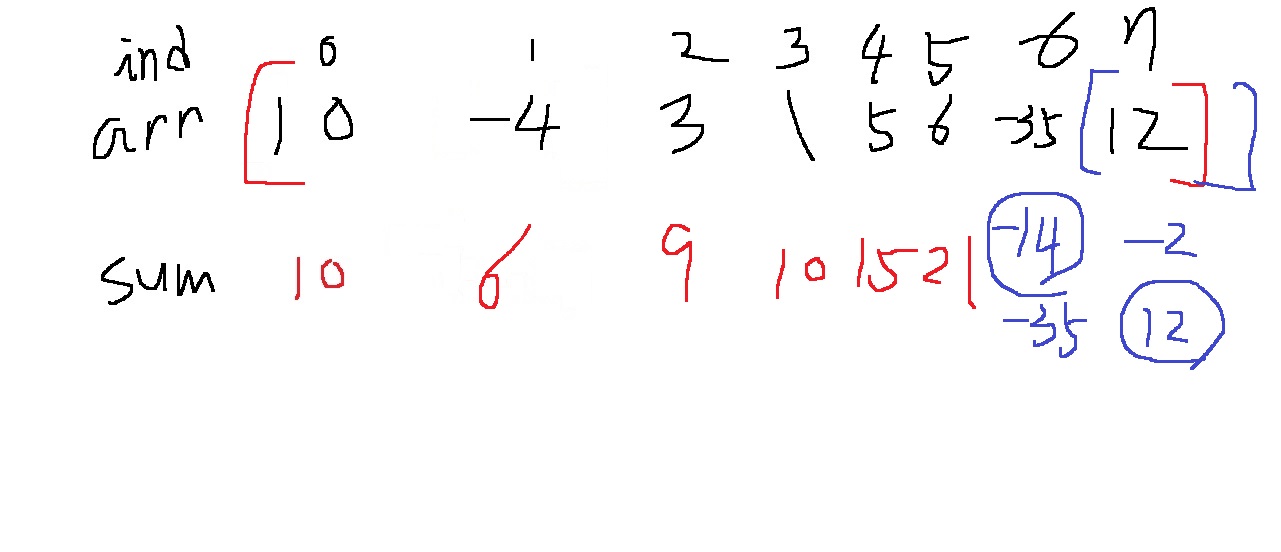
이런 방식으로 접근할 때, 6번째 원소까지는 -14를 저장하게 되는데
7번째 원소 12에 와서는 이제 지금까지 구해놓은 최대경우 10~-35까지의 합인 -14에 대하여
10~12까지 더한 -14+12 = -2와 그냥 12만을 비교해서 12가 더 크니까 12로 갱신해서 저장한다
0번부터 7번까지의 합을 고려하는게 아니라
앞으로는 7번부터 고려하겠다는 의미가 된다
쉽게 생각해서 dp table에는 현재 index i를 기준으로
이전까지의 연속합중 최댓값인 dp[i-1]에 지금 수 arr[i]를 더했을 때 최대가 되느냐?
아니면 arr[i]만 고려하는게 최대가 되느냐?
처음에는 0~(i-1)까지 고려하다가 arr[i]만 고려하는게 최대이면 i번부터 n번까지 고려하게 되는 것이다.
근데 10,-4,3,... 하다가 처음에 10이 최대인데, 10-4하면 6은 10보다 작으니까.. 10으로 여전히 저장해야하느냐?
근데 그렇게 하면 연속 부분수열이라는 조건에 어긋나게 된다는 것임
그래서 10보다 10-4를 고려하는게 낫다. 왜냐하면 계속 더했을때 앞으로 10보다 더 커질 수 있으니까
from sys import stdin
n = int(stdin.readline())
num_list = list(map(int,stdin.readline().split()))
dp = [0] * n
dp[0] = num_list[0]
max_num = dp[0]
for i in range(1,n):
dp[i] = max(dp[i-1]+num_list[i],num_list[i])
if dp[i] > max_num:
max_num = dp[i]
print(max_num)
크기 n만큼의 dp table을 만들고
초기 dp[0] = num_list[0]를 만든 다음에 현재 최댓값 max_num은 dp[0]니까 이것으로 초기화
1번부터 n-1까지 순회하여
dp[i-1] + num_list[i]와 num_list[i]중 최댓값을 비교하여 dp[i]에 저장
저장할때마다 max_num을 계속 갱신해준다
for문이 끝나면 max_num 출력
3. Kadane algorithm
전체 배열 A에서 모든 연속하는 부분 배열중 가장 큰 합을 구하는 문제
배열 A가 A = [2,1,-4,3,4,-4,6]이라고 하자.
인덱스 i = 3을 기준으로 모든 연속하는 부분 배열의 합은..
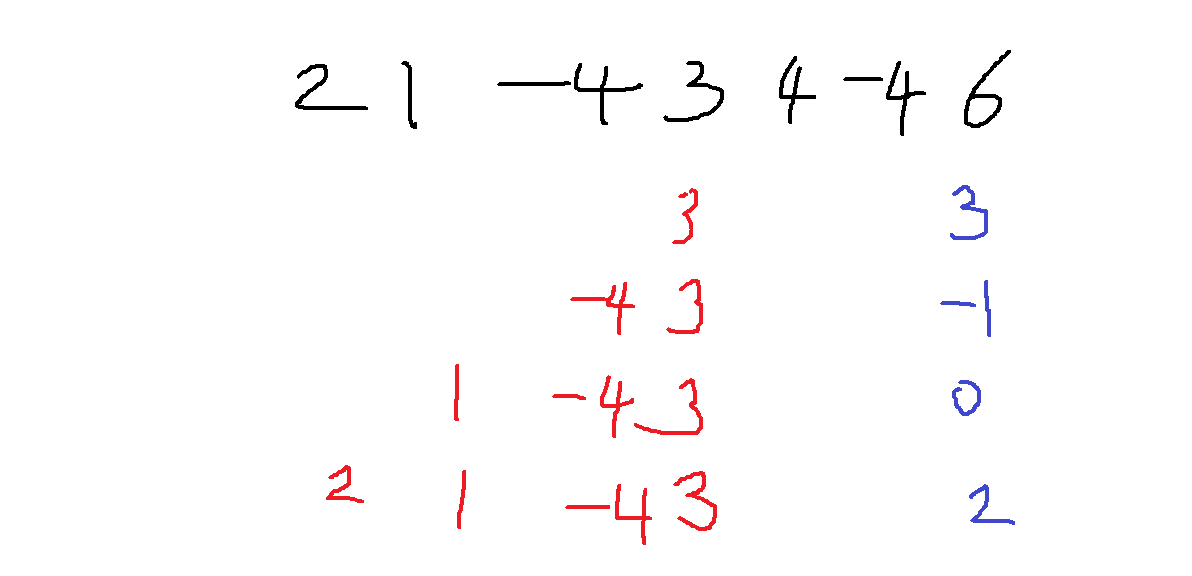
만약 인덱스 i = 4에서 부분배열의 합은..

인덱스 3번째 수까지 합 3,-1,0,2를 안다면 인덱스 4번째 수 4를 더해서 i번째 수까지 합은 7,3,4,6임을 알 수 있다.
또한 인덱스 4번째 수 4도 4번째 수까지 연속 부분 배열의 합 중 하나이다.
즉 인덱스 4번째 수 4와 인덱스 3번째 수까지 합에 4를 더한 7,3,4,6중 가장 큰 값이 인덱스 4번째 수까지 가장 큰 연속하는 부분 배열의 합이 된다.
그러므로 인덱스 i-1번째 수까지 합을 안다면, 인덱스 i번째 수를 더해서 i번째 수까지 합을 구할 수 있다.
따라서 인덱스 i-1번째 수까지 봤을 때 가장 큰 합을 알고 있다면, i번째 수까지 가장 큰 합도 알 수 있다.
dp[i] = i번째까지 가장 큰 연속 부분 합
dp[i] = max(A[i], dp[i-1] + A[i])
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 다이나믹 프로그래밍 정복 -피보나치 변형 몇가지- (0) | 2022.09.20 |
|---|---|
| 다이나믹 프로그래밍 정복기4 - 규칙을 찾으면 되는 쉬운문제들1- (0) | 2022.09.09 |
| 다이나믹 프로그래밍 정복기 2 - 연습문제 1로 만들기 - (0) | 2022.09.03 |
| 다이나믹 프로그래밍 정복기1 - 기본이론 - (0) | 2022.09.01 |
| 다이나믹프로그래밍 - 어떻게하면 완전탐색도 더 효율적으로 할 수 있을까? (0) | 2022.06.23 |

