1. 문제
https://programmers.co.kr/learn/courses/30/lessons/42839
코딩테스트 연습 - 소수 찾기
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다. 각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이
programmers.co.kr
한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.
각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이조각으로 만들 수 있는 소수가 몇개인지 return하도록 solution 함수를 완성해주세요.
2. 제한사항
numbers는 길이 1 이상 7 이하인 문자열
numbers는 0~9까지 숫자만으로 이루어져 있습니다.
"013"은 0,1,3 숫자가 적힌 종이 조각이 흩어져있다는 의미
3. 입출력 예시

4. 나의 풀이
주어진 숫자들로 만들 수 있는 모든 숫자들을 생각하고 이 숫자들중 소수가 무엇인지 검사하는 방식으로 구성
itertools의 permutations라는 함수는 리스트를 받아 이들로 만들 수 있는 순열을 내준다
def solution(numbers):
answer = 0
from itertools import permutations
numbers_list = list(numbers)
total_len = len(numbers)
prime_set = set()
문자열 numbers를 list(numbers)하면 각 문자 하나씩을 원소로 하는 리스트로 변환
prime_set = set()으로 하는 것은 중복된 소수가 있을 수 있어서 set()으로 미리 만들었다
total_len = len(numbers)로 미리 구해서 어차피 numbers의 길이만큼 permutations를 구해야해서 나중에 시간을 줄인다
for i in range(1,total_len+1):
permut_list = list(permutations(numbers_list,i))
그러면 1부터 문자열의 길이 total_len만큼 i로 두어서 numbers_list에 대한 permutation 리스트를 구한다
"17"을 예로 들면 ['1','7']이 numbers_list이고
i=1이면 permutations는 '1', '7'
i=2이면 permutations는 '1','7', '7','1'
[('1',), ('7',)]
[('1', '7'), ('7', '1')]
각 i에 대해서 permut_list를 for문을 이용해 순회한다
받아온 permut은 위와 같이 튜플로 되어있어서
''.join(permut)을 하면 문자열로 합칠 수 있다
for i in range(1,total_len+1):
permut_list = list(permutations(numbers_list,i))
for permut in permut_list:
num = int(''.join(permut))
여기서 중요한 점은 합친 문자열을 int()로 씌우면 정수형으로 바뀐다
여기서 중요한 점은 입출력 예시에서 11과 011은 같은 숫자로 취급한다고 했는데 이러한 점을 고려할 수 있다
int('11')은 11이고 int('011')도 int('0011')도 11이 된다
이제 숫자로 바꾼 값이 소수인지 판별한다
for i in range(1,total_len+1):
permut_list = list(permutations(numbers_list,i))
for permut in permut_list:
num = int(''.join(permut))
prime = True
if num >= 2:
for a in range(2,num):
if num % a == 0:
prime = False
break
if prime:
prime_set.add(num)
prime= True로 일단 지표를 두고
1은 소수가 아니니까 num >= 2만 고려한다
소수는 "1과 자기자신"으로만 나누어 떨어지는 수
그러면 1과 num은 당연히 나누어 떨어지니까
2부터 num-1까지 주어진 num을 나눠서 나머지가 0인지 아닌지 검사해본다
만약 나머지가 0인 경우가 1번이라도 발생하면 prime=False로 주고 즉시 break해서 for문을 탈출
for문을 탈출하고 나서도 prime = True이면 num은 소수니까 prime_set.add()로 num을 추가
prime= False면 num은 소수가 아니니까 추가하지 않는다
마지막으로 prime_set의 길이를 answer로 출력하면 끝
answer = len(prime_set)
return answer
5. 소수를 판별하는 알고리즘
소수 판별 검사하는 알고리즘에서 시간을 줄이는 방법은 2부터 num-1까지 검사하는 것이 아니라
num의 제곱근까지 검사하면 된다는 점이다.
------------------------------------------------------------------------------------------------------------
왜 그런지 생각해보자
간단하게 num=100의 약수는 1, 2, 4, 5, 10, 20, 25, 50, 100이 있다
이 때 100이 소수인지 아닌지 검사하고자 한다면 100을 1부터 100까지 하나씩 돌아가면서 나눠보면 된다
이 때 나누어 떨어지는 수가 1과 100만 있으면 이 수는 소수이다.
그런데 100은 1과 100으로 당연히 나누어 떨어지기 때문에 굳이 검사하지 않아도 된다.
그래서 2부터 99까지 검사한다.
근데 1, 2, 4, 5, 10, 20, 25, 50, 100 이 수열을 다시 확인해보면
100이 2로 나누어 떨어진다면, 50으로는 당연히 나누어 떨어지기 때문에 2로 나누어 떨어지는지만 확인하면 된다.
100이 4로 나누어 떨어진다면 25로는 당연히 나누어 떨어지기 때문에 4로 나누어 떨어지는지만 확인하면 된다.
100이 5로 나누어 떨어진다면 20으로는 당연히 나누어 떨어지기 때문에 5로 나누어 떨어지는지만 확인하면 된다
즉 어떤 자연수의 약수들의 배열은 대칭적으로 이루어져 있다
즉 (1,100) , (2,50), (4,25), (5,20), (10,10)
대칭이 되는 10은 어디서 나온 수인가?? 100의 제곱근이다.
그래서 100이 소수인지 확인하기 위해서 2부터 10까지 나누어 떨어지는 수가 있는지 확인해보면 된다
------------------------------------------------------------------------------------------------------------------------------
일반적으로 임의의 자연수 A = a * b가 된다면 a와 b는 A의 약수니까 당연히 A보다는 작다.
그런데 a와 b가 모두 sqrt(A)보다 클 수는 없다
무슨 말이냐면 a>sqrt(A)이면 반드시 b<sqrt(A)이고 반대로 a<sqrt(A)이면 반드시 b>sqrt(A)이다.
이에 더해 a=sqrt(A)이면 반드시 b=sqrt(A)가 된다.
그래서 sqrt(A)를 기준으로 작은 수에서 A에 대해 나누어떨어지는 수가 있다면 큰 수에서 당연히 나누어 떨어지는 수가 존재하고
반대로 sqrt(A)보다 작은 수에서 A에 대해 나누어떨어지는 수가 없다면 당연히 큰 수에서도 나누어 떨어지는 수는 찾아볼 수가 없다
에라토스테네스의 체 혹은 소수판정 시 제곱근 까지만 확인하면 되는 이유
흔히 에라토스테네스의 체를 사용해 n 이하의 모든 소수를 구하려고 할 때, 효율적으로 구하기 위해 n의 제곱근( sqrt(n) ) 까지만 확인하곤 한다. 1년전쯤엔 n까지 다 확인하거나, 좀 머리 쓴다고 n/
nahwasa.com
------------------------------------------------------------------------------------------------------------------------------
for i in range(1,total_len+1):
permut_list = list(permutations(numbers_list,i))
for permut in permut_list:
num = int(''.join(permut))
prime = True
if num >= 2:
for a in range(2,int((num**(1/2)))+1): ############ num >> int((num**(1/2)))+1
if num % a == 0:
prime = False
break
if prime:
prime_set.add(num)
그러면 위에서 2부터 num-1까지 검사하는 알고리즘을 2부터 num의 제곱근까지 검사하는 알고리즘으로 고친다
제곱근은 sqrt 함수를 쓰는게 아니라 num**(1/2)를 사용하면 된다
여기서 num**(1/2)가 자연수가 아닐 수 있어서 int((num**(1/2)))로 정수화 시킨다
이 때 int((num**(1/2)))면 num의 제곱근-1까지 검사하므로 오류가 생길 수 있다
왜냐하면 num=100이면 10까지 검사해봐야하는데 9까지 검사하니까
그래서 int((num**(1/2)))+1을 해서 num의 제곱근까지 검사해줘야한다
2부터 num-1까지 검사하면

2부터 num의 제곱근까지 검사하면

의미있게 시간차이가 난다
6. 다른 풀이
에라토스테네스의 체를 이용해서 소수 판별을 할 수 있다.
이게 조금 더 빠르다는데
<알고리즘>
자연수 n이하의 수에서 소수들을 찾고자 하는 알고리즘
1) 가능한 소수 후보 1부터 n까지의 수열을 저장
2) 1은 소수가 아니니까 1을 제거
3) 2를 남기고 2의 배수를 모두 제거
4) 3을 남기고 3의 배수를 모두 제거
<4는 2의 배수에서 제거됨>
5) 5를 남기고 5의 배수를 모두 제거
<6은 3의 배수에서 제거됨>
6) 7을 남기고 7의 배수를 모두 제거
<8은 2,4의 배수에서 제거됨>
<9는 3의 배수에서 제거됨>
<10은 2,5의 배수에서 제거됨>
7)11을 남기고 11의 배수를 모두 제거
.......
위 과정을 더 이상 할 수 없을 때까지 계속 수행
----------------------------------------------------------------------
여기서 시간을 더 줄이기 위해 제곱근 판별법이랑 응용을 해보면
자연수의 최대 약수는 제곱근까지니까
1) 가능한 소수 후보 1부터 n까지의 수열을 저장
2) 1은 소수가 아니니까 1을 제거
3) 2를 남기고 2의 배수를 모두 제거
4) 3을 남기고 3의 배수를 모두 제거
<4는 2의 배수에서 제거됨>
5) 5를 남기고 5의 배수를 모두 제거
<6은 3의 배수에서 제거됨>
6) 7을 남기고 7의 배수를 모두 제거
<8은 2,4의 배수에서 제거됨>
<9는 3의 배수에서 제거됨>
<10은 2,5의 배수에서 제거됨>
7)11을 남기고 11의 배수를 모두 제거
........
8)sqrt(n)의 배수를 모두 제거
sqrt(n)의 배수까지만 검사하면 된다
--------------------------------------------------------
def solution(numbers):
from itertools import permutations
answer = 0
numbers_list = list(numbers)
total_len = len(numbers)
num_set = set()
for i in range(1,total_len+1):
permut_list = list(permutations(numbers_list,i))
for permut in permut_list:
num = int(''.join(permut))
if num >= 2:
num_set.add(num)
max_num = max(num_set)
for a in range(2,int((max_num**(1/2)))+1):
num_set -= set(range(2*a,max_num+1,a))
answer = len(num_set)
return answer
문자열로부터 얻은 가능한 수의 후보를 num_set에 저장을 시켜
이 때 0이나 1은 소수가 아니니까 num>=2이면 num_set에 저장을 시키도록 함
17이면 num_set = {7,17,71}이 나오겠지
011이면 num_set = {10,11,101,110}이 나오겠지
그러면 num_set의 최댓값을 찾고 그것의 제곱근을 찾아
예를 들어 {1,7,17,71}은 71이하의 자연수 중에서 소수를 찾는 문제와 같고
제곱근 판별법에 의해 약수 최댓값이 sqrt(71)이니까 sqrt(71)의 배수까지만 걸러내면 된다
for a in range(2,int((max_num**(1/2)))+1):
num_set -= set(range(2*a,max_num+1,a))
그러면 2부터 max_num의 제곱근까지 배수의 집합을 어떻게 만들까???
range함수를 이용하면 된다
range( <start>, <end>, <step>)을 이용해서 <start>부터 <end>-1까지 <step>씩 건너 뛰어서 수열을 만든다
set(range(2*a,max_num+1,a)) 이렇게 하면 에라토스테네스 체 알고리즘에서 "a는 남기고 a의 배수를 걸러낸다"라고 했으니까
2*a부터 max_num까지 a씩 건너 뛰어서 수열을 만든다
{2*a, 3*a, 4*a, ...., k*a<max_num}로 만들어질 것이다
이것을 num_set 집합에 빼주면 차집합이 구해진다
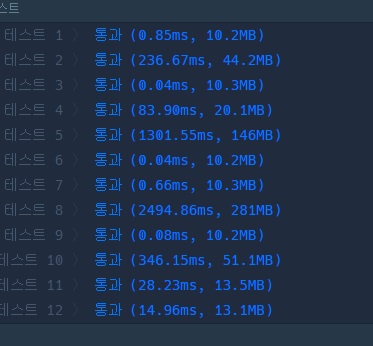
배수집합을 생성하니까 좀 느려지는듯???
검사해야할 후보가 {10,11,101,110}같이 작아서 오히려 단순 제곱근 판별법보다 더 느려지는듯
7. 되돌아보기
나름 잘 풀었다
소수 판별할 때 제곱근 판별법 잘 기억해두자고
num이하의 수를 하나씩 돌아가면서 나누어보는데 num의 제곱근까지만 검사하면 된다고
마지막 풀이에서 배수 집합 만들때
range(a, max+1, a)로 a의 배수집합 만들 수 있고
중복을 미리 제거하기 위해 set()을 이용할 수 있다는 점
차집합 계산 - 그냥 하면 된다는 점
'정수론' 카테고리의 다른 글
| 소인수분해 기본 알고리즘 배우기 (0) | 2022.12.13 |
|---|---|
| 정수론 - 합과 곱은 왜 계속 나눠도 문제가 없는가? - (0) | 2022.09.09 |
| 소수를 빠르게 구하는 에라토스테네스의 체 알고리즘 (0) | 2022.09.07 |
| 이항계수를 구하는 알고리즘 고급편 - 페르마의 소정리- (0) | 2022.08.16 |
| 최대공약수를 빠르게 구하는 알고리즘 - 유클리드 호제법 (0) | 2022.08.10 |

