1. 문제
11653번: 소인수분해
첫째 줄에 정수 N (1 ≤ N ≤ 10,000,000)이 주어진다.
www.acmicpc.net
2. 소인수분해 하는 방법?
어렵게 생각할 필요 없이 사람이 소인수 분해를 어떻게 하는지 생각해보자.
100을 소인수분해 한다고 해보자.
암산으로 5*20 >>> 5*4*5 >> 5^2 * 2^2이 나오기는 하는데...
이게 어떻게 이루어지는가??? 처음부터 생각해보자.
소인수분해는 소수들의 곱이다.
그러니까 소수의 최솟값인 2부터 시작해서 주어진 수 100을 나눠보면 된다.
만약에 100이 2로 나누어진다면?
100 = 2 * 50이다.
그러면.. 우리는 어떤 걸 이제 나누어보는가? 100을 2로 나누고 나온 몫인 50을 다시 2로 나누어본다.

그러면.. 50 = 2 * 25
다시 50이 2로 나누어 떨어지므로... 그 몫인 25를 다시 2부터 시작해서 나누어본다.
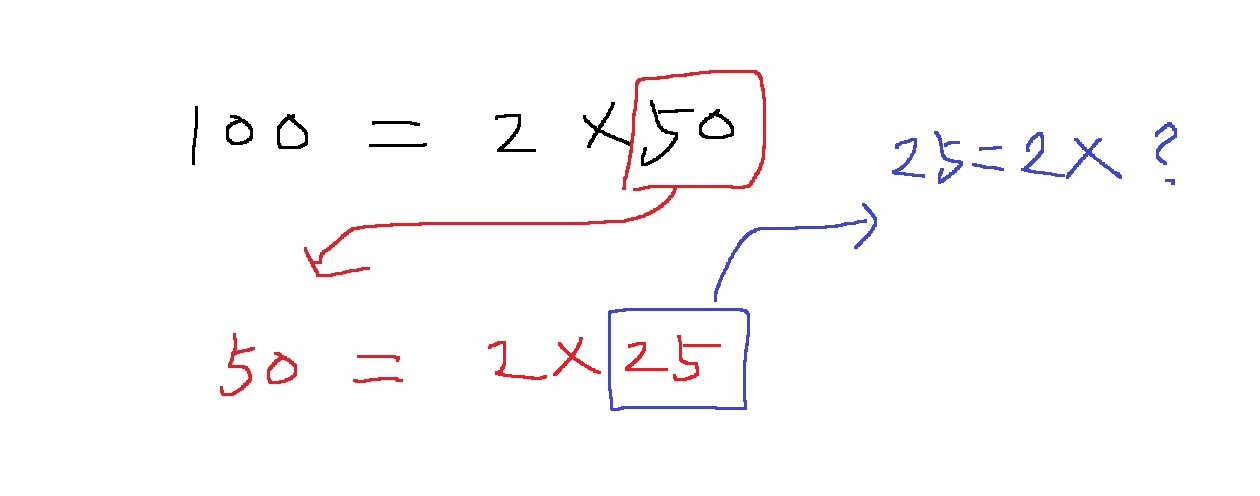
그런데 25는 2로 나누어 떨어지지 않는다.. 그러면 어떻게 하는가?
100 = 2 * 2 * 25이고.. 2가 소인수라는 것을 알아냈다.

그리고 2에 1을 더해서 3으로 나누어본다.
3으로도 나누어 떨어지지 않는다.
3+1 = 4로 나누어본다.

4로도 나누어 떨어지지 않는다. (사실 4로 나누어 떨어진다면... 4를 인수로 가지는데.. 그렇다면 이전에 2로 나누어 떨어졌어야 했다)
4+1 = 5로 나누어본다.
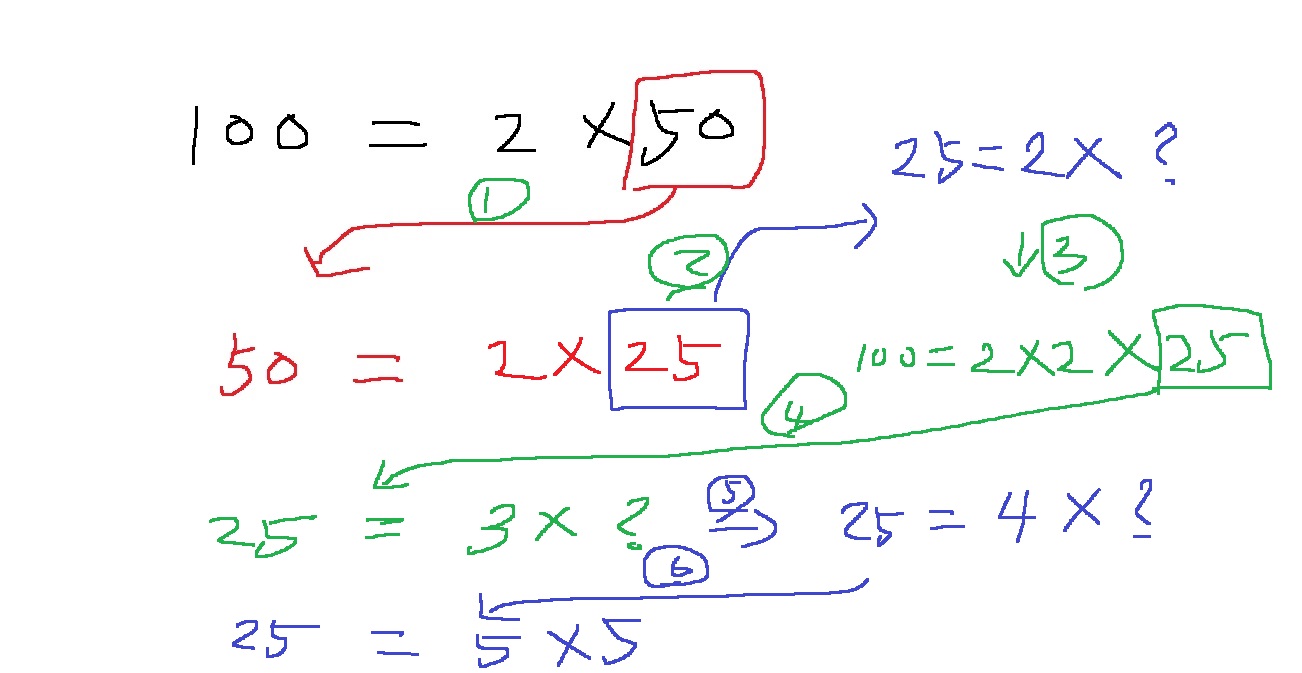
25는 5로 나누어 떨어진다.. 즉 25 = 5 * 5
그리고 5를 다시 5로 나누어본다.. 5로 나누어 떨어진다
그래서 5 = 5 * 1이다.
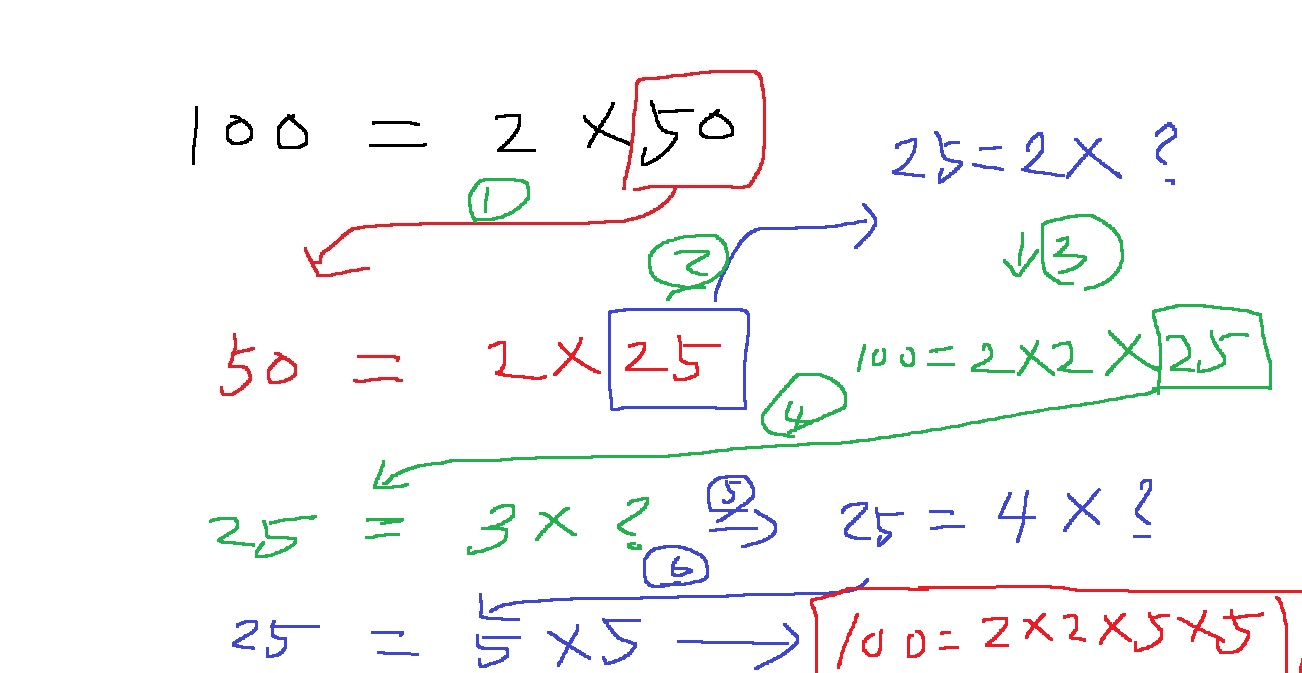
마지막이 1이다. 그러므로 100을 소인수분해하면.. 100 = 2 * 2 * 5 * 5이다.
3. 기본 알고리즘
그러므로 주어진 수 n을 소인수분해하는 기본 알고리즘은 다음과 같을 것이다.
3-1) p = 2부터 시작한다.
3-2) $p^{2}$이 n이하일때 3-3),3-4) 반복을 수행한다.
(왜냐하면.. n이 나누어 떨어지는 정수의 최댓값은 $\sqrt{n}$이기 때문..
소수 판정에서 $\sqrt{n}$까지 검사해보는 이유와 동일하다.
이젠 너무 유명하니 자세한 설명은 쓰지 않는다)
3-3) n이 p로 나누어 떨어지면 p는 n의 소인수이고, n을 p로 나눈 몫으로 n을 갱신
3-4) 나누어 떨어지지 않는다면, p를 1 증가시킨다.
3-5) 만약 반복문을 탈출했는데 n이 1보다 클 경우, n도 소인수이다.
---------------------------------------------------
3-6) 그런데, n > 1인데 n이 소수일수가 있다.
그러니까 n이 그냥 처음부터 소수인 경우를 생각해보자.
그런 경우에 반복문을 돈다고 생각해보자..
예를 들어 n = 13이면... p = 2일때.. 4 <= 13인데..
2,3,4 까지 나누어 떨어지지 않다보니까...
반복문을 수행하지 않고 n = 13인데..
그러면 n = 13은 그 자체로 소수가 된다.
from sys import stdin
n = int(stdin.readline())
p = 2
#최대로 나누어 떨어지는 정수는 n**(1/2)
while p*p <= n:
if n % p == 0:
n = n//p
print(p) #n이 p로 나누어 떨어지면, p는 소인수
else:
p += 1
#반복문 탈출 후에, n > 1이면.. n은 소인수
if n > 1:
print(n)
기본문제에도 분명 배울게 있다..
브론즈1이지만... 알고리즘이 생각 안난거 실화냐?
'정수론' 카테고리의 다른 글
| 페르마의 소정리 문제 풀어보면서 익히기 (0) | 2022.12.15 |
|---|---|
| 오일러의 phi 함수 직접 구현해보면서 개념 익히기 (0) | 2022.12.13 |
| 정수론 - 합과 곱은 왜 계속 나눠도 문제가 없는가? - (0) | 2022.09.09 |
| 소수를 빠르게 구하는 에라토스테네스의 체 알고리즘 (0) | 2022.09.07 |
| 이항계수를 구하는 알고리즘 고급편 - 페르마의 소정리- (0) | 2022.08.16 |

