유사도와 거리는 밀접한 관계가 있다고 생각할 수 있다.
거리가 클 수록 유사도는 떨어진다. 비교하는 특징은 같으나 측량하는 관점에서는 서로 반대라는 것이다.
두 데이터 X,Y의 거리함수(distance function) d는 수학적으로 다음과 같이 정의한다.
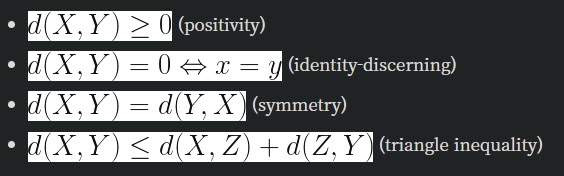
위 식을 모두 만족하는 d가 거리함수다
유사도함수 s(X,Y)는 실수값을 출력하는 함수로 특별한 정의는 없다. 그래서 조금 더 일반적이다(general)
유사도함수가 특별히 [0,1]내에서 값을 가진다고 하면 두 함수 의미의 서로 반대의미와 identity-discening에 주목하여

유사도함수가 위의 거리함수의 공리를 모두 만족한다면 완벽하게 혼용해서 사용할 수 있다.
그런데 모든 유사도함수가 위의 조건을 만족할까? 그렇지도 않다.
지금 당장 생각나는 예시는 KL divergence로 두 분포의 차이를 설명하는 지표지만 대칭성을 만족하지 않아 거리는 아니라고 배웠다.
다음으로 cosine similarity라고 부르는 두 벡터 사이의 코사인 유사도는 거리함수가 될 수 있을까?

cosine similarity는 두 벡터 사이의 각으로 유사성을 측정하고 cosine distance는 절대적인 거리차이이다.
cosine distance는 많은 경우 다음과 같이 정의한다.

cosine이 [0,1]에서 mapping되기때문에 (두 벡터사이의 각도는 2개가 있는데 작은 각을 선택하면 그렇구나)
이것이 진정으로 거리함수인가? 실제로 그렇지 않다 왜냐하면 triangle inequality를 만족하지 않는다고 한다.
많은 경우 triangle inequality를 만족하지 않아서 distance가 되지 않는 경우가 많다고 한다
참고로 자카드 유사도로 구한 자카드 거리는 실제로 거리함수 조건을 만족한다고 한다.

결론으로 코사인 유사도와 코사인 거리는 정확하게는 특성이 같지않다.
그러나 자카드 유사도는 거리함수가 될수 있다. 구별하는것이 중요한것은 아니고 특성을 잘 이해하는 것이 중요하다
-------------------------------------------------------------------------------------------------------------------------------------------------------------
***word embedding vector의 distance
euclidean distance를 많이 쓰고, 때에 따라선 잘 쓰진 않지만 manhattan distance를 쓸 수도 있다.
요즘에는 cosine distance를 많이 쓴다고 한다.
고차원의 word embedding을 사용한다는 것은 2차원의 강력한 시각화 능력을 잃어버린다는 것이지만
코사인 유사도를 계산할 때 많은 차원을 고려하므로 훨씬 좋은 유사도를 제공할 수 있다.
벡터 간의 관련성을 절대적인 거리 관점에서 보는 것이 euclidean distance라고 한다면
두 벡터 간 각도의 차이로 관련성을 보겠다면 cosine distance가 될 것이다.
기본적으로 무슨 distance를 쓸 지는 사용자 마음이다
-----------------------------------------------------------------------------------------------------------------------------
마지막으로 오늘 유클리디안 거리로 intrusion detection에서 납득할 수 없었던 점에 대한 하나의 해답이 될 수 있을 것 같다.
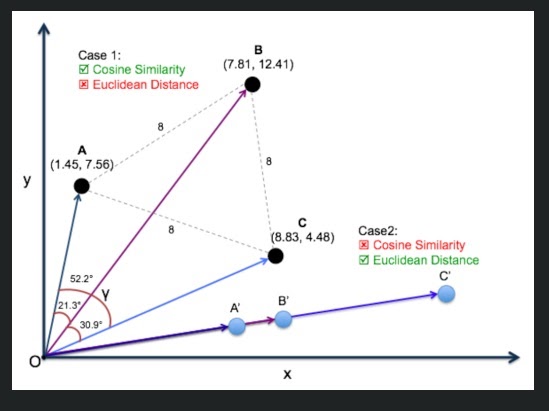
위에서 첫번째 케이스의 A,B,C를 보면 유클리디안 distance로 구하면 모두 동일해서 거리가 동일하니까 세 벡터가 서로 동일하게 유사하다는 결론이 나온다.
분명히 다름에도 불구하고.. 그러나 cosine 유사도로 측정하면 서로 다른 유사도임을 확인할 수 있다.
두번째 케이스는 A’,B’,C’인데 cosine 유사도는 1로 모두 동일해서 비교가 안된다.
분명히 다름에도 모두 동일하다고 나온다. 그러나 유클리디안 거리로 비교하면 절대적인 거리차이를 이해할 수 있게 된다.
상황에 맞게 적절한 함수를 선택하는 것이 중요하다.
참고
https://gritmind.blog/2020/06/21/diff_similarity_distance/
데이터과학에서 유사도와 거리의 차이점
벡터로 표현된 두 개의 데이터를 비교할 때, 비슷한/유사한 정도를 나타내는 용어로 유사도(similarity)와 거리(distance)가 있습니다. 그런데 “두 데이터의 유사도는 어떤가? 거리는 얼마인가?”처
gritmind.blog
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| sequence 데이터를 모델링하는 방법 (0) | 2022.02.11 |
|---|---|
| transfer learning이란 무엇일까? (0) | 2022.02.09 |
| 시대를 뒤흔든 딥러닝의 아이디어들 (0) | 2022.02.05 |
| convolution 연산의 stride와 padding (0) | 2022.02.04 |
| convolution 연산 이해하기 중급편 (0) | 2022.02.03 |

