1. Fully connected 연산
기존의 MLP는 가중치 행렬에서 각 행마다 다른 가중치 행들이 각각 Hidden vector에 연결되는 구조다.
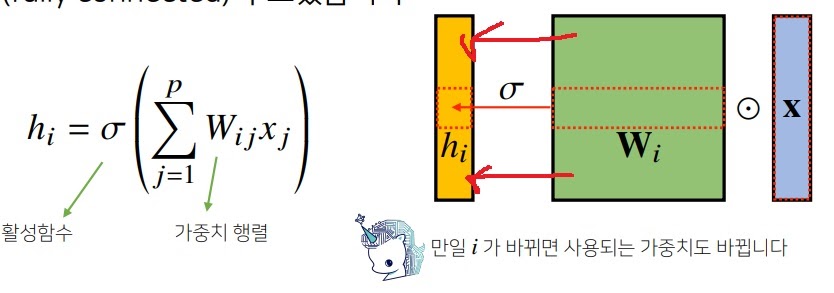
이게 단점은 parameter가 많아서 계산량이 많아진다.
2. Convolution 연산
고정된 가중치 행렬 kernel을 입력벡터상에 움직여가면서 모든 hidden vector에 연결시키는 전략은 어떨까?
parameter 수가 엄청나게 줄어들어 계산이 쉬워진다.
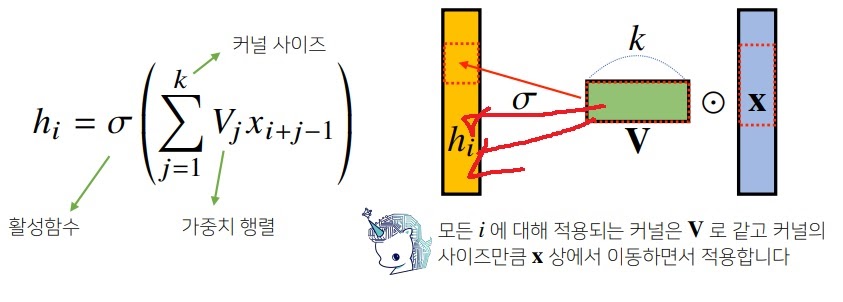
심지어 행렬곱이니까 여전히 선형변환이다.
3. Convolution
함수 공식은 다음과 같다.

참고로 convolution은 변수변환을 시켜서 교환법칙이 성립한다는 것을 보일 수 있다.
커널을 이용해 신호를 국소적으로 증폭 또는 감소시켜 정보를 변환하거나 추출하는 방식으로 signal processing에서 나왔다.
z만 있는 부분이 커널이다. z를 움직여(커널을 움직여)가면서 신호함수를 변화시킴
4. cross correlation
원래 CNN은 Cross correlation연산을 이용한다.

근데 전체공간에서 +나 -나 큰 차이 없어서(컴퓨팅 연산은 큰 차이 있지만) convolution이라 부르다보니 그렇게 굳어졌다함
굳이 차이를 기술하자면
cross correlation이 필터를 input에 그대로 겹쳐놓고 element wise product를 하는 것(일반적으로 아는 CNN연산)이고
convolution연산은 필터를 180도 회전시켜서 합성곱을 수행하는 연산이다.

필터를 180도 회전시켜서 수행되는 것을 확인할 수 있다
5. 그래픽에 의한 convolution 이해
kernel은 정의역 상에서 움직이지만 모두에게 공통으로 쓰는 고정되어있는 값으로(translation invariant)
주어진 신호에 국소적으로 작용하여 변화시킴

6. 다차원에서 convolution연산
1차원 이상도 convolution을 구할 수 있다.
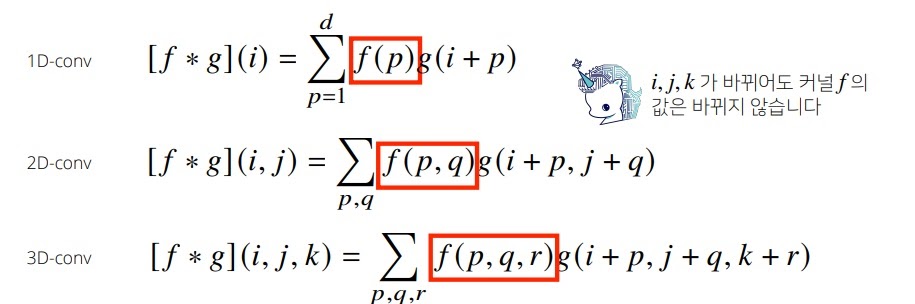
2-d는 보통 흑백? 3-d는 컬러라는데 맞나?
데이터의 성격에 따라 사용하는 커널이 다름
6-1) 2차원 convolution
2차원 convolution 연산은 커널을 입력벡터 상에서 움직여가면서 선형함수와 합성하는 구조이다.

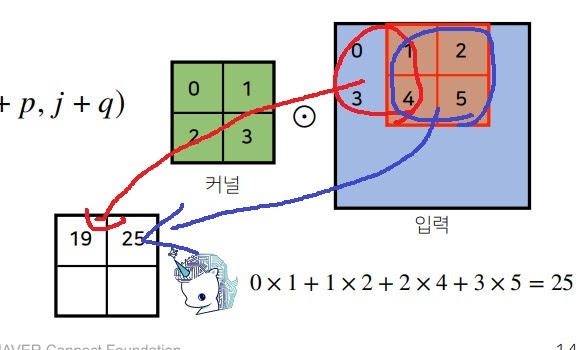
일반적인 output의 공식 외워야하나?? 딱히?? 외울 필요까지는..(1-stride일때임 1칸씩만 움직일때)
위에 그림처럼 어떻게 convolution을 할 수 있느냐를 아는 것이 중요하다

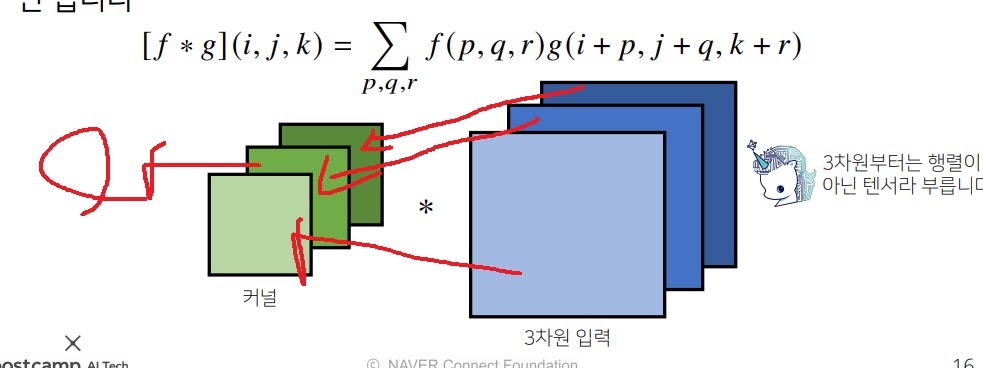
6-2) 3차원 convolution
3차원 convolution은 각 채널마다 convolution을 적용하면 된다.
보통 하나의 값이 나오는데 여러개를 출력(tensor)시키고 싶으면 kernel을 그 만큼 준비하면 된다.
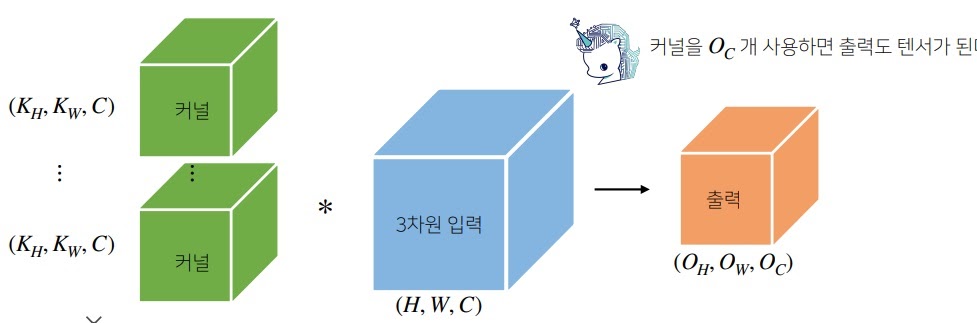
kernel을 여러개 사용하여 입력을 하면 출력도 tensor로 나옴
참고
https://metamath1.github.io/cnn/index.html
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| convolution 연산의 stride와 padding (0) | 2022.02.04 |
|---|---|
| convolution 연산 이해하기 중급편 (0) | 2022.02.03 |
| backpropagation의 개괄적인 설명 (0) | 2022.01.26 |
| 여러가지 cross validation 방법들 (0) | 2022.01.17 |
| 확률적 경사하강법(stochastic gradient descent method) (0) | 2022.01.04 |

