그래프에서 최단경로를 탐색하는 알고리즘
특정 하나의 node에서 다른 모든 node로 가는 최단 경로를 알려줌
link의 가중치가 음수인 경우는 고려하지 않음
하나의 최단 거리를 그 이전까지 구했던 최단 거리 정보를 사용하여 구함
---------------------------------------------------------------------------------------------------------------------
1. 출발노드를 설정
2. 출발 노드를 기준으로 각 노드의 최소 비용을 저장
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신
5. 위에서 3.과 4.번을 반복
--------------------------------------------------------------------------------------------------------------------
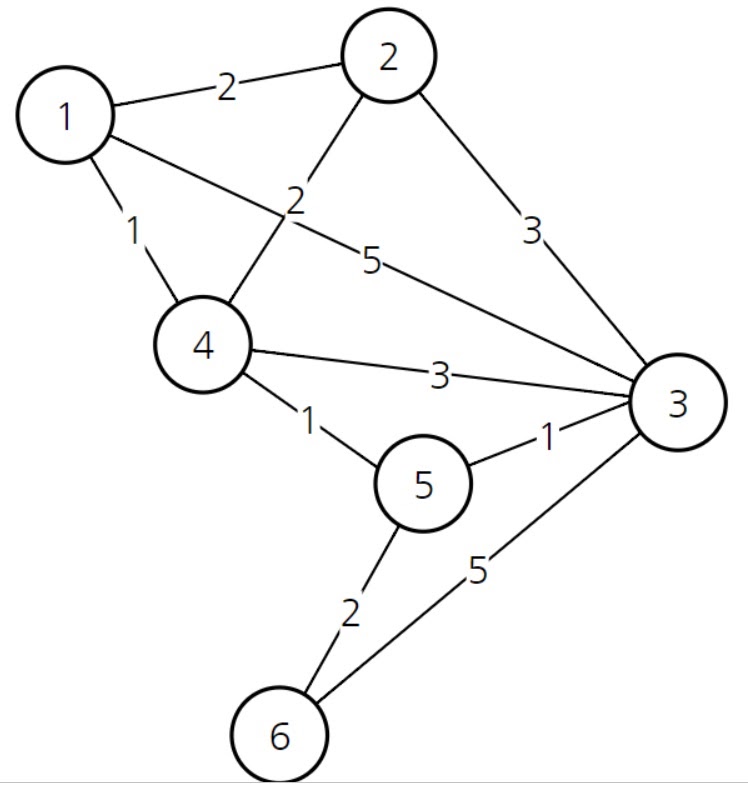
위 그림과 같은 그래프가 주어질 때
1번에서 다른 노드로 가는 최단 경로를 구하고자 함

현재 1번 노드를 선택하면 다른 노드까지 가는 비용이 위와 같음
1번 노드는 2번, 3번, 4번 노드와 직접 연결되어 있고
5번, 6번 노드와는 직접 연결되어 있지 않아서 5번,6번 노드로 가는 비용은 현재 무한대
1번에서 1번으로 가는 경우는 비용이 0이니 어차피 선택할 필요도 없고
이 상태에서 가장 비용이 적은 노드인 4번을 선택함

이 때 1번에서 4번을 반드시 거쳐서 2번, 3번, 5번, 6번 노드로 가는 최소 비용을 구하여 배열을 갱신함

그러면 1번에서 4번을 거쳐 3번으로 가는 비용이 4이고
1번에서 3번을 가는 비용 5보다 작으므로 배열에서 3번 index 부분을 4로 갱신하고
1번에서 4번을 거쳐 5번으로 가는 경우 비용이 2이기 때문에 원래 무한보다 작으므로 새롭게 갱신한다
4번은 고려했으므로 freeze시킴
다음으로 현재 비용이 가장 작은 2번 노드를 선택함

이 경우 1>2>3으로 가면 비용이 5라서 이전 비용 4보다 크고
1>2>4>5나 1>2>3>5도 원래 비용 2보다 비싸므로 배열을 갱신하지 않고
2번 node만 freeze시킨다

이제 방문하지 않은 노드중 비용이 가장 싼 5번 노드를 선택
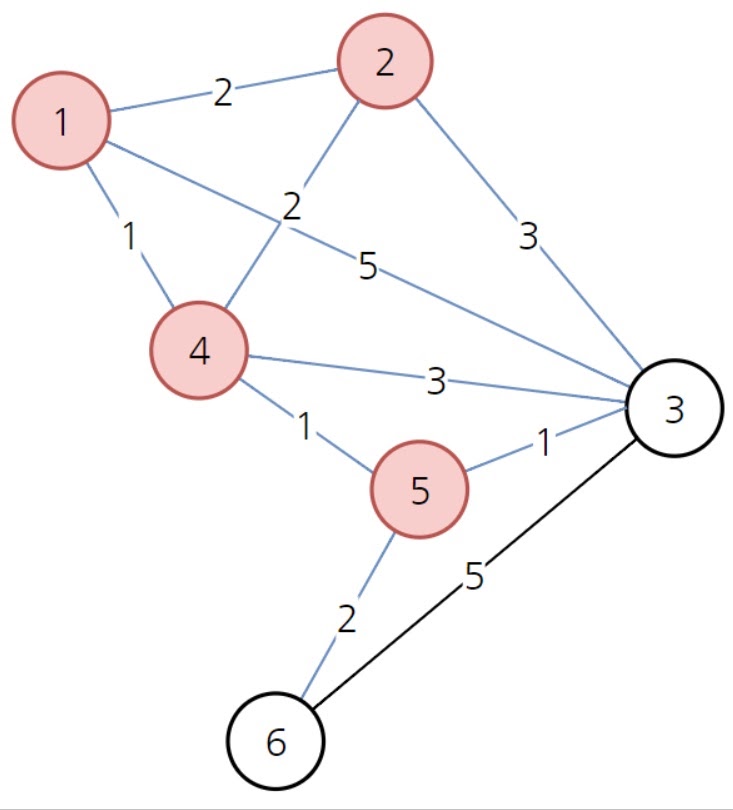
이 경우 1>4>5>3으로 가면 비용이 3으로 기존 4보다 저렴해서 3으로 갱신하고
1>4>5>6으로 가면 비용이 4로 이전 무한대보다 저렴해서 새롭게 갱신한다

이후 3번 노드, 6번 노드를 차례대로 선택해서 최소비용을 갱신하는 과정을 반복하여
모든 노드를 freeze시킴

위 배열이 1번에서 1,2,3,4,5,6번 노드로 가는 각각의 최단 경로 비용을 나타낸다
그러니까 1번에서 6번으로 가는 최단 경로 비용이 4라는 뜻이다
그런데 이렇게 최소 비용인 노드들을 선택해가면서 구현하는 경우 O(N^2)으로 시간복잡도가 커질 수 있음
그래서 단순히 현재 선택된 노드에서 인접 노드를 선택해서 구현하면 O(N*logN)으로 저렴하게 구현할 수도 있음
참고
https://blog.naver.com/ndb796/221234424646
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐...
blog.naver.com
'알고리즘 > 최단거리 알고리즘' 카테고리의 다른 글
| 2차원 배열에도 사용가능한 다익스트라 알고리즘 (0) | 2022.10.07 |
|---|---|
| 특정한 정점을 반드시 거쳐야하는 최단 경로를 구하는 다익스트라 응용 (1) | 2022.10.06 |
| 자다가도 일어나서 바로 구현할 수 있어야하는 최단경로를 찾는 다익스트라 알고리즘 최적화하기 2편 (0) | 2022.10.03 |
| 자다가도 일어나서 바로 구현할 수 있어야하는 최단경로를 찾는 다익스트라 알고리즘 파헤치기 1편 (0) | 2022.10.03 |
| 다익스트라 알고리즘 활용하기 (0) | 2022.01.30 |

