1. 문제
https://programmers.co.kr/learn/courses/30/lessons/49189
코딩테스트 연습 - 가장 먼 노드
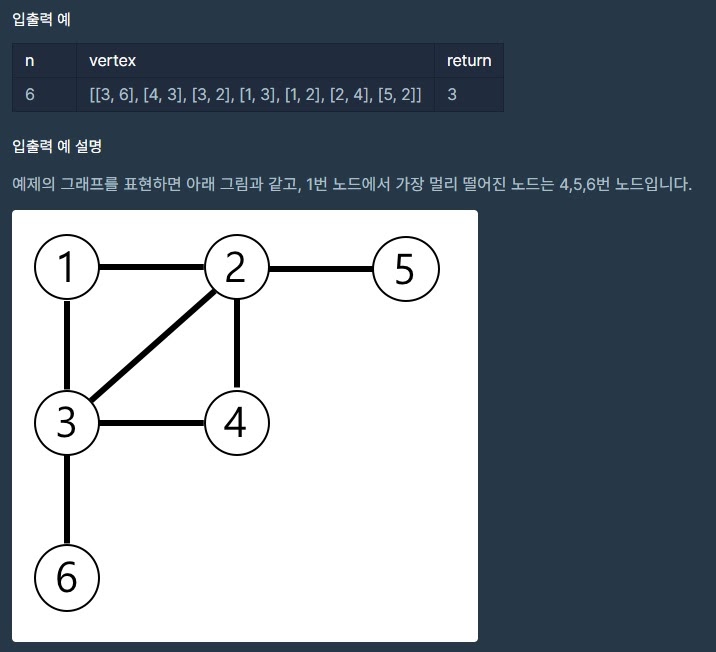
6 [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] 3
programmers.co.kr
n개의 노드가 있는 그래프가 있습니다.
각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 개수를 구하려고 합니다.
가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때
1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return하도록 solution 함수를 작성해주세요
2. 제한사항
노드의 개수 n은 2이상 20000이하입니다.
간선은 양방향이며 총 1개 이상 50000개 이하의 간선이 있습니다.
vertex 배열 각 행 [a,b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
3. 예시
4. 나의 풀이
먼저 필요한 변수 초기화를 수행함
넣고 빼는 작업을 수행해야해서 비용이 O(1)로 저렴한 deque를 이용함
def solution(n,edge):
answer = 0
from collections import deque
graph = {}
costs = {}
freeze_node = set([])
next_node = deque([1])
for i in range(1,n+1):
graph[i] = set()
if i == 1:
costs[i] = 0
else:
costs[i] = 99999
1번 노드부터 시작해야하는데 1번은 수행할 필요가 없으니까 next_node랑 freeze_node에 1을 넣어놓고
cost[1]에 0을 넣고 1이 아닌 다른 부분에는 99999로 무한대를 대신할 값을 넣어놓는다
여기서 중요한 점은 freeze node를 list가 아닌 set으로 구현해놔서 나중에 set으로 바꿀 작업을 미리 해놓는다는 점
마찬가지로 graph[i]를 graph[i]=[]으로 하는게 아니라 graph[i]=set()으로 해서 set으로 미리 구현해놓는다는 점
리스트로 해놓고 반복문에서 set()으로 매번 바꾸는 작업이 시간 효율에 생각보다 결정적이다
for node1, node2 in edge:
graph[node1].add(node2)
graph[node2].add(node1)
edge 정보를 가지고 graph를 구성함
서로 연결된 node라면 edge 안에 들어가있으니까 둘 다 넣어주면 됨
while next_node != deque():
min_node = next_node.popleft()
cost = costs[min_node] + 1
link = graph[min_node]
for node in link:
if costs[node] > cost:
costs[node] = cost
freeze_node.add(min_node)
next_node.extend(deque(graph[min_node] - freeze_node - set(next_node)))
이제 다익스트라 알고리즘에 따라서 프로그래밍을 해본다
먼저 현재 next_node=[1]이 들어가 있는데 여기서 min_node를 먼저 선택할 거임
1번부터 시작할거니까 1번을 선택이 될거
모든 link의 비용은 1이니까 현재 선택된 node인 1번에서 인접한 다른 node로 가는 비용은 costs[min_node]+1로 구할 수 있다
인접한 node 정보는 앞에서 구해놓은 graph에 min_node를 넣으면 인접한 node들을 알 수 있다
-------------------------------------------------------------------------------------------------------------------------------

현재 1번에서 인접한 node는 2번 3번이어서 link=[2,3]이 있을거임
그럼 이제 for문을 돌아서 최소 비용을 갱신하는 작업을 수행할거임
현재 1번에서 1번, 2번,3번,4번,5번,6번으로 가는 비용 리스트
costs = [0,99999,99999,99999,99999,99999] 이렇게 있단 말이지
for node in link:
if costs[node] > cost:
costs[node] = cost
link=[2,3]에서 node=2를 뽑으면 costs[node]=99999이고
1번에서 2번으로 가는 비용은 앞에서 구한 cost[min_node]+1=1로 구했다
그러면 여기서 현재 최소 비용 99999보다 1이 더 저렴하니까 더 저렴하면 1로 갱신을 하는거임
node=3도 마찬가지
freeze_node.add(min_node)
next_node.extend(deque(graph[min_node] - freeze_node - set(next_node)))
1번 node는 탐색했으니까 freeze_node에 1을 추가한다
freeze_node가 set이라서 append가 아니고 add()를 이용함
다음 탐색할 노드를 선택해야하는데 최소 비용 노드가 아니라
그냥 현재 선택된 노드에서 인접한 노드들을 next_node에 추가해줌
최소비용노드들을 선택하면 알고리즘이 느려진다는것을 설명했다
https://deepdata.tistory.com/170
다익스트라(dijkstra) 알고리즘
그래프에서 최단경로를 탐색하는 알고리즘 특정 하나의 node에서 다른 모든 node로 가는 최단 경로를 알려줌 link의 가중치가 음수인 경우는 고려하지 않음 하나의 최단 거리를 그 이전까지 구했던
deepdata.tistory.com
graph[min_node] = set(2,3)
freeze_node = set(1)
set(next_node) = set()
현재 위와 같은 상황에서 차집합을 구해서 중복된 것을 제거하는 식으로 next_node에 추가해줌
이미 탐색한 node를 또 넣어서 탐색하면 시간 비효율적임
이해를 위해 다음에는 next_node = [2,3]이 있어서 다음 min_node=2일 거임
그러면 costs=[0,1,1,99999,99999,99999]인데
cost=costs[min_node]+1은 1번에서 2번 node를 거쳐 다음 2번과 인접한 node들인 3,4,5로 가는데 걸리는 거리인 2가 될거임
link에는 [3,4,5]로 2번과 연결된 거리
for문을 통해서 최소비용을 갱신하는 작업을 수행
link=[3,4,5]에서 node=3이면 costs[3]=1이고 cost=2이니까 최소비용을 갱신하지 않고
node=4이면 costs[4]=99999여서 cost=2니까 최소비용을 2로 갱신해놓음
node=5도 마찬가지니까 최소비용을 2로 갱신해서
costs=[0,1,1,2,2,99999]
다음 next_node를 구해야하는데 2번은 탐색했으니까 freeze_node에 2를 추가하고
graph[min_node]=[3,4,5]로 2번과 인접한 노드들에서
freeze_node=[1,2]로 이미 탐색한 노드들 빼주고
next_node = [3]에서 이미 들어간 3을 또 넣는 행위는 빼준다
그러면 graph[min_node]-freeze_node-next_node=[4,5]이고 next_node에 [4,5]가 들어가 [3,4,5]가 들어가있음
next_node도 set으로 하면 되는거 아니냐? 이럴수 있는데 얘만큼은 deque로 해야 pop할때 O(1)로 시간 줄일수 있음
나머지 node들도 반복을 하면 next_node = []이 되는 순간이 와서 while문을 탈출할 수 있음
-------------------------------------------------------------------------------------------------------------------------------
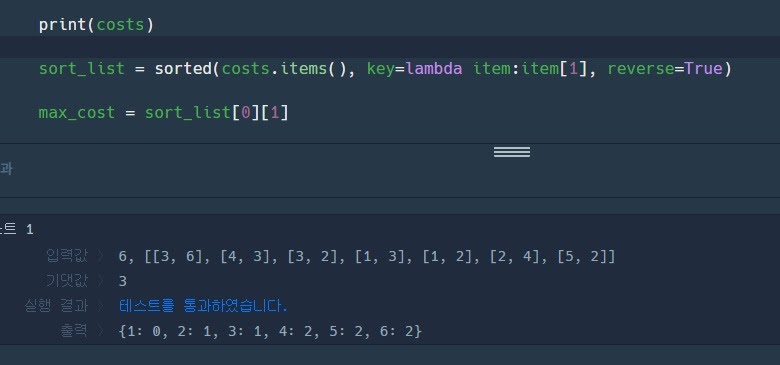
그러면 위와 같이 costs가 구해져있는데
sorted()를 이용해서 cost값을 기준으로 내림차순 정렬한다음에 max cost를 구해 집어넣음
[(6,2), (5,2), …] 이런식으로 되어 있어서 max_cost=2가 들어감
for node, cost in sort_list:
if max_cost == cost:
answer += 1
else:
break
return answer
sort_list에서 cost를 빼서 max_cost와 같으면 answer에 1을 더해주고 다른 순간 break해서 for문 탈출하면 된다
5. 다른 풀이
좋아요 가장 많이 받은 풀이를 보면
def solution(n,edge):
graph = [ [] for _ in range(n+1) ]
distances = [ 0 for _ in range(n) ]
is_visit = [False for _ in range(n)]
queue = [0]
is_visit[0] = True
for (a,b) in edge:
graph[a-1].append(b-1)
graph[b-1].append(a-1)
while queue:
i = queue.pop(0)
for j in graph[i]:
if is_visit[j] == False:
is_visit[j] = True
queue.append(j)
distances[j] = distances[i] + 1
distances.sort(reverse=True)
answer = distances.count(distances[0])
return answer
나랑 풀이가 비슷한것 같기는 하네 근데 시간 훨씬 빠름
먼저 변수 초기화를 수행하고 graph를 구성함
다음 queue가 아마 next_node일거임
queue가 있으면 반복수행을 하고 없으면 while문 탈출하고
----------------------------------------------------------------------------------------------------
queue에서 pop을 해서 next_node인 i를 뽑는다
graph[i]를 하면 i와 인접한 node들이 있는데 for문을 통해서 최소비용을 갱신할거임
is_visit를 이용해서 j를 방문했는지 안했는지 확인을 해서 방문 안했으면 false이고 방문했으면 true일거임
방문 안했으면 방문했다고 true로 바꿔주고 queue에 j를 넣어줌
다음 distance에는 지금까지 최소비용이 있어서 1을 더해서 최소비용을 구해 최소비용을 갱신해줌
근데 이러면 queue에 지금까지 수행했던 node가 중복해서 들어갈건데 is_visit로 걸러질거란 말이지
내가 시간이 더 걸린 이유가 이것저것 쓸데없이 많이해서 그런가보다
마지막에 count를 이용해서 max값이랑 같은 값 개수 세는것도 재밌네
6. 되돌아보기
다익스트라 알고리즘 배웠으니까 이제는 써먹을수 있도록
시간을 줄이는 코딩을 생각하면서 해야함
while문에서 set()으로 바꿀 생각을 하는 것이 아니라
미리 set()으로 구현해놓으면 set()으로 바꾸는 시간을 줄일수 있단 말이지
len이랑 비슷한 원리라고 보면 된다
반복문 같은 것에 들어가기 전에 미리 해놓을 수 있다면 미리 해놓는것 중요하다
'알고리즘 > 최단거리 알고리즘' 카테고리의 다른 글
| 2차원 배열에도 사용가능한 다익스트라 알고리즘 (0) | 2022.10.07 |
|---|---|
| 특정한 정점을 반드시 거쳐야하는 최단 경로를 구하는 다익스트라 응용 (1) | 2022.10.06 |
| 자다가도 일어나서 바로 구현할 수 있어야하는 최단경로를 찾는 다익스트라 알고리즘 최적화하기 2편 (0) | 2022.10.03 |
| 자다가도 일어나서 바로 구현할 수 있어야하는 최단경로를 찾는 다익스트라 알고리즘 파헤치기 1편 (0) | 2022.10.03 |
| 다익스트라(dijkstra) 알고리즘 (0) | 2022.01.29 |

