1. 혼동행렬 완성
ⓐ예측을 기준으로 예측의 P, N을 그대로 쓴 다음에
ⓑ예측 = 실제이면 T를 붙이고 예측 != 실제이면 F를 붙인다

2. 민감도 특이도 정밀도 재현율
실제를 기준으로 묶어서 민감도와 특이도
민감도 = 재현율
대칭방향으로 정밀도

민감도 = $\frac{TP}{TP+FN}$ = 재현율
특이도 = $\frac{TN}{FP+TN}$
정밀도 = $\frac{TP}{TP+FP}$
3. F1 score
재현율과 정밀도의 조화평균
조화평균이란?
역수의 산술평균의 역수
$$F1 = \frac{1}{\frac{\frac{1}{재현율} + \frac{1}{정밀도}}{2}} = \frac{2 \times 재현율 \times 정밀도}{재현율+정밀도}$$
4. TPR, FPR???
1에서 그린 혼동핼렬 표를 보고 TPR을 구하고 싶다면??
TP를 찾아서 실제를 기준으로 묶어서 비율 그대로
마찬가지로 TNR을 구하고 싶다면??
TN을 찾아서 실제를 기준으로 묶어서 비율 그대로

그리고 나서 그대로 해석해
TPR은 참금정률
실제 참인 데이터 중에서 모델이 긍정이라고 예측한 비율
TNR은 참부정률
실제로는 거짓인 데이터 중에서 모델이 부정이라고 예측한 비율
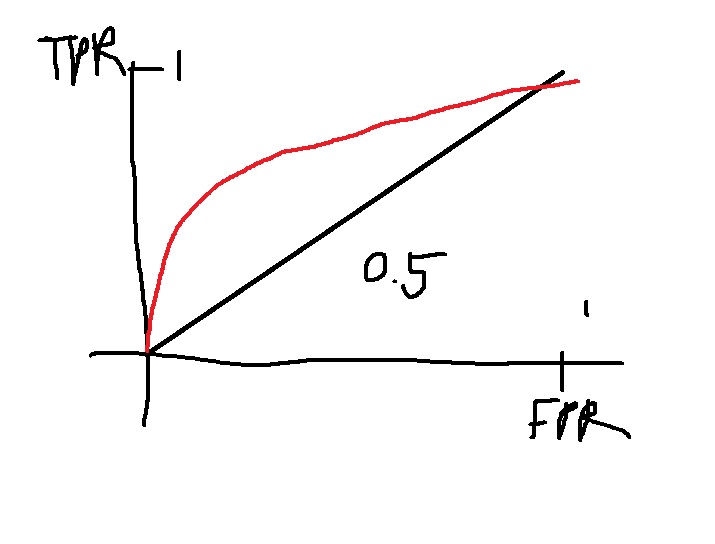
5. ROC curve
민감도와 특이도를 고려하여 최적의 모델을 찾기 위해 고안된 곡석인데
Y축인 세로축에 민감도를 세워서 0에서 1로 증가하면
X축인 가로축에 특이도를 세우면 0에서 1로 증가하는 것이 아니라 민감도와는 반대로 1에서 0으로 감소한다
근데 이제 이게 보기 안좋으니까 X축에는 1-특이도를 세워서 0에서 1로 똑같이 증가하도록 만드는 것이다.
아무튼 X축을 FPR, Y축을 TPR
그러면 FPR과 TPR이 뭔지 아니까 1-특이도와 민감도라는거 안외우고도 파악 가능
ROC곡선의 아래 면적의 최솟값은 0이 아니라 0.5이고 최댓값은 1이다.
6. 카파(Kappa)
두 모델이 데이터를 측정할 때 범주에 대한 일치도를 측정하는 상관계수
두 모델이 우연히 일치하도록 측정했는지, 무관하게 정말로 일치하게 측정했는지 판단하고자 함
전문가 한 명이 시스템 성능 평가를 위해 만들어 놓은 Gold-standard(정답)이 신뢰성이 없다면 이 정답을 사용하여 평가한 시스템 결과는 믿음직스럽지 못할 것
만약 다른 전문가 한명이 시스템 성능 평가를 위해 만든 정답과 기존의 전문가의 평가가 유사하다면, 즉 카파 상관계수가 높다면 이 시스템 평가 결과는 믿을만 하게 되는 것
모델1, 모델2를 모델, 실제 데이터로 바꿔서 생각해본다면..?
모델의 예측 결과와 실제 데이터가 우연히 일치할 확률을 제외한 뒤에 평가하는 지표
0에서 1
0에 가까울수록 우연히 일치한 것으로 신뢰하기 힘들다
1에 가까울수록 모델의 예측 결과와 실제 데이터가 정말로 일치한다는 의미

P(a)는 정확도
P(e)는 모델의 예측과 실제 데이터가 우연히 일치할 확률
7. 참고
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=y4769&logNo=220680837692
[SPSS 24] Cohen's Kappa 계수
SPSS 24 버전이 출시된 기념으로 오랜만에 통계 포스팅을 준비해보았다. 요즘은 인터넷에 방대한 자료...
blog.naver.com
https://blog.daum.net/jungjin1980/462
kappa 상관계수
출처 : http://unlimitedpower.tistory.com/entry/IR-Cohens-Kappa-Coefficient%EC%B9%B4%ED%8C%8C-%EC%83%81%EA%B4%80%EA%B3%84%EC%88%98 Cohen's Kappa Coefficient(카파 상관계수)는 카테고리 정보에 대한 2명..
blog.daum.net
https://yogyui.tistory.com/entry/Confusion-Matrix-%ED%98%BC%EB%8F%99%ED%96%89%EB%A0%AC
Confusion Matrix (혼동행렬)
지난주 토요일(4/17) 빅데이터분석기사 필기시험을 치렀다 데이터분석전문가(ADP)를 딴지 얼마 안돼서 그런지 체감 난이도는 그저 그런 수준? (어차피 출제기관은 한국데이터산업진흥원으로 동일
yogyui.tistory.com
'다시보는 통계학' 카테고리의 다른 글
| 조건부독립의 성질 (0) | 2022.01.30 |
|---|---|
| 회귀분석에서 회귀계수는 유의하지만 절편이 유의하지 않다면..? (0) | 2022.01.30 |
| 무의식적인 통계학자의 법칙(Law Of The Unconscious Statistician) (0) | 2021.12.30 |
| 몬테카를로(Monte-Carlo) 시뮬레이션에 대한 이론적인 설명 (0) | 2021.12.21 |
| 경험분포함수(empirical distribution function) (0) | 2021.12.08 |

