연속형확률변수 $X$의 확률밀도함수가 $f(x)$일 때 연속형 확률변수 $X$의 기댓값은
\[E(X)=\int_{}^{}xf(x)dx\]
이산형 확률변수 $X$의 확률질량함수가 $P(X=x)$일 때 기댓값은
\[E(X)=\sum_{}^{}xP(X=x)\]
확률변수 $X$의 함수 $g(X)$도 하나의 확률변수이고
그러므로 기댓값이 존재하는데 다음과 같은 식이 성립한다
$X$가 연속형이면
\[E(g(X))=\int_{}^{}g(x)f(x)dx\]
$X$가 이산형이면
\[E(g(X))=\sum_{}^{}g(x)P(X=x)\]
이것을 무의식적인 통계학자의 법칙(Law Of The Unconscious Statistician, LOTUS)이라고 부른다.
$X$의 기댓값을 구할 때 $X$의 확률함수를 이용해서 구했는데,
$X$의 함수인 $g(X)$도 하나의 확률변수로 기댓값을 구할 때 $g(X)$의 확률함수를 알아야 할 것 같지만
$X$의 확률함수만 알아도 기댓값 식에서 무의식적으로 $x$대신에 $g(x)$를 써서 구할 수 있다는 점에서 의미가 있다.
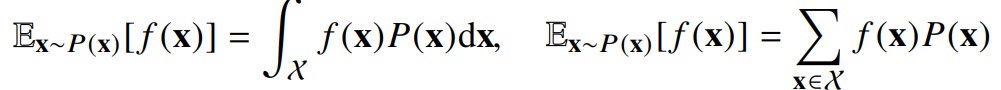
728x90
'다시보는 통계학' 카테고리의 다른 글
| 회귀분석에서 회귀계수는 유의하지만 절편이 유의하지 않다면..? (0) | 2022.01.30 |
|---|---|
| 데이터 시험 단골손님인 혼동행렬(confusion matrix) 민감도 특이도 완전정복 (0) | 2022.01.29 |
| 몬테카를로(Monte-Carlo) 시뮬레이션에 대한 이론적인 설명 (0) | 2021.12.21 |
| 경험분포함수(empirical distribution function) (0) | 2021.12.08 |
| 누적분포함수와 분위수(quantile)의 관계 (0) | 2021.12.08 |

