1. 카탈란 수
n = 0,1,2,3,...에 대하여 다음과 같은 수열
1,1,2,5,14,42,132,429,1430,4862,16796,58786,....
0이상의 n에 대하여 카탈란 수 $C_{n}$는 다음과 같은 재귀적 관계를 만족한다.
$$C_{0} = 1, C_{n} = \sum_{i = 1}^{n} C_{i-1}C_{n-i}$$
이는 다음과 같이 정리할 수 있고
$$C_{0} = 1, C_{n} = \frac{2(2n-1)}{n+1}C_{n-1}$$
점화식을 풀면 다음과 같이 일반항을 도출할 수 있다.
$$C_{n} = \frac{1}{n+1} * \binom{2n}{n}$$
2. 응용
1) Dyck word
n개의 X와 n개의 Y로 이루어진 문자열 중 처음부터 하나씩 셌을때 Y의 개수가 X의 개수보다 많아지지 않는 것의 개수는?
X가 항상 Y보다 많거나 같다.
예를 들어 XY,XXYY,XYXY,XXXYYY,XYXXYY,XYXYXY,XXYYXY,XXYXYY,...
길이가 2n인 dyck word를 생각해보자. 이를 만족하는 단어의 개수를 C(n)이라고 한다.
문자열의 첫번째 문자는 항상 X이다.
이 X와 처음으로 짝을 이루는 Y를 찾으면 그것을 기준으로 문자열을 두 부분으로 나눌 수 있다.
XYXXYY는 XY와 XXYY
첫번째 부분의 단어에서 X와 Y의 개수가 같아지는 최소 인덱스를 j라고 하면 j = 2k+2, k >= 0이다.
왜냐하면 첫 글자가 반드시 X이고, X와 Y의 개수가 서로 같으므로 길이가 2 이상인 짝수이기 때문이다.
첫 단어는 이때 X A Y로 분해할 수 있다.
A는 두번째 문자부터 j-1번째 문자까지의 부분 문자열이고 길이가 2k이면서 Dyck word이다.
왜냐하면 XAY가 Dyck Word이기 때문이다.
두번째 부분을 B라고 하면 길이가 2n에서 2k+2를 제외한 2n-2k-2인 단어이고 이 역시 Dyck Word여야 한다.
왜냐하면 XAYB가 Dyck Word이기 때문이다.
이때 모든 가능한 k <= n-1에 대하여 A,B를 결정하는 방법의 수는 A는 길이가 2k인 Dyck word의 개수 C(k)이고
B는 길이가 2(n-k-1)인 Dyck word의 개수이므로 C(n-k-1)이다.
따라서, 길이가 2n인 Dyck word의 개수는 $C(n) = \sum_{k = 0}^{n-1} C(k)C(n-k-1)$
$C_{n}$은 길이가 2n인 Dyck word의 개수를 나타낸다.
2) y=x를 넘어가지 않는 경로
2차원 배열 위 (0,0)에서 (n,n)으로 이동하는 경로 중에서 오른쪽 또는 위로만 이동하는 경로를 세는데
y = x를 넘어가지 않는 경로의 수는 몇가지인가?

이는 잘 생각해보면 Dyck Word의 개수를 세는 것과 동치이다.
X를 오른쪽으로 이동, Y를 위로 이동이라고 하면, X의 개수가 Y의 개수 이상이어야하므로,
X,Y로 이루어진 Dyck Word의 개수와 같다.
따라서 이 역시 카탈란 수 C(n)과 같다.
3) 길이가 2n인 올바른 괄호 문자열의 개수
올바른 괄호 문자열은 여는 괄호와 닫는 괄호가 맞아떨어지는 문자열이다.
예를 들어 (), (()), ()() 등등
X가 (
Y가 )으로 생각하면 이 역시 X,Y로 이루어진 Dyck Word의 개수와 같다.
4) 이항 연산의 방법의 수
n+1개의 항에 이항연산의 순서를 적용하는 방법의 수는?
5개의 항의 곱 abcde에 괄호로 이항연산의 순서를 표시하면
(((ab)(cd))e)
(a(b(c(de))))
((a(b(cd)))e)
....
이 역시 n+1개의 항이 존재하면 길이가 2n인 올바른 괄호 문자열의 개수와 동일한 문제이므로 카탈란 수로 구해진다
5) n+2각형을 n개의 삼각형으로 나누는 방법의 수
n+2각형을 교차하지 않는 선분으로 꼭짓점을 연결해서 삼각형으로 나눌 수 있는데, 이 때 n개의 삼각형이 형성된다.
이를 만드는 방법의 수는?
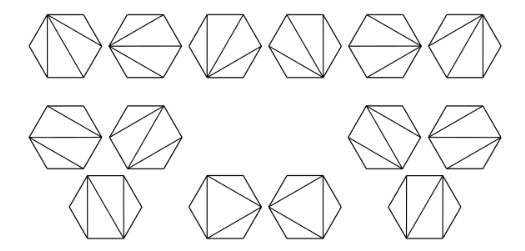
다각형의 각 변을 a,b,c,d,e,f라고 표시하고 삼각분할을 하면, 분할한 변에 따라 묶어서 (cd), b(cd)...
등등으로 묶여서 이항연산의 괄호치기 문제랑 동일한 문제가 된다

6) n+1개의 리프노드가 있는 이진 트리의 수
이항 연산의 반복은 이진트리로 표현할 수 있다
리프 노드를 각각 A,B,C,D,...로 표시하고 이진 트리에서 각 형제노드끼리 묶어서 표시하면
아래 그림에서 ((AB)(C)) 이런 식으로
그래서 리프 노드가 n개인 이진트리의 개수는 이항 연산의 개수와 같게 된다.

7) 높이가 n인 계단 모양을 n개의 직사각형으로 완전히 채울 수 있는 경우의 수

노드가 n개인 이진트리로 바꿀 수 있다고 한다
근데 이건 느낌이 잘 안옴
예를 들어 이런식인것 같은데


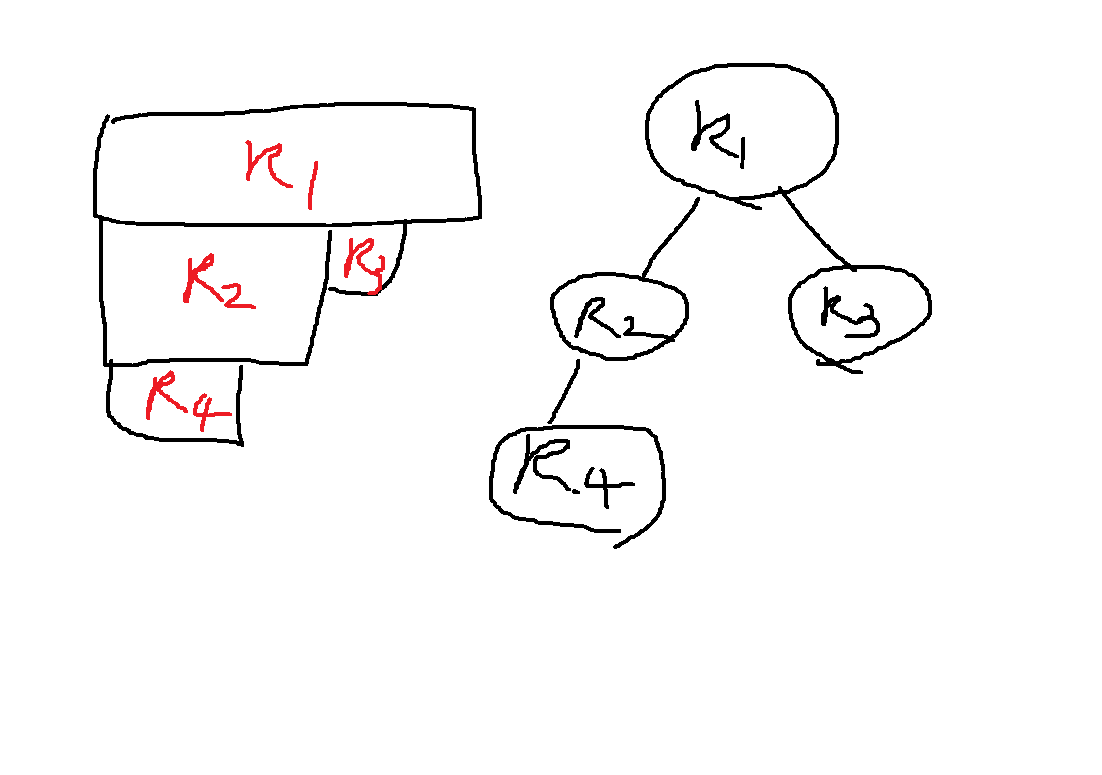
얘는 첫번째랑 똑같은건가?
근데 자식이 왼쪽에 있고 오른쪽에 있고에 따라 사각형 타일링 모양이 다른건지
정확한 설명이 없어서 잘 모르겠는데
아무튼 이진트리랑 사각형 타일링이랑 대응시킬수는 있는듯?

8) 원 위의 2n개의 점에서 서로 다른 두 점을 선택하여 선분을 그을때 교차하지 않도록 긋는 방법의 수
원 위의 각 점이 P1,P2,P3,...,P2n이라고 하자.
어떤 다른 점 P(2k+2)와 P1을 그어 선분을 그으면 이 선분은 원을 두 부분으로 분할한다.
그러면 P1에서 P(2k+2)까지 있는 점들의 개수는 2k+2개이고 P1,P(2k+2)는 연결되어있으므로 2k개의 점으로 선분을 긋는 문제이다.
반대편은 P(2k+2)와 P1을 제외한 나머지 점들의 집합으로 2n - (2k+2) = 2(n-k-1)개의 점으로 선분을 긋는 문제가 된다.
2n개의 점으로 교차하지 않게 선분을 긋는 방법의 수를 T(n)이라고 한다면,
따라서 두 부분은 k = 0,1,2,..,n-1에 대하여 $\sum_{k=0}^{n-1} T(k) * T(n-k-1)$가지로 이는 카탈란 수와 동일하다.
---------------------------------------------------------------------------
이외에도 엄청 많다고함
-------------------------------------------------------------------------
3. 문제
원탁 위에 짝수 n명이 앉아서 악수하는데, 서로 팔이 교차하지 않도록 악수할 경우의 수를 구하는 문제
위의 8)번과 완전히 동일한 문제이다
팩토리얼을 구해서 카탈란 수를 직접 구하거나
n = int(input())
f = [0]*(n+1)
f[0] = 1
for i in range(1,n+1):
f[i] = f[i-1] * i
mod = 987654321
print(f[n]//(f[n//2]*f[n//2]*(n//2+1)) % mod)
카탈란 수 점화식을 이용하는 방법도 있다
n = int(input())//2
c = [0]*(n+1)
c[0] = 1
mod = 987654321
for i in range(1,n+1):
for k in range(i):
c[i] += c[k]*c[i-1-k]
c[i] %= mod
print(c[n] % mod)
'조합론' 카테고리의 다른 글
| 여사건을 이용한 경우의 수1 - 특정 수를 포함하는 부분집합 구하는 법 (0) | 2024.08.23 |
|---|---|
| m면체 주사위 n개를 굴려서 나올 수 있는 경우의 수를 구하는 방법 (0) | 2024.08.17 |
| 경기장 일렬 좌석에 앉을 때 사람을 지나치지 않고 전부 앉는 방법의 수 (0) | 2024.07.26 |
| 다항식의 곱으로 구하는 복수순열1 - 주어진 개수의 알파벳들만으로 만들 수 있는 문자열의 개수 (0) | 2024.06.18 |
| 원형테이블에 앉은 n명의 사람 중 서로 인접하지 않은 k명의 사람을 뽑는 방법 (0) | 2024.06.07 |

