sound source localization의 unsupervised learning에서 설명한 방식이 사실 triplet loss를 이용한 것이다.
metric learning의 일종
기준이 되는 image data에 대응하는 audio data를 positive data라고 하고 (fv,fs+)라고 표시하자.
반대로 image data에 대응하지 않는 데이터는 negative data라고 하고 (fv,fs-)라고 표시한다.
위에서 fv는 지금 동일한 기준 데이터임
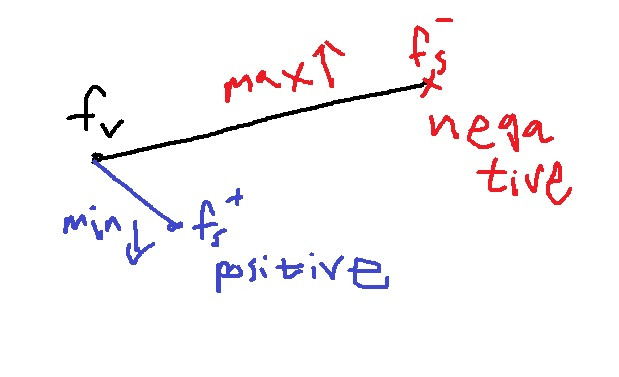
직관적으로 fv와 fs+ 는 서로 대응하는 관계니까 거리가 가까워야하고 fv와 fs-는 서로 대응하지 않으니까 거리가 멀어야한다.
공간상에 positive data는 가깝게 negative data는 멀게 분리하여 배치하는 것이 triplet loss의 목적
triplet loss는 fv와 fs+사이의 거리는 최대로 만들고 fv와 fs-사이의 거리는 최소로 만들도록 설계한다.
보통 거리는 L2 norm으로 구하여 $ |f_{v} - f_{s}^{+}|_{2} + \alpha < |f_{v} - f_{s}^{-}|_{2}$이 성립한다.
모든 데이터에 대하여 positive distance와 margin $\alpha$의 합이 negative distance보다 작다.
따라서 수학적으로 triplet loss function은 $$ \sum_{}^{} |f_{v} - f_{s}^{+}|_{2} + \alpha - |f_{v} - f_{s}^{-}|_{2}$$
이라고 정의하면 loss가 최소인 것은 positive distance가 최소이고 negative distance가 최대인 경우이다.
margin $\alpha$은 보통 1을 쓰는데 triplet loss를 사용한 논문마다 나름대로 사용하는 방법이 다 다르다.
심지어 최초로 사용한 논문에서는 margin이라는 말을 쓰지도 않았다… 근데 거기서는 1을 쓴 것 같긴함

아무튼 결론적으로 중요한 점은 positive distance는 최소로 만들고 negative distance는 최대로 만들겠다는 원리가 triplet loss의 핵심 원리다.
'딥러닝 > Computer Vision' 카테고리의 다른 글
| 컴퓨터 비전에서 사용하는 기본적인 data augmentation 2 (0) | 2024.09.23 |
|---|---|
| visual and audio cross modal reasoning2 - speech separation, lip move generation (0) | 2024.09.10 |
| visual and audio cross modal reasoning1 - sound source localization (0) | 2024.09.09 |
| 3D task를 위한 dataset과 3d task (0) | 2024.07.08 |
| 3D 이해하기2 - 3D를 표현하는 방법 (0) | 2024.05.08 |

