1. matrix factorization
사용자 * 아이템으로 구성된 하나의 행렬을 2개의 행렬로 분해하는 방법
사용자와 아이템이 각각 무엇인지는 모르겠지만 k개의 잠재요인(latent factor)으로 설명할 수 있다고 생각하고,
(사용자 * 잠재요인) * (잠재요인 * 아이템)의 두 행렬의 곱으로 나타낼 수 있다는 것이다.

행렬 R은 M명의 사용자가 N개의 아이템에 대해 평가한 점수가 있는 행렬
M명의 사용자는 모든 아이템에 대해 평가하지는 않는다.
내가 소유한 아이템, 경험해본 아이템에 대해서는 평가할 수 있어도(혹은 평가하지 않고)
경험해보지 않은 아이템에 평가하지는 않는다(거짓으로 할수도 있겠지만..)
그래서 R은 대부분의 아이템이 NULL인 sparse matrix이다.
이러한 행렬 R을 사용자 행렬 P와 아이템 행렬 Q로 나누어 분석하는 것이 matrix factorization이다.
K개의 잠재요인(latent factor)에 대하여 사용자 행렬 P는 M*K이고 아이템 행렬 Q는 N*K이다.
행렬 P와 Q^T의 곱이 원본 행렬 R에 최대한 가깝게 되는 그러한 행렬 P와 Q를 찾아
사용자가 평가하지 않은 아이템에 대한 평가점수를 추정할 수 있게 된다.

https://velog.io/@vvakki_/Matrix-Factorization-2
Matrix Factorization (2)
[Post No.003] Matrix Factorization의 기본 개념
velog.io
사용자1의 feature1,feature2,..., featurek에 대한 벡터와
아이템1,아이템2,...,아이템n의 feature1,feature2,...,featurek에 대한 벡터의 내적으로
행렬 R의 첫행이 결정되는데 이것이 무엇을 의미하는가?

두 벡터의 내적은 두 벡터가 얼마나 비슷한지를 나타내는 정도로 볼 수 있으므로,
내적값이 높다는 것은 사용자가 해당 아이템과 특징이 비슷하다는 것으로, 내적이 높은 아이템을 추천해주면 된다는 뜻이 된다.
따라서 좋은 P와 Q를 어떻게든 찾으면 두 행렬의 곱으로 사용자가 아이템에 대한 평가 점수를 추정할 수 있고
그러한 추정된 점수를 바탕으로 평가하지 않은 아이템 중 해당 사용자에게 가장 좋을 것 같은 아이템을 추천해주면 좋을 것이다.
예를 들어 4명의 사용자 가연, 수연, 서현, 수경에게 기생충, 겨울왕국, 부산행, 백두산 4개의 영화를 추천해주고자 한다.
만약 사용자와 영화 사이 2개의 공통 요인이 (액션 ~ 드라마), (판타지 ~ 사실주의)로 설명할 수 있다고 하자.
| 액션 - 드라마(-1 ~ 1) | 판타지 - 사실주의(-1 ~ 1) | |
| 가연 | -0.43 | 0.21 |
| 수연 | 0.31 | 0.92 |
| 서현 | 0.69 | -0.03 |
| 수경 | 0.46 | -0.30 |
액션 - 드라마가 -1에 가까울수록 액션을 좋아하고 1에 가까울수록 드라마를 좋아한다고 생각하면 좋다.
판타지 - 사실주의도 마찬가지다.
그러면 사용자가 영화를 볼때 어떤 성향을 가지고 영화를 고르는지 생각할 수 있다.
예를 들어 수연의 판타지 - 사실주의 점수는 0.92이므로 사실주의 영화를 고르는 경향이 강하다고 생각할 수 있다.
| 액션 - 드라마(-1 ~ 1) | 판타지 - 사실주의(-1 ~ 1) | |
| 기생충 | 0.31 | 0.60 |
| 겨울왕국 | 0.61 | -0.82 |
| 부산행 | -0.38 | -0.61 |
| 백두산 | -0.79 | 0.08 |
그러면 각각의 영화도 비슷하게 어떤 성향이 강한지 설명할 수 있다.
예를 들어 겨울왕국은 판타지 - 사실주의가 -0.82이므로 판타지 성향이 강하다고 생각할 수 있다.
이제 두 행렬의 곱 PQ^T는 사용자와 영화 벡터의 내적을 행렬로 나타내므로,
사용자 벡터와 영화 벡터의 내적을 통해 사용자와 영화가 얼마나 서로 비슷한지를 나타내는 점수라고 생각할 수 있다.
| 기생충 | 겨울왕국 | 부산행 | 백두산 | |
| 가연 | -0.0073 | -0.4345 | 0.0353 | 0.3565 |
| 수연 | 0.6481 | -0.5653 | -0.6790 | -0.1713 |
| 서현 | 0.1959 | 0.4455 | -0.2439 | -0.5475 |
| 수경 | -0.0374 | 0.5266 | 0.0082 | -0.3874 |
빨간색으로 된 부분이 각 사용자가 영화에 줄 예상 평점중 가장 높은 부분으로, 각 사용자가 해당 영화와 가장 잘 맞을 것임을 보여주는 것이다.
따라서 그러한 영화를 추천해주는 것이 가장 좋다.
하지만 원래 우리가 아는 정보는 각 사용자가 영화에 대해 어떤 평점을 주었는지 기록한 행렬 R이다.
| 기생충 | 겨울왕국 | 부산행 | 백두산 | |
| 가연 | 1 | 1 | ||
| 수연 | 1 | |||
| 서현 | 1 | 1 | ||
| 수경 | 1 |
즉 위와 같이 자기가 본 영화에 대해서만 기록해 둔 행렬만 주어지고, 이로부터 행렬 P,Q를 찾은 다음
P,Q의 곱으로 기록되지 않은 부분의 점수를 추정하여, 보지 않은 영화 중 좋아할 것 같은 영화를 추천해주는 것이
추천시스템의 본질이다.
즉 R로부터 좋은 P,Q를 어떻게 찾는 것이 좋은가가 문제가 된다.
2. singular value decomposition
https://deepdata.tistory.com/1249
여러가지 matrix decomposition(eigenvalue, singular value, CP, Tucker, non-negative,...)
1. 용어 matrix나 tensor는 데이터 모델링을 위한 도구이다. matrix가 2차원에 숫자를 나열해놓는 것이라면 tensor는 3차원에 숫자를 나열해놓는 데이터 모델링 도구 n*n square matrix에 대한 decompos
deepdata.tistory.com
행렬 R의 singular value decomposition으로 U, $\sum_{}^{}$, V로 분해하여
$U \sum_{}^{} = P$, V = Q로 둔다면 적절한 P,Q로 생각할 수 있을 것 같다.

singular value decomposition에서 $\sum_{}^{}$의 차원이 m*n이며
main diagonal에 singular value가 큰 값으로 내림차순으로 구해져있다
각각의 singular value는 latent factor의 중요도라고 볼 수 있고
여기서 모든 singular value를 사용할 수도 있겠지만, 여러가지 이유로 핵심적인 k개의 singular value만 사용하여 원래 행렬에 근사시킬 수도 있다.

그래서 latent factor의 개수로 가정하는, 이 선택하는 K값은 hyperparameter이다.
3. 구현 예시
데이콘의 웹 기사 추천 AI 경진대회에서 3등을 수상했습니다.
https://dacon.io/competitions/official/236290/overview/description
웹 기사 추천 AI 경진대회 - DACON
분석시각화 대회 코드 공유 게시물은 내용 확인 후 좋아요(투표) 가능합니다.
dacon.io
각 유저가 조회한 기사 로그 기록을 바탕으로, 각 유저에게 5개의 기사를 추천하는 문제
이미 조회한 기사도 추천해줄 수 있다.

각 유저가 조회한 기사를 바탕으로 기사를 추천해주는 문제이므로, 사용자 - 기사 행렬, 위에서 보인 행렬 R을 만드는 코드
import pandas as pd
import numpy as np
from scipy.sparse import csr_matrix
from scipy.sparse.linalg import svds
# 데이터 로드
view_log_train = pd.read_csv('/content/drive/MyDrive/dacon/web/view_log.csv')
article_info = pd.read_csv('/content/drive/MyDrive/dacon/web/article_info.csv')
submission = pd.read_csv('/content/drive/MyDrive/dacon/web/sample_submission.csv')
# 사용자-기사 행렬 생성
user_article_matrix = view_log_train.groupby(['userID', 'articleID']).size().unstack(fill_value=0.0)
조회하지 않은 기사는 0으로 채운다.
기사 수는 약 3000개인데 각 유저는 1개~37개정도의 기사를 조회하므로, 대부분의 원소가 0인 sparse matrix
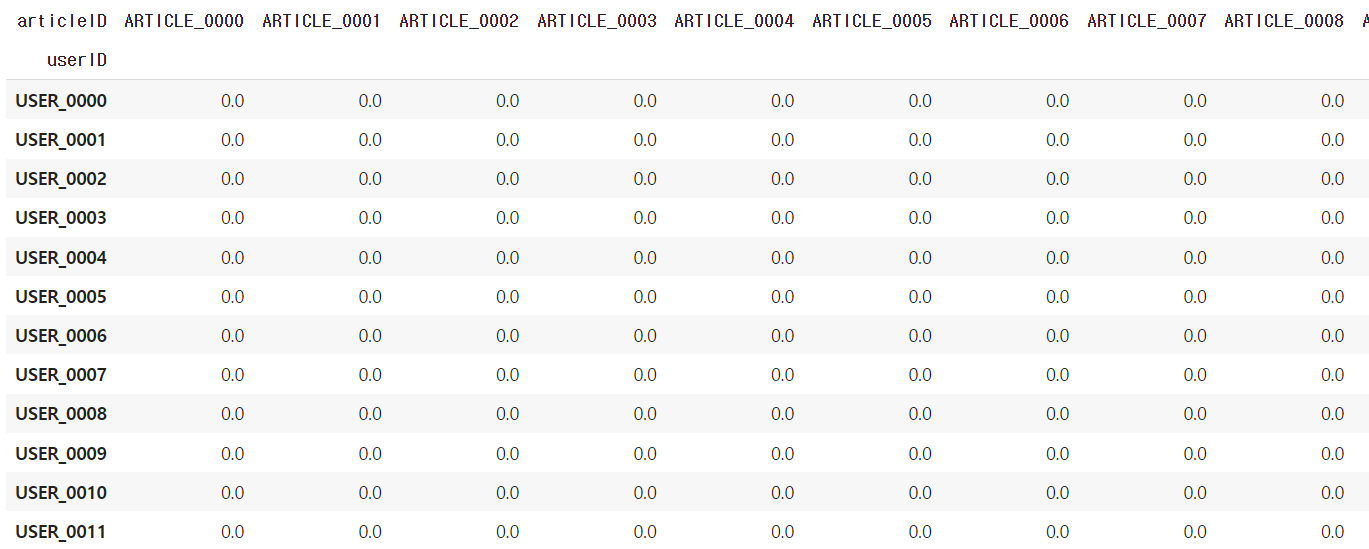
csr_matrix()로 sparse matrix 데이터 타입으로 바꿔줌
number_of_factors_mf는 K값으로 이 값이 클수록 성능이 좋아지는데, 무작정 클수록 좋아지는건 아님
# 1. matrix factorization
users_article_sparse_matrix = csr_matrix(user_article_matrix)
NUMBER_OF_FACTORS_MF = 600 #600 근방에서 성능이 가장 좋았음
U, sigma, Vt = svds(users_article_sparse_matrix, k = NUMBER_OF_FACTORS_MF) #singular value decomposition
sigma = np.diag(sigma)
all_user_predicted = np.dot(np.dot(U, sigma), Vt) #prediction
all_user_predicted_norm = (all_user_predicted - all_user_predicted.min()) / (all_user_predicted.max() - all_user_predicted.min())
cf_preds_df = pd.DataFrame(all_user_predicted_norm, columns = user_article_matrix.columns, index = user_article_matrix.index).transpose()
svds는 singular value decomposition을 수행해줌
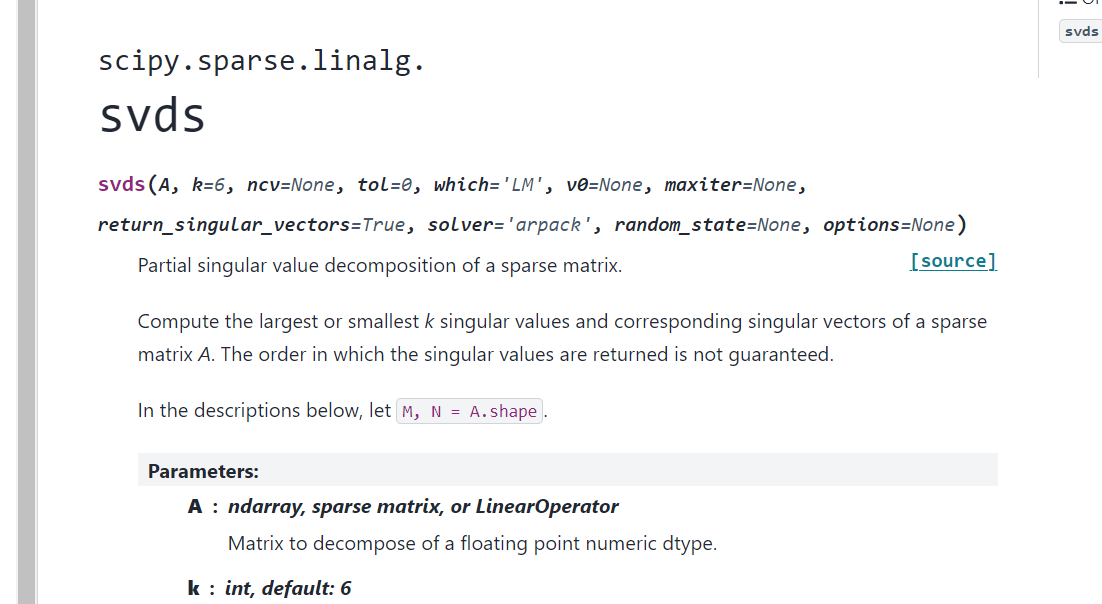
sigma가 singular value들로만 나오는데
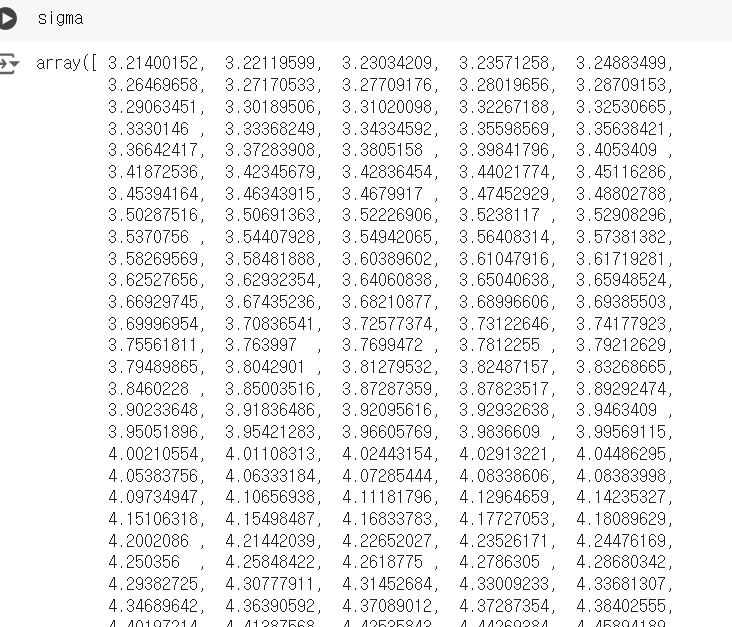
np.diag()로 씌워서 대각행렬로 만들어주고
all_user_predicted = np.dot(np.dot(U, sigma), Vt) 으로 $R \approx PQ^{T}$으로 근사시키던거
그리고 값이 많이 차이날 수 있어서 normalize해줌

그리고 마지막에 user별로 각 기사에 대한 추천 점수가 구해짐
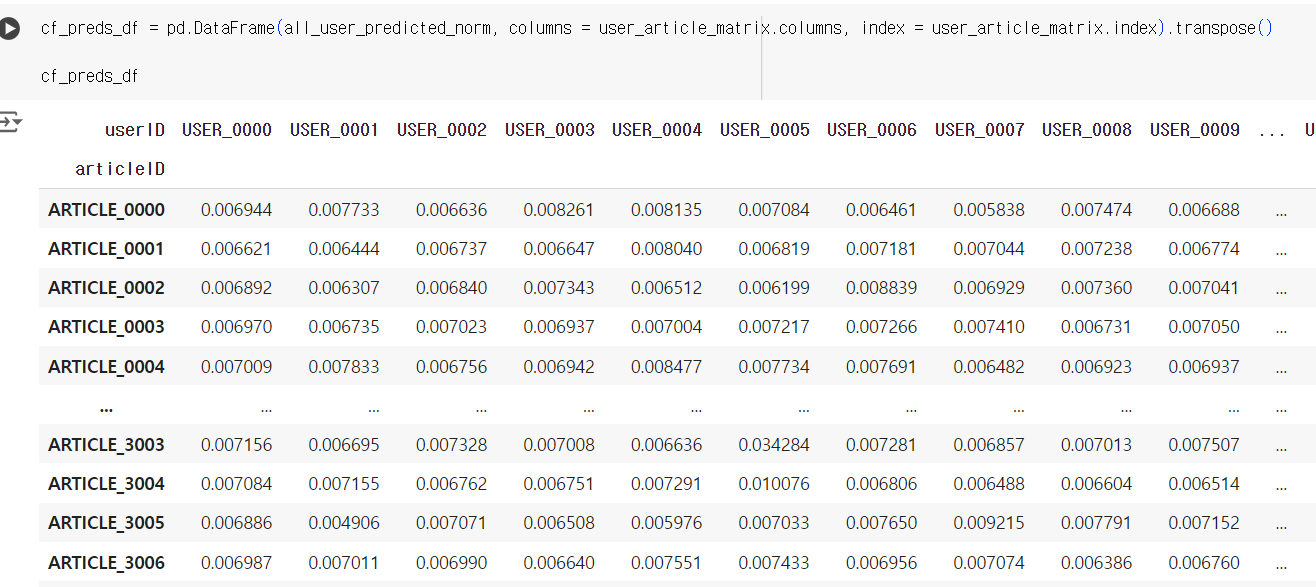
그러면 각 유저별로 가장 점수가 높은 5개의 기사를 추천해주는게 적절한 방법중 하나이다.
'딥러닝 > recommendation system' 카테고리의 다른 글
| 시간에 따른 편향을 고려한 latent factor model (0) | 2024.07.19 |
|---|---|
| 사용자와 상품의 편향을 고려한 latent factor model (0) | 2024.07.17 |
| latent factor model for recommendation system (0) | 2024.07.16 |
| 추천시스템 평가 방법 (0) | 2024.07.05 |
| 추천시스템 기본이론2 -collaborative filtering- (0) | 2022.11.10 |

