1. motivation
UV decomposition이라고도 부른다. (SVD라고도 부르나 수학에서 말하는 SVD랑은 조금 차이가 있음)
사용자와 상품그래프에서 사용자와 상품 node를 embedding vector로 잘 표현하는 것이 핵심이다.
2. example of embedding
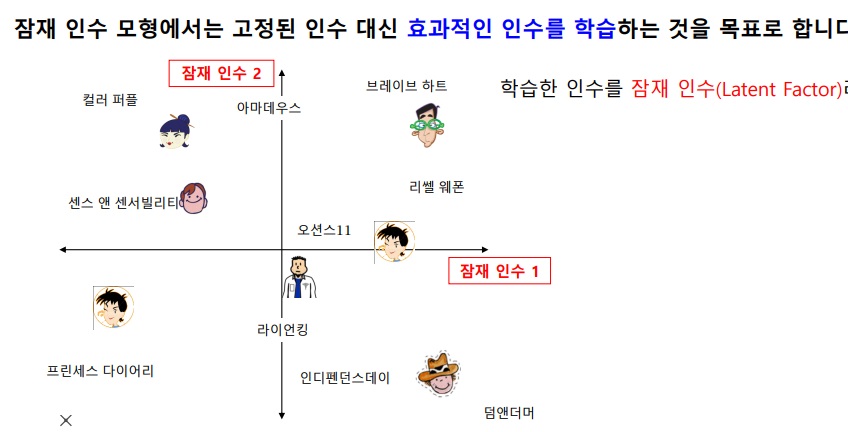
사용자와 영화의 정보를 바탕으로 embedding한 예시

빨간색 네모부분 사람은 영화 브레이브하트와 리쏄 웨폰과 가까워서 이 영화를 추천하겠다
그러나 latent factor model의 핵심은
위와 같은 고정된 인수(액션, 로맨스 영화 등등)를 가지는 차원이 아닌
사용자와 상품의 정보를 효과적으로 학습하여 가장 추천을 잘 해줄법한 latent factor를 찾아내 그곳으로 embedding하겠다는 것이다.
3. 어떻게 embedding을 할까?
사용자와 상품의 정보를 가진 embedding의 내적이 실제 상품의 평점과 가장 가깝게 만든다

내적한 값이 평점과 유사하게 되는 사용자와 상품의 두 embedding vector를 찾겠다
상품,사용자 embedding을 합쳐서 행렬로 확장할 수 있다.
평점 행렬을 아래와 같이 상품행렬(U)과 사용자행렬(V) <자료에는 Q,P로 되어있긴 한데..)로 분해할 수 있다고 해서 UV분해라는 이름이 붙었다.

상품과 사용자 행렬의 곱으로 실제 평점 행렬을 분해하겠다는 생각에 UV분해라는 이름이 붙었다.
실제 평점 행렬과 가장 가까운 UV에 대해 U,V를 찾고 싶은 것
4. loss function
상품과 사용자 embedding의 내적과 실제 평점의 차이를 최소로 만드는 것이 목표

그러나 위와 같은 loss function을 사용하면 과적합 가능성이 있다.
loss를 잘 줄이지만 훈련데이터의 noise까지 학습하여 실제 추천을 해줘야하는 상황에서 제대로 추천을 못해준다
5. Regularization
위에서 구한 오차(평점과 사용자 상품 embedding의 내적의 차이)를 최소화하면서 모형의 복잡도까지 최소화하겠다.

embedding vector의 크기?가 너무 크면 훈련데이터의 noise도 배우니까 가장 중요한 것만 배우도록 복잡도를 낮추겠다는 것
hyperparameter인 $\lambda_{1}, \lambda_{2}$를 크게하면 모형 복잡도를 더욱 최소화하도록 하고 작게하면 오차를 더욱 최소화하도록 만든다
regularization은 극단적으로 치우친 사람에 대해 계속 그 방향으로 극단적으로 추천하지 않고,
‘그 사람은 그런 경향이 있다’는 신중한 판단을 내리게 만든다
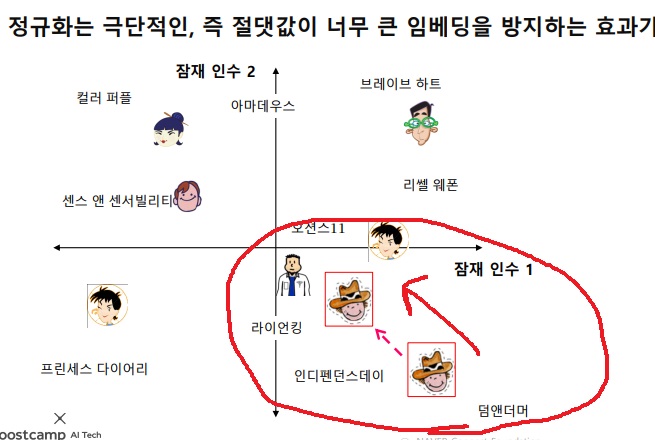
덤앤더머 쪽으로 치우친 사람에게 자꾸 그것과 비슷한 방향으로 추천하지 않고
모형이 이 사람은 저런 것을 좋아하긴하구나라고 참고정도할 수 있는 능력을 만들어준다
6. optimization
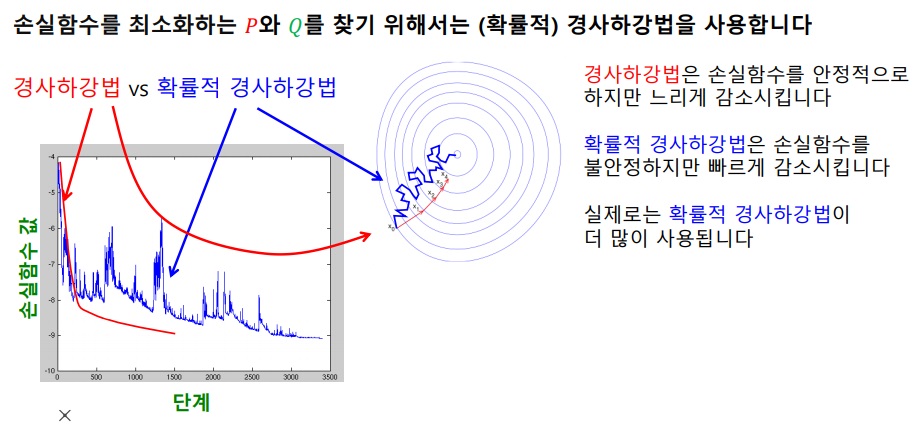
손실함수를 최소화하는 U,V를 찾기 위해 경사하강법을 사용한다.
일반적인 경사하강법은 신중하게 optimal로 접근하나 계산 속도가 너무 느리다.
그리고 local minimum으로 빠질 가능성도 높다.
확률적 경사하강법은 빠른 속도로 optimal로 접근하나 불안정하게 접근하여 최후에 그것이 optimal이라는 보장은 없다.
그러나 local minimum을 피할 가능성이 높다.
계산 속도가 빠르다는 점에서 확률적 경사하강법을 많이 쓴다.
'딥러닝 > recommendation system' 카테고리의 다른 글
| 시간에 따른 편향을 고려한 latent factor model (0) | 2024.07.19 |
|---|---|
| 사용자와 상품의 편향을 고려한 latent factor model (0) | 2024.07.17 |
| 추천시스템 평가 방법 (0) | 2024.07.05 |
| 추천시스템 기본이론2 -collaborative filtering- (0) | 2022.11.10 |
| 추천시스템 기본이론1 -content based recommendation- (0) | 2022.11.10 |

