E - Tree and Hamilton Path 2 (atcoder.jp)
E - Tree and Hamilton Path 2
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
트리의 어떤 정점 A에서 출발하여 모든 정점을 1번 이상 방문하고, 다시 정점 A로 돌아온다고 생각해보면,
만약 트리의 어떤 변을 제거하면 다음과 같이 2개의 연결성분이 생기고 출발점에서 다시 출발점으로 돌아올려면
두 연결성분을 서로 왔다갔다 해야하므로, 정확히 각 변을 2번 지나면 출발점에서 모든 노드를 1번 이상 방문하여 출발점으로 돌아올 수 있다
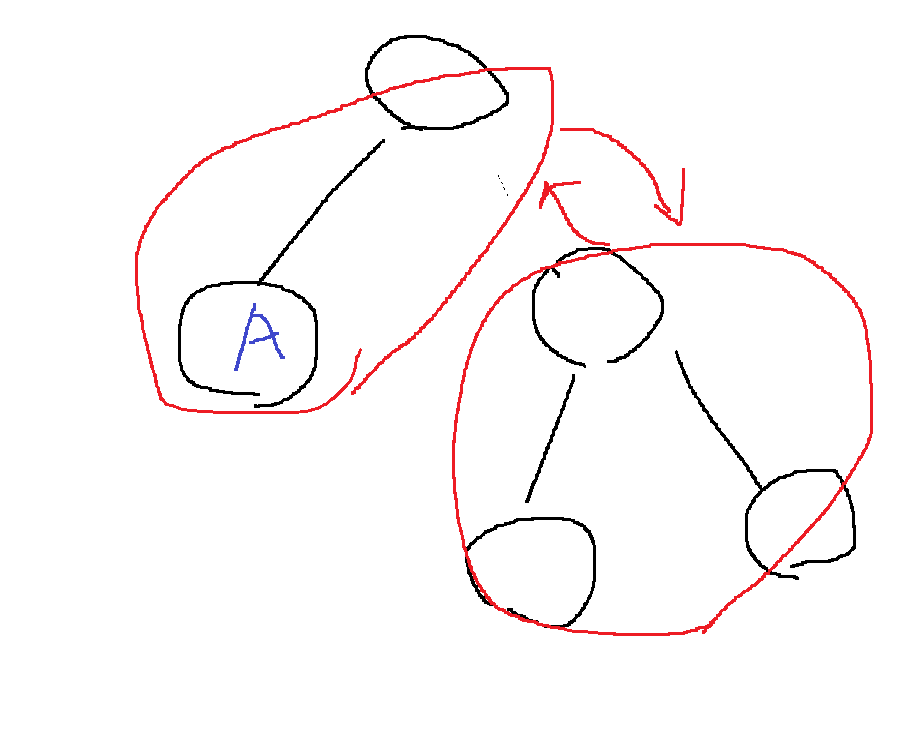
따라서 아무 정점에서 DFS를 수행하여 모든 정점을 순회하면, 각 변을 2번 방문하여 돌아올 수 있으므로
최소 이동거리는 $\sum_{i = 1}^{n-1} 2w_{i}$
시작점에서 모든 노드를 1번 이상 방문하고 다시 시작점으로 돌아오는 경로는,
어떤 시작점에서 모든 노드를 1번 이상 방문하여 어떤 마지막으로 방문한 정점까지 이동하고,
그 마지막 정점에서 다시 시작점으로 돌아오는 경로와 같다.
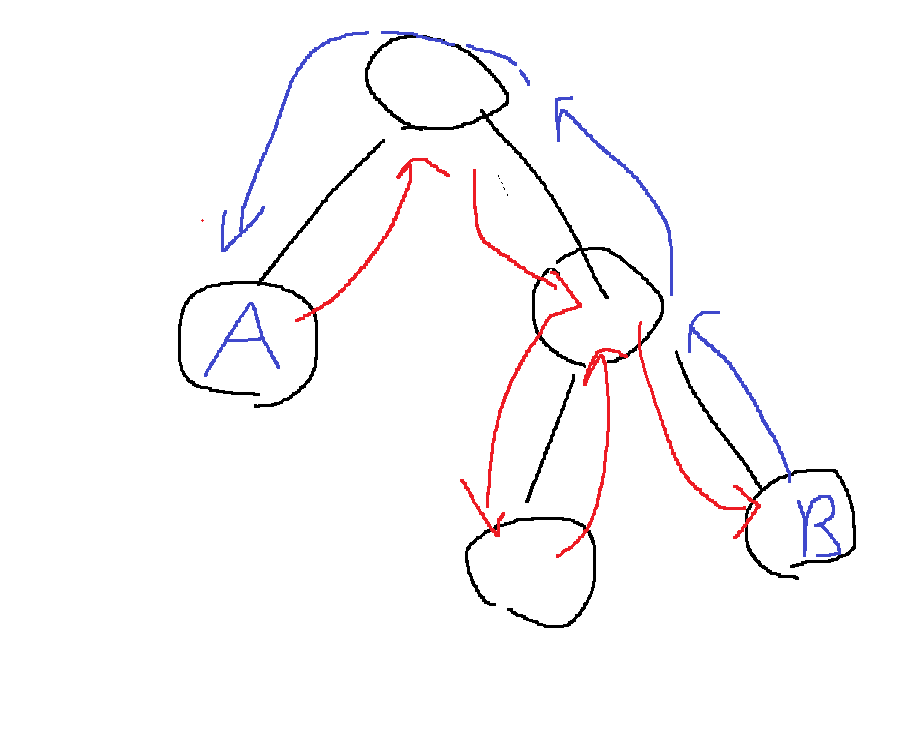
어떤 시작점에서 모든 정점을 1번 이상 방문하고 다시 돌아오는 거리의 최솟값은 $\sum_{i = 1}^{n-1} 2w_{i}$인데,
이것이 파란색과 빨간색의 합이다.
문제에서 원하는 것은 빨간색 거리의 합이 최소가 되길 원하는 것인데 $\sum_{i = 1}^{n-1} 2w_{i}$는 고정된 값이므로
파란색 거리가 최대가 되면 된다.
파란색 거리가 최대가 되는 것은 어떤 정점에서 다른 정점까지 가장 먼 거리이므로, 트리의 지름과 같다.
https://deepdata.tistory.com/1035
DFS 2번으로 트리의 지름을 구하는 방법
1. 문제 1967번: 트리의 지름 (acmicpc.net) 1967번: 트리의 지름 파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는
deepdata.tistory.com
모든 변의 거리 합은 쉽게 구할 수 있고 DFS 2번으로 트리의 지름을 구하는 방법은 이미 배웠으므로,
DFS 2번으로 이 문제를 해결할 수 있다
from sys import stdin,setrecursionlimit
setrecursionlimit(10**6)
def dfs(u,path):
global diameter, leaf
if diameter < path:
diameter = path
leaf = u
visited[u] = 1
for v,w in tree[u]:
if visited[v] == 0:
dfs(v,path+w)
v = int(input())
tree = [[] for _ in range(v+1)]
total = 0
for _ in range(v-1):
a,b,c = list(map(int,input().split()))
total += c
tree[a].append((b,c))
tree[b].append((a,c))
diameter = 0
visited = [0]*(v+1)
leaf = -1
dfs(1,0)
visited = [0]*(v+1)
dfs(leaf,0)
print(2*total - diameter)
atcoder에서 재귀라 PYPY가 느린것 같은데 그러면 Cpython으로 하면 통과함
'알고리즘 > DFS BFS 정복기' 카테고리의 다른 글
| BFS로 어떤 정수의 0과 1로만 이루어진 배수 찾기 (0) | 2025.01.28 |
|---|---|
| 퍼져나갈 수 있는지를 묻고 있지만 도달할 수 있는지를 계산해야하는 BFS (0) | 2025.01.25 |
| 트리 필수 테크닉3 - 모든 정점들 각각 가장 먼 거리를 2번의 DFS로 구하는 방법 (0) | 2023.12.21 |
| 트리 탐색 테크닉2 - 현재 노드에서 가장 먼 자식 노드까지의 거리 (0) | 2023.12.15 |
| 트리 탐색 필수 테크닉 - 자식 노드로 내려가서 얻은 value를 부모 정점으로 value 보내는 DFS 테크닉 (0) | 2023.12.13 |

