1. 문제
11429번: Tree
The input file contains the description of the tree. The first line of the input file contains one integer N, 2<=N<=50000. Each of the following (N-1) lines contains the description of the tree’s edges. Each edge is described by three positive integers.
www.acmicpc.net
2. 풀이
이전에는 하나의 정점에서 다른 정점까지 가장 먼 거리를 구하는 문제였는데
https://deepdata.tistory.com/1035
DFS 2번으로 트리의 지름을 구하는 방법
1. 문제 1967번: 트리의 지름 (acmicpc.net) 1967번: 트리의 지름 파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는
deepdata.tistory.com
이번에는 각 정점에서 가장 먼 거리를 모두 구해야하는 문제
당연히 정점이 5만개라 각 정점마다 DFS를 하면 시간초과
이 문제는 먼저 각 정점 v를 루트로 하는 서브트리에서 자식까지 가장 먼 거리를 1번의 DFS로 모두 구해준다
https://deepdata.tistory.com/1050
트리 탐색 필수 테크닉 - 자식 노드로 내려가서 얻은 value를 부모 정점으로 value 보내는 DFS 테크닉
1. 문제 30414번: 투스타 춘배 (acmicpc.net) 30414번: 투스타 춘배 춘배 나라에는 $1$부터 $N$까지의 번호가 붙은 $N$개의 산, 그리고 두 산 사이를 이동할 수 있는 $N-1$개의 길이 있다. 게다가 임의의 두 산
deepdata.tistory.com
https://deepdata.tistory.com/1055
트리 탐색 테크닉2 - 현재 노드에서 가장 먼 자식 노드까지의 거리
1. 문제 19542번: 전단지 돌리기 (acmicpc.net) 19542번: 전단지 돌리기 현민이는 트리 모양의 길 위에서 오토바이를 타고 전단지를 돌리려고 한다. 현민이의 목표는 케니소프트에서 출발하여 모든 노드
deepdata.tistory.com
정점 u에 대하여, 자식 v를 순회하는데...
일단 dfs(v)로 계속 들어간 다음...
리프 노드 v의 depth는 0으로 두면서.. return하여 올라오는데.. 간선의 가중치가 w이므로..
depth[u] = depth[v] + w로 할 수 있다.
그런데, u에서 v로 내려가는 길은 1가지가 아니니까... 가장 긴 거리를 구할려면 최댓값으로 갱신해줘야하니까
depth[u] = max(depth[u], depth[v] + w)
#u에서 자식까지 가장 먼 거리
def find_depth(u):
for v,w in tree[u]:
if visited[v] == 0:
visited[v] = 1
find_depth(v) #u에서 자식 v로 계속 내려간 다음,
#리프 노드부터 w씩 증가시키면서 올라오는데
#u에서 내려가는 길은 여러가지일 수 있으니, max값으로 갱신
depth[u] = max(depth[u],depth[v]+w)
트리의 지름을 구할때, 한 정점에서 한쪽 방향으로 가장 먼 거리의 노드를 구하고,
그 노드에서 가장 먼 거리의 노드까지 거리를 구해주면.. 그것이 지름이라는 사실을 이용해서
https://deepdata.tistory.com/1035
DFS 2번으로 트리의 지름을 구하는 방법
1. 문제 1967번: 트리의 지름 (acmicpc.net) 1967번: 트리의 지름 파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는
deepdata.tistory.com
비슷한 접근으로 한쪽 노드에서 자식까지 가장 먼 거리를 depth에 모두 채웠는데,
이제 위쪽으로 가장 먼 거리를 dist로 모두 채울려고 한다
어떤 정점 u에 대하여 u에서 가장 먼 자식까지의 거리 h1, 두번째로 먼 자식까지의 거리 h2를 구하면

어떤 정점 u에서 위쪽으로 가장 먼 거리를 dist[u] = h라고 하자.
u의 자식 v는 다음과 같은 2가지 경우가 가능하다.
먼저 v가 가장 먼 거리인 h1 위에 놓여있는 경우..

이러면 정점 v의 자식까지 가장 먼 거리는 h1-w이고, v의 위쪽으로 가장 먼 거리는..?
dist[u] = h와 u에서 자식까지 2번째로 가장 먼 거리 h2중 더 큰 값 max(h,h2)에 v에서 u까지 거리 w의 합이다.
dist[v] = max(h,h2)+w
두번째로는 다음과 같이 v가 가장 먼 거리 h1 위에 놓여있지 않은 경우
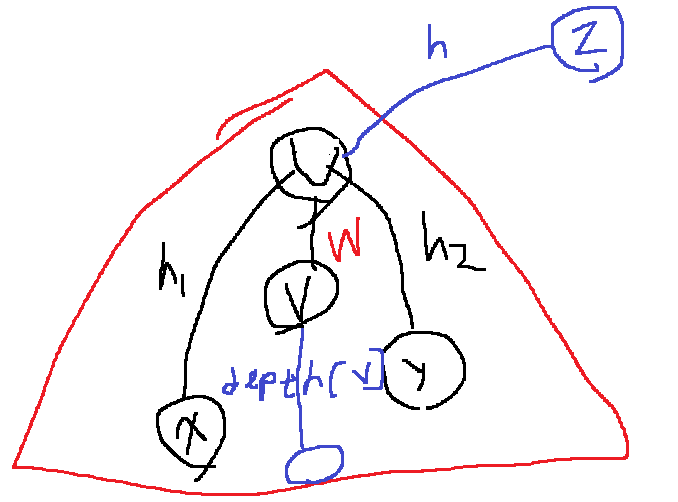
이 경우, v에서 위쪽으로 가장 먼 거리는..?
h1과 h2중 h1이 더 크므로 h1과 u에서 위쪽으로 가장 먼 거리 h중 더 큰 값 max(h,h1)에 v에서 u까지 거리 w의 합이다.
dist[v] = max(h1,h) + w
def dfs(u):
#u에서 자식까지 가장 먼 거리 d1, 두번째로 먼 거리 d2를 구한다
d1 = 0
d2 = 0
#u의 자식 v를 모두 순회하여, v에서 자식까지 가장 먼 거리 depth[v]에
#v에서 u까지 거리 w의 합 depth[v]+w중 1번째로 큰 값, 2번째로 큰 값을 구한다.
for v,w in tree[u]:
if visited[v] == 0:
x = depth[v]+w
if d1 < x: #x가 d1보다 크면,
d2 = d1 #이전 d1은 2번째로 큰 값이고
d1 = x #x는 새로운 가장 큰 값
elif d2 < x: #x가 d1보다 작은데, d2보다 크다는 것은.. x가 2번째로 큰 값
d2 = x
#d1,d2를 구했으면, v에서 위쪽으로 가장 먼 거리 dist[v]를 구한다.
for v,w in tree[u]:
if visited[v] == 0:
visited[v] = 1
x = depth[v] + w
#u의 자식 v에 대하여...
#가장 먼 거리 d1이 depth[v]+w와 같다는 것은 v가 d1위에 놓여있다
#이 경우 v에서 위쪽으로 가장 먼 거리는.. dist[v] = max(dist[u],d2)+w
if d1 == x:
dist[v] = max(dist[u],d2)+w
#d1이 x와 다르다면, v는 d1위에 있지 않다.
#v에서 위쪽으로 가장 먼 거리는.. dist[v] = max(dist[u],d1)+w
else:
dist[v] = max(dist[u],d1)+w
#다음 자식으로 이동
dfs(v)
여기서 처음에 u의 자식 중 가장 먼 두 거리를 구할때, 방문되지 않은 정점 v를 찾고, 방문하지는 않아야한다.
'방문되지 않은 정점 v'라는 말이 바로 u의 자식이기 때문이다.
d1,d2를 찾고 나서는, dist[v]를 찾아야하는데, 트리는 루트부터 시작해서 계속 내려가는 형태이므로
이제는 방문되지 않은 정점 v는 dist[v]를 찾으면 방문시켜야한다.
depth배열과 dist배열을 모두 채웠다면.. 어떤 정점 v에서 가장 먼 거리는?
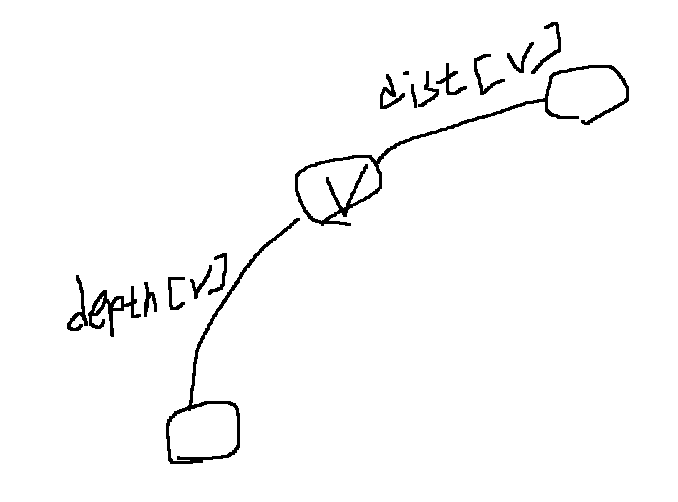
depth[v] + dist[v]??는 다른 정점에서 다른 정점까지 가장 먼 거리고...
v에서 가장 먼 거리는 depth[v]와 dist[v]중 더 큰 값이겠지
1번을 루트로 시작해서 dist 배열을 찾는다.
루트로 시작하는 정점 1번의 dist값은? 당연히 0이다.
루트에서 위쪽으로 가장 먼 거리는 0이니까
n = int(stdin.readline())
tree = [[] for _ in range(n+1)]
for _ in range(n-1):
u,v,w = map(int,stdin.readline().split())
tree[u].append((v,w))
tree[v].append((u,w))
depth = [0]*(n+1)
dist = [0]*(n+1)
#정점 u에서 자식까지 가장 먼 거리 depth를 구한다
visited = [0]*(n+1)
visited[1] = 1
find_depth(1)
#정점 u에서 위쪽으로 가장 먼 거리 dist를 구한다
visited = [0]*(n+1)
visited[1] = 1
dfs(1)
#정점 u에서 가장 먼 거리는, depth와 dist중 더 큰 값이다.
for i in range(1,n+1):
print(max(dist[i],depth[i]))
'알고리즘 > DFS BFS 정복기' 카테고리의 다른 글
| 퍼져나갈 수 있는지를 묻고 있지만 도달할 수 있는지를 계산해야하는 BFS (0) | 2025.01.25 |
|---|---|
| 트리에서 임의의 노드에서 모든 노드를 적어도 1번 이상 방문하는데 걸리는 최소 거리 (0) | 2024.07.11 |
| 트리 탐색 테크닉2 - 현재 노드에서 가장 먼 자식 노드까지의 거리 (0) | 2023.12.15 |
| 트리 탐색 필수 테크닉 - 자식 노드로 내려가서 얻은 value를 부모 정점으로 value 보내는 DFS 테크닉 (0) | 2023.12.13 |
| 트리에서 두 노드 사이 유일한 경로를 찾는 방법 (0) | 2023.12.05 |

