1. 문제
30414번: 투스타 춘배
춘배 나라에는 $1$부터 $N$까지의 번호가 붙은 $N$개의 산, 그리고 두 산 사이를 이동할 수 있는 $N-1$개의 길이 있다. 게다가 임의의 두 산 사이를 항상 길을 통해 이동할 수 있다고 한다. 즉, 산을
www.acmicpc.net
2. 풀이
현재 산의 높이가 원하는 높이보다 작다면 흙을 차이만큼 구매하는게 좋고,
높다면 깎아내리는게 좋을 것이다.
근데 문제는 병사 1명이 u번에서 v번으로 내려갈때, 깎아내린 산 크기 X만큼을 가져가는데
u번에서 v번 경로가 아닌 다른 경로로 X만큼을 가져갈 수 없다는게 문제
트리 탐색은 DFS로 가능한데 v로 들어가기 전에 visited[v] = 1로 체크하고 나와서 visited[v] = 0으로 안해준다면
자식에서 부모로 가지는 않는다
부모에서 자식으로만 갈 수 있게 해줌
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
현재 정점에서 원하는 높이 B[u]와 현재 산의 높이 A[u]의 차이는 양수라면 구매해야하는 흙의 양이고,
음수라면 다음 정점으로 가지고 갈 수 있는 흙의 양이 된다.
def dfs(u):
c = B[u] - A[u]
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
u에서 v로 dfs() 쭉 내려가다가, 리프노드에 도달한다면 for v in tree[u]:가 수행되지 않고...
c = B[u] - A[u]만 수행되고 끝인데,
리프노드에서 흙을 구매해야하는 경우가 있을 수 있고 이를 부모 정점으로 넘겨줘야한다
이러면 c를 return해준다면...
def dfs(u):
c = B[u] - A[u]
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v) #<--2
return c #<--1
u번 노드에서 시작해서 v번 노드로 쭉 내려가다가, 더 이상 내려갈 수 있는 노드가 없으면 1번의 return c가
2번으로 올라오는..
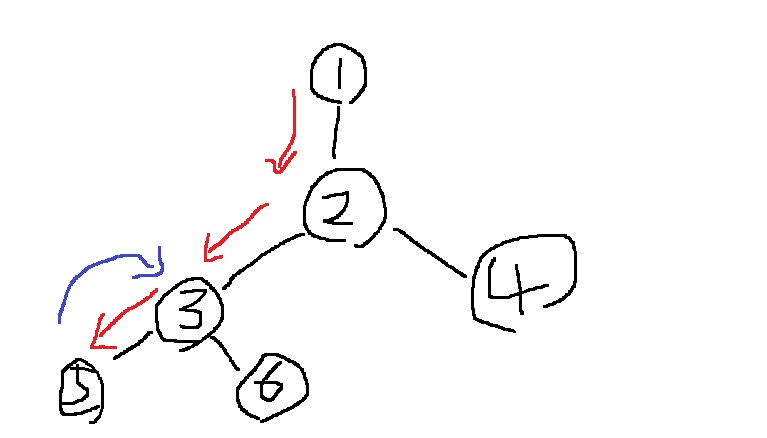
예를 들어 1번부터 시작해서 재귀 스택에 dfs(1),dfs(2),dfs(3),dfs(5)가 순서대로 쌓이면서,
5번에서는 더 이상 내려갈 수 없으므로, return하기 시작
5번의 c값이 3번으로 올라감
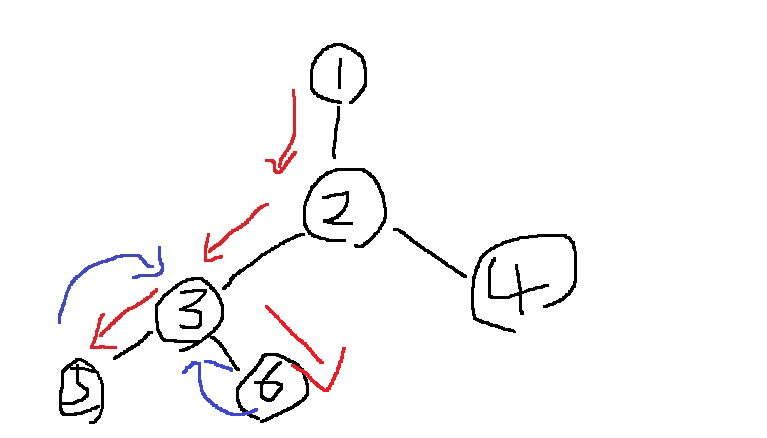
그러면 3번에서 6번으로 내려가서 dfs(1),dfs(2),dfs(3),dfs(6)이 쌓이고 6에서 내려갈 수 없어서
6번에서 return되어 6번의 c값이 3번으로 올라감
근데 문제는, 산을 깎아내려서 보유하고 있는 흙의 양은 뒤로 가지고 갈 수 없으므로
c < 0라면 0을 return해서 부모 정점으로 넘겨주면 안된다
def dfs(u):
c = B[u] - A[u]
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
if c < 0:
c = 0
return c
예제를 보고 구체적으로 한번 생각해보면 1번에서 탐색을 시작해서
c = 2를 가지고 자식 정점 v를 순회하기 시작
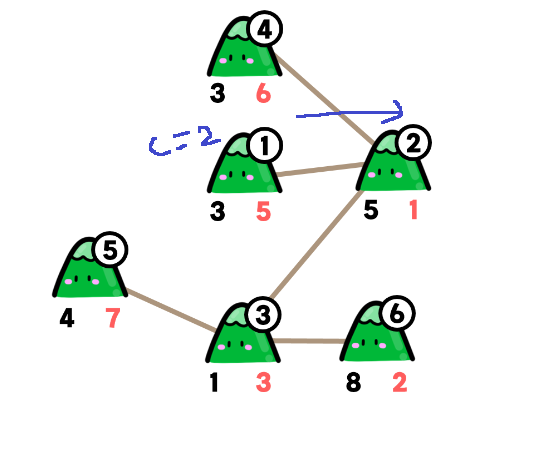
2번 정점으로 들어가면... c = -4가 된다
다시 3번 정점으로 들어가면 c = 2가 된다
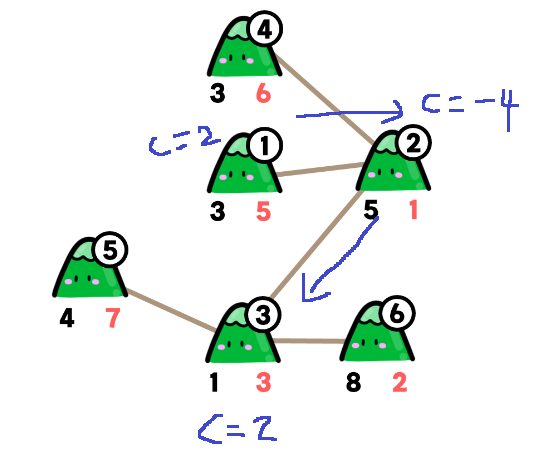
다시 5번 정점으로 내려가면 c = 3인데
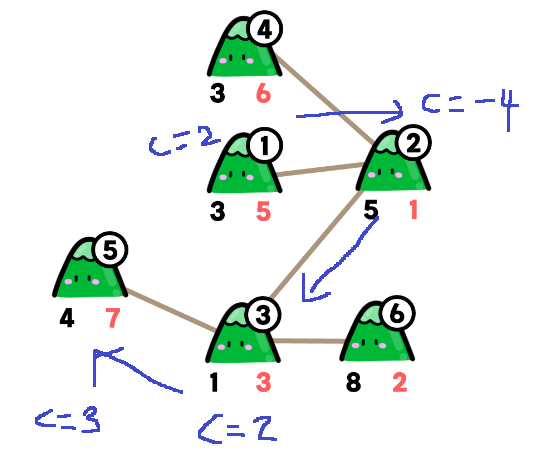
여기서 더 이상 내려갈 수 없으므로 c = 3은 구매해야하는 양이고 부모 정점으로 넘겨준다면...
그러면 3번 정점에서 c = 5가 되어야한다.

그리고 6번 정점으로 내려가주면.. c = -6으로 산을 깎아내려서 보유하고 있는 흙의 양인데
뒤로 돌아가서 가지고 갈 수는 없으므로, 부모 정점으로 넘겨줄 때 c = 0으로 return 시켜줘야한다.
따라서 3번 정점에서 여전히 c = 5이고
이제 더 내려갈 수 없으니 dfs(3)도 return되어 2번 정점으로 c = 5를 넘겨준다
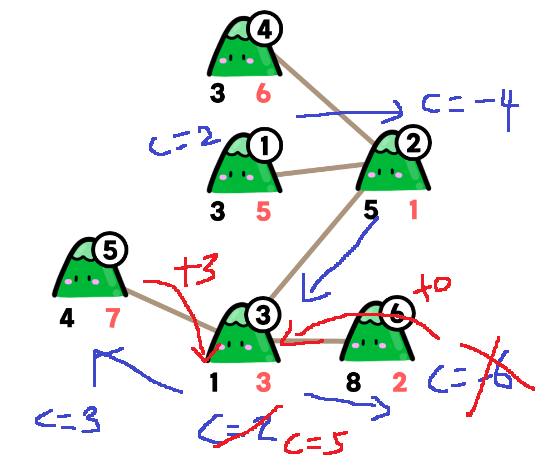
그러면 2번 정점에서 c = 1이 된다.
이것은 마치 반대로 생각해보면.. 2번 정점에서 4만큼 깎아내려서 흙을 4만큼 보유하고
3번 정점, 5번 정점, 6번 정점으로 내려가서
3번 정점에서 보유한 4중에 2만큼 써서 산 높이를 3으로 올려주고,
5번 정점에서 2만큼 쓰고 1만큼 구매해서 7로 맞춰주고
6번 정점에서는 아무것도 쓰지 않고 그냥 6만큼 깎아내린것과 같다.
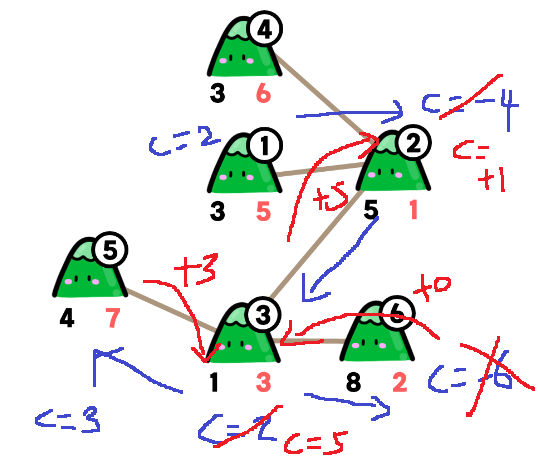
그리고 2번 정점에서 4번 정점으로 내려간다면...
4번 정점에서 c = 3인데 더 이상 내려갈 수 없으니 이를 부모 정점 2번으로 넘겨주고
2번 정점에서 c = 4가 된다.
더 내려갈 수 없으니 2번 정점에서 return되어 1번 정점으로 c = 4를 넘겨준다.
그래서 1번 정점에서 c = 6이 되어.. 최종적으로 c = 6을 dfs(1)이 return하게 된다.
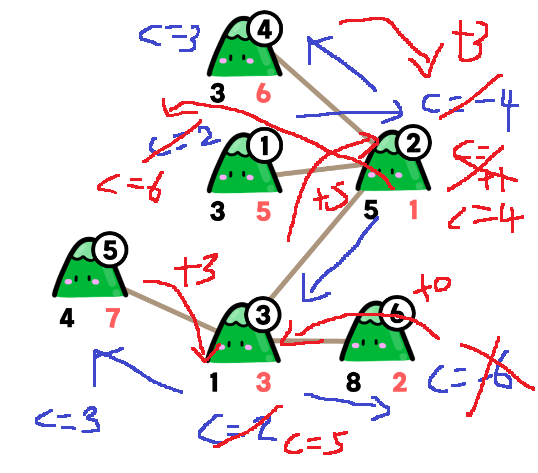
그래서 dfs()함수 구조는 for문 안에서 dfs() return값을 버리지 말고
c에 계속 누적해주면... 자식 정점까지 내려가서 얻은 value를 부모 정점으로 넘겨주는 형태를 취하게 된다.
from sys import stdin,setrecursionlimit
setrecursionlimit(200000)
def dfs(u):
#양수면 현재 u에서 구매해야하는 흙의 양
#음수면 현재 u에서 다음 정점으로 가지고 갈 수 있는 흙의 양
c = B[u] - A[u]
#자식 정점으로 이동
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
#자식 정점 v에서 구매해야하는 흙의 양을 더해주는데
#현재 정점에서 산을 깎아 내린 경우, c가 음수이고
#return된 자식 정점에서 구매해야하는 흙의 양에 충당시켜주게 된다
#1(c=2) > 2(c=-4) > 3(c=2) > 5(c=3 return) > 3(c=2+3=5) > 2(c=-4+5=1) > 1(c=2+1=3)
#1(c=2) > 2(c=-4) > 3(c=2) > 6(c=-6 > 0 return) > 3(c=2) > 2(c=-4) > 1(c=2)
#1(c=2) > 2(c=-4) > 4(c=3 return) > 2(c=1+3) > 1(c=2+1+3=6)
c += dfs(v)
#더 이상 다음 정점으로 이동할 수 없는 경우(리프노드에 도달)
#흙을 보유하고 있는 경우(c < 0) = 모든 흙을 버려야함
#구매해야하는 흙인 경우 부모 정점으로 부담시켜줘야함
if c < 0:
c = 0
return c #부모 정점으로 흙을 보내기
n,p = map(int,stdin.readline().split())
A = [0] + list(map(int,stdin.readline().split()))
B = [0] + list(map(int,stdin.readline().split()))
tree = [[] for _ in range(n+1)]
for _ in range(n-1):
u,v = map(int,stdin.readline().split())
tree[u].append(v)
tree[v].append(u)
visited = [0]*(n+1)
visited[p] = 1
print(dfs(p))
3. 문제2
16437번: 양 구출 작전
2, 3, 5번에 사는 모든 양들은 1번 섬으로 갈 수 있지만 7번 섬에 사는 양들은 1번 섬으로 가기 위하여 6번 섬을 거쳐야 하는데 6번 섬에 사는 늑대들의 수가 7번 섬에 사는 양들의 수보다 많으므로
www.acmicpc.net
4. 풀이
1번 섬으로 가는 경로가 유일하면서 간선이 n-1개라 트리 구조의 형태를 가지고 있고
각 정점에서 1번 노드로 양들이 돌아오는데, 어떤 노드에는 늑대가 있어서..
늑대를 만나게 된다면 그만큼 늑대한테 먹히게 된다
이 문제도 결국 1번 노드에서 시작해서 모든 노드를 탐색하다가 각 노드에서 양을 가지고 다시 1번으로 보내줘야하는 형태
위의 테크닉으로 자식 정점에서 부모 정점으로 value를 넘겨주는 구조를 만들면 되겠다
현재 u번 노드에 양이 sheep = 0이고 u번에서 v번 자식으로 이동할건데, sheep을 return하고,
sheep에 dfs()함수 값을 누적해준다면... 자식 노드의 sheep을 부모 노드로 보내주는 형태가 된다
def dfs(u):
sheep = 0 #u번 노드의 양의 수
for v in tree[u]:
sheep += dfs(v) #자식 노드의 양을 모두 가져오고
return sheep
이제 현재 노드에 양이 있는지, 늑대가 있는지 체크하고, 현재 노드가 양이라면 그대로 누적해주면 될거고
양이 아니라면, 늑대 수만큼 감소시켜주면 될것이다
늑대 수가 더 많다면 양의 수는 0으로 될거고
from sys import stdin,setrecursionlimit
setrecursionlimit(200000)
def dfs(u):
sheep = 0 #u번 노드의 양의 수
for v in tree[u]:
sheep += dfs(v) #자식 노드의 양을 모두 가져오고
#현재 노드가 양이 있는지 늑대가 있는지
if value[u][1] != 0:
if sheep <= value[u][1]:
sheep = 0
else:
sheep -= value[u][1]
else:
sheep += value[u][0]
return sheep #부모 노드로 return
n = int(stdin.readline())
tree = [[] for _ in range(n+1)]
value = [[0,0] for _ in range(n+1)]
for i in range(2,n+1):
t,a,p = stdin.readline().rstrip().split()
tree[(int(p))].append(i)
if t == 'W':
value[i] = [0,int(a)]
else:
value[i] = [int(a),0]
print(dfs(1))
'알고리즘 > DFS BFS 정복기' 카테고리의 다른 글
| 트리 필수 테크닉3 - 모든 정점들 각각 가장 먼 거리를 2번의 DFS로 구하는 방법 (0) | 2023.12.21 |
|---|---|
| 트리 탐색 테크닉2 - 현재 노드에서 가장 먼 자식 노드까지의 거리 (0) | 2023.12.15 |
| 트리에서 두 노드 사이 유일한 경로를 찾는 방법 (0) | 2023.12.05 |
| DFS도 재귀보다는 반복문으로 구현 연습하기1 (0) | 2023.08.19 |
| DFS 재활훈련 - return이 있는 DFS 작성하기 연습 + 트리의 경로 유일성 배우기 (0) | 2023.02.13 |

