주어진 그래프의 개별 정점에서부터 점점 군집을 병합해가는 상향식 알고리즘
1. first phase - modularity optimization
처음 주어진 상태에서는 개별 node 1개씩이 하나의 군집이라고 생각
특정 node i를 그것의 이웃(neighbor)인 j에 병합시키면서 modularity의 변화량을 계산함
원래 상태의 modularity와 이웃인 j에 병합시킨 뒤 modularity의 차이를 계산한다.
병합시키면 군집이 생기니까 modularity는 최소한 감소하지는 않음
이 때 최대로 modularity가 증가하는 이웃 j가 있을 것인데 그곳에 i를 포함시킨다.
증가하는 경우가 없다면 어떠한 곳에도 포함시키지 않는다.
다시 다른 node v를 선택하여 위 과정을 반복, 모든 node에 대해 반복적으로 수행하여 modularity의 변화가 없으면 첫번째 phase를 종료함
어떤 노드 순서로 하느냐는 modularity 변화에 큰 차이가 없다고 하는데 계산 시간에는 영향을 줄 수도 있다고 말함
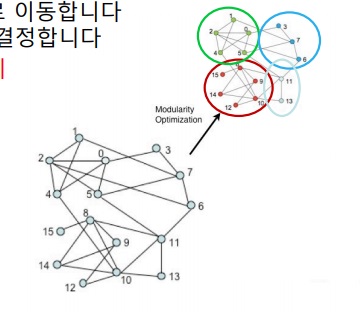
2. second phase - community aggregation
이제 형성된 군집을 하나의 node로 만든다.
이 때 군집내 link weight를 합쳐서 하나의 self-loop link로 만든다

군집을 하나의 node로 만들고
이 때 군집내 link weight를 모두 합쳐 하나의 weight로 만들어서 self-loop로 만들었다는 것이 보인다
first phase와 second phase를 합쳐 하나의 pass라고 부르자.
pass시킬때마다 modularity를 계산한다.
pass를 반복하면 modularity가 점점 증가할텐데(군집이 증가하니까)
(pass끝나고 다음 pass의 first phase를 수행할때) modularity가 더 이상 증가하지 않으면 알고리즘을 종료한다.

주어진 그래프의 modularity 계산하여 Q0
first phase로 modularity optimization 수행,
다음 second phase로 community aggregation 수행, 이것을 하나의 pass라고 명명
pass후 Q1계산, Q0에서 Q1이 증가했는지 본다.
증가했다면 두번째 pass 수행, 다시 Q2를 계산하고 Q1에서 비교한다
위 과정을 반복하여 (다음 pass의 first phase에서) modularity가 증가하지 않으면 종료한다.
3. example of Louvain algorithm

두 군집 사이의 다리 역할을 하는 곳에 하나의 군집이 있는데 두 언어를 혼용하는 사람들의 모임일 가능성이 높다
'딥러닝 > Graph' 카테고리의 다른 글
| 그래프 전파 모형3 - 전파 최대화 문제(influence maximization) (0) | 2024.09.02 |
|---|---|
| 군집을 찾는 알고리즘1 - Girvan-Newman algorithm (0) | 2024.09.01 |
| 그래프 전파 모형2 - 확률적 전파 모형(Stochastic cascade model) (0) | 2024.05.15 |
| 그래프 전파 모형1 - 선형 임계치 모형(linear threshold model) (0) | 2024.05.10 |
| 그래프를 다루는 파이썬의 NetworkX 라이브러리 맛보기 (0) | 2023.08.07 |

