군집을 찾는 알고리즘1 - Girvan-Newman algorithm

1. idea

 

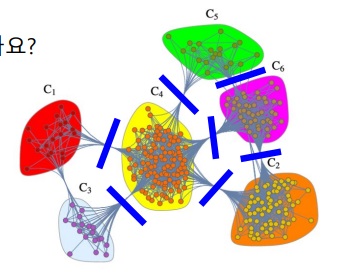
군집을 찾는 대표적인 하향식 알고리즘으로 전체 그래프에서 시작하여 군집들이 서로 분리되도록 link를 순차적으로 제거함

 

서로 다른 군집을 연결하는 다리 역할을 하는 link를 먼저 제거해나가야 군집들이 분리 될 것이다.

 

다리 역할을 하는 link를 제거해나가야 군집들이 서로 분리

 

 

2. betweenness centrality

 

그래프의 임의의 두 node의 최단 경로 위에 특정 link가 몇번이나 놓이는지 계산

 

betweenness centrality를 구하는 방법

 

 

 

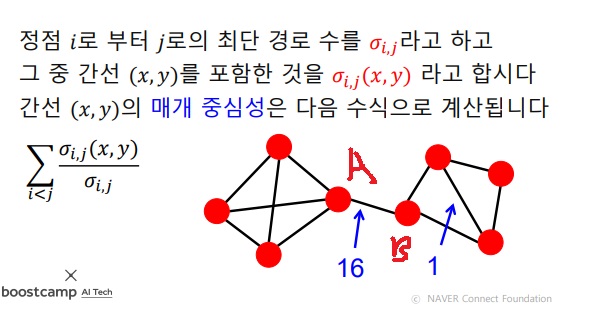
link A-B는 양 옆 4개의 node중 하나를 선택하여 만든 최단 경로에 모두 존재해야하므로 4*4=16가지가 있다.

 

따라서 그림을 보면 직관적으로 betweenness centrality가 높은 link는 두 군집을 연결하는 다리 역할을 할 가능성이 높다.

 

빨간 선이 다리 역할을 하는 link이며 실제로 매개 중심성이 높다고 한다

 

 

3. algorithm

 

주어진 그래프에서 모든 link의 매개 중심성을 계산한다.

 

예상대로 다리 역할을 하는 7번과 8번사이 매개 중심성이 가장 높다

 

 

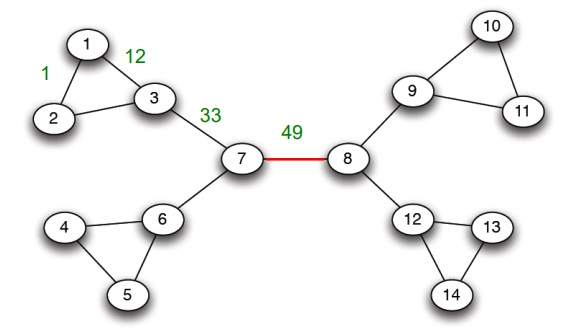
그리고 가장 매개 중심성이 높은 link를 모두 제거한다.

 

그러니까 매개 중심성이 가장 높은 link가 여러개면 여러개 모두 제거하라는 말이다.

 

 

 

다시 제거된 상황(위와 같은 상황)에서 매개 중심성을 다시 계산한다.

 

그리고 매개 중심성이 가장 높은 link를 모두 제거한다

 

 

 

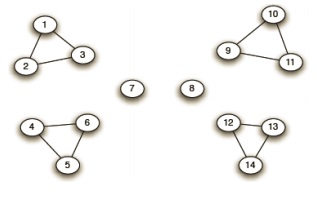
모든 link가 제거될 때까지 위와 같은 과정을 반복한다.

 

 

 

 

4. optimization

 

link를 어느 정도 제거해야 최적으로 잘 찾은 군집이라고 할 수 있을까?

 

granularity는 세분화된 정도?를 의미한다고 한다

 

 

당연하게도 군집성(modularity)이 최대가 되는 경우가 찾고자 하는 최적

 

Girvan-Newman algorithm을 수행하는 각 상황에서 주어진 그래프의 연결요소(connected component)를 군집으로 가정하고 군집성을 계산한다

 

군집성이 최대가 되는 지점의 요소들을 알고리즘이 끝나면 복원하여 그 때 연결요소들을 군집으로 간주한다

 

 

 

제거되는 link에 따라 군집성을 계산하고

 

알고리즘이 끝나면 군집성이 최대가 되는 지점의 그래프들을 복원해서

 

연결요소들을 군집으로 간주함