1. 문제
코딩테스트 연습 - 도넛과 막대 그래프 | 프로그래머스 스쿨 (programmers.co.kr)
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2. 풀이
핵심은 눈치 잘 챘는데.. 시간의 압박에 못이겨서 그런건지 시간초과에서 못벗어났다..
다시 풀어보니까 시간복잡도를 생각해서 기본에 충실하게 DFS 그래프 탐색을 구현한다면 생각보다 쉽게 풀 수 있더라고
평면에 도넛, 막대, 8자모양 그래프가 여러개 있는데..
이 그래프와 무관한 하나의 정점을 생성하고 이 정점과 각 그래프의 임의의 정점 중 하나에 연결시켰다
무관한 하나의 정점 번호와 도넛, 막대, 8자모양 그래프의 수를 구하는게 문제
무관한 하나의 정점은 어떻게 구할 수 있는가?
그 정점에서 그래프 방향으로 연결시켰기 때문에..
주어진 간선 정보로부터 모든 정점 중에 들어오는 간선이 존재하지 않고 나가는 간선만 존재하는 정점이 존재할 것
특히 평면 위에 도넛, 막대, 8자모양 그래프는 2개 이상이기 때문에 들어오는 간선이 존재하지 않고,
나가는 간선이 2개 이상 있는 정점이 '무관한 하나의 정점'이다

그래프 특징을 살펴보면서 다른 정점도 이렇게 '들어오는 간선이 0개', '나가는 간선이 2개 이상'인 경우가 될 수 있는지
생각해봐야한다.
도넛, 8자 모양 그래프는 모든 정점이 들어오는 간선이 존재한다.
막대 모양 그래프는 첫 정점이 나가는 간선만 존재하는데.. '무관한 정점'이 이 정점과 연결되었다고 가정하면..
들어오는 간선이 1개, 나가는 간선이 1개이다.
연결되지 않았다고 가정한다면 들어오는 간선이 0개, 나가는 간선이 1개이다.
따라서 '무관한 정점'만 '들어오는 간선이 0개', '나가는 간선이 2개 이상'이 될 수 있다.
이건 잘 파악했어
따라서 먼저 할 것은 간선 정보로부터 각 정점의 나가는 간선, 들어오는 간선의 개수를 세는 것이다
def solution(edges):
answer = [0,0,0,0]
n = 0
graph = [[] for _ in range(1000001)]
in_edge = [0]*(1000001)
out_edge = [0]*(1000001)
for a,b in edges:
if n < a:
n = a
if n < b:
n = b
graph[a].append(b)
in_edge[b] += 1
out_edge[a] += 1
for i in range(1,n+1):
if in_edge[i] == 0 and out_edge[i] >= 2:
start = i
break
다음에 다음과 같이 생긴 하나의 그래프를 탐색한다고 생각해보자.
'무관한 하나의 정점' 번호는 확실히 알고 있으니 여기서부터 이 전체 그래프를 탐색해서 1,2,3,... 각 부분 그래프가
어떤 그래프인지 판단하고 싶은 것이다.

다음에 알아볼 수 있는 것은 각 그래프별로 어떤 특징을 가지는지 파악하는 것이다.
그래프를 탐색하는데, 이 그래프가 무엇인지 알려면 해당 그래프만이 가지는 고유한 특징이 분명히 있을 것
도넛 모양 그래프는 각 정점이 '들어오는 간선 1개', '나가는 간선 1개'로 이루어짐

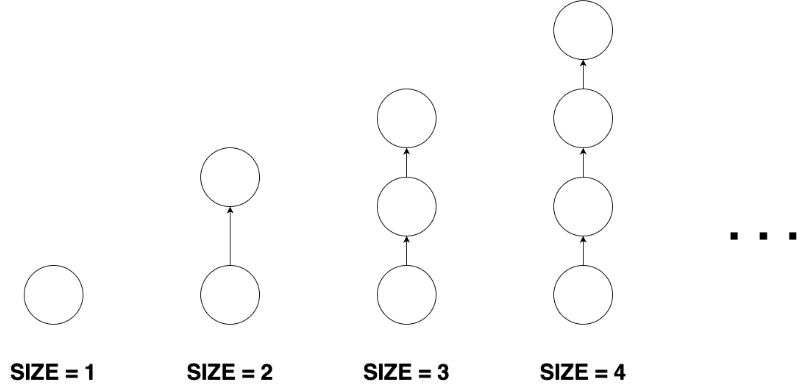
막대 모양 그래프는, '들어오는 간선 1개', '나가는 간선 1개'인 정점, '들어오는 간선 1개'인 정점
'나가는 간선 1개'인 정점으로 구성되어 있다
크기가 1인 경우는 들어오는 간선, 나가는 간선이 모두 없다.
크기가 2인 경우는 들어오는 간선, 나가는 간선이 각각 1개인 정점이 없다.
8자 모양 그래프는 정점이 '들어오는 간선 1개', '나가는 간선 1개'로 이루어져 있는데..
유일하게 하나의 정점만이 '들어오는 간선 2개', '나가는 간선 2개'로 구성되어 있다.

여기서 시험 당시에 생각 했던건
'무관한 정점'에서 각 그래프의 어떤 정점에 간선이 연결되어있을까? 모든 가능성을 고려했다는건데... 이래서 문제가 됐다
예를 들어 8자 모양 그래프는.. 현재 '들어오는 간선 2개', '나가는 간선 2개'인 정점 1개와 나머지는 '들어오는 간선 1개', '나가는 간선 1개'인 정점으로 구성되어 있는데
만약 들어오는 간선 2개, 나가는 간선 2개인 정점에 연결되면 8자 모양 그래프는..
들어오는 간선 3개, 나가는 간선 2개인 정점이 될 것이고 '들어오는 간선 1개','나가는 간선 1개'에 연결 되면..
'들어오는 간선 2개', 나가는 간선 1개'인 정점이 될 것이고..
그래서 '무관한 정점'에서 연결된 정점들을 순회해서,
각 정점부터 시작하는 DFS를 수행하면.. 이 정점 밖으로는 나갈 수 없으니까..
해당 부분 그래프만 순회할 수 있을 것이고.. 부분 그래프를 순회하면서..
들어오는 간선, 나가는 간선 수가 특정한 개수인 정점이 발견되면 이 그래프는 '8자 모양 그래프다' 이런식으로 했는데
근데 문제는 '들어오는 간선 2개', '나가는 간선 1개'인 경우는 모든 그래프가 가능하다는 것임
정점 수가 100만개나 되다 보니까 탐색하다가 '들어오는 간선 3개', '나가는 간선 2개'같이 확실히 구별되는 경우가
빨리 발견되면 다행이겠지만 최악의 경우에는 시간이 너무 오래걸릴 수 있다는게 문제
어떻게든 최대로 커팅해도 시간초과나더라
----------------------------------------------------------------------------------------------------------------------------------------------
핵심은 '무관한 정점'에서 각 그래프에 연결된 간선을 제거해버리는 것이다
for v in graph[start]:
in_edge[v] -= 1
이렇게 하고 1번부터 N번 정점까지 순회해서, 아직 방문하지 않은 정점이라면 해당 정점에서 DFS 탐색을 한다.
특정 정점은 오직 하나의 부분 그래프 내에 존재하기 때문에 DFS 시작을 한다면...
순회할때마다 각 정점이 가지는 들어오는 간선, 나가는 간선의 개수를 체크한다.
만약에 한번이라도 '들어오는 간선 2개', '나가는 간선 2개'인 경우가 발견된다면 8자 모양 그래프
'들어오는 간선 0개', '나가는 간선 1개'인 경우 혹은 '들어오는 간선 1개', '나가는 간선 0개'인 경우,
'들어오는 간선 0개', '나가는 간선 0개'인 경우<크기 1인 경우>가 발견된다면 막대 모양 그래프..
아예 발견이 안된다면 이 그래프는 도넛 모양이다.
그러니까 기본은 도넛 모양 그래프라고 하고, 해당 경우가 발견된다면 8자, 막대로 바꾸면 된다.
여기서 특징이 발견된다고 바로 return하지 말고 모든 정점을 순회하도록 한다.
왜냐하면 처음에 1번부터 n번까지 순회해서 아직 방문하지 않은 정점이라면 DFS 탐색을 하니까
미리 해당 부분 그래프의 모든 정점은 방문시켜서 또 다시 해당 그래프를 DFS하지 않도록 한다.
DFS,BFS 문제에서 많이 쓰던 테크닉이지..
1번부터 N번까지 순회해서 방문하지 않은 정점이면 DFS 탐색하는거
def dfs(u,graph,n,visited,in_edge,out_edge):
flag = True
stack = [u]
g = 1
while stack:
u = stack.pop()
if visited[u] == 1:
continue
visited[u] = 1
a = in_edge[u]
b = out_edge[u]
if a == 2 and b == 2:
g = 3
elif (a == 1 and b == 0) or (a == 0 and b == 1) or (a == 0 and b == 0):
g = 2
for v in graph[u]:
if visited[v] == 0:
stack.append(v)
return g,visited
여기서 1번부터 N번까지 순회해서 DFS를 할때 주의해야할 점은 막대모양 그래프인데
막대 모양 그래프를 온전히 순회할려면 '나가는 간선이 1개', '들어오는 간선이 0개'인 그래프에서 시작해야한다
그 외에 다른 정점에서 시작한다면 해당 부분 그래프의 모든 정점을 방문하지 못한다
우연히 1번부터 N번까지 순회하는데 시작 정점의 번호가 더 큰 경우가 당연히 있을 수 있다
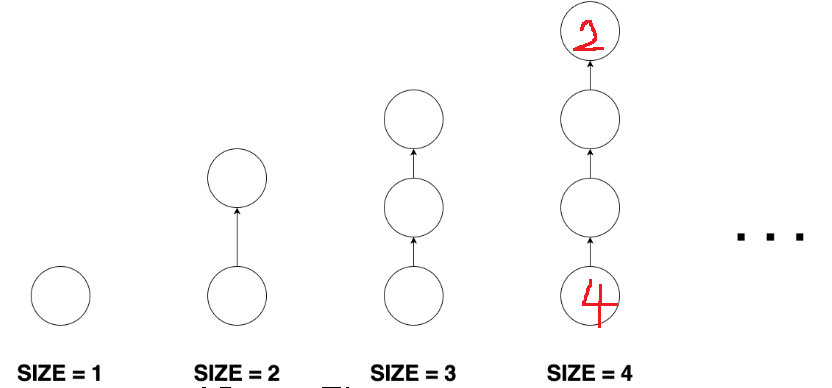
그래서 처음에는 이 막대 모양 그래프만을 찾기 위해.. 1번부터 N번까지 순회할때,
'아직 방문하지 않았고, 들어오는 간선이 0개, 나가는 간선이 1개'인 경우에만 DFS를 시작
그리고 나서 1번부터 N번까지 다시 순회해서 아직 방문하지 않은 정점인 경우에 DFS를 시작
visited = [0]*(n+1)
visited[start] = 1
for u in range(1,n+1):
if visited[u] == 0 and in_edge[u] == 0 and out_edge[u] == 1:
g,visited = dfs(u,graph,n,visited,in_edge,out_edge)
answer[g] += 1
for u in range(1,n+1):
if visited[u] == 0:
g,visited = dfs(u,graph,n,visited,in_edge,out_edge)
answer[g] += 1
이렇게 하면 시간안에 모든 부분 그래프를 순회할 수 있다.
기본에 충실하게 생각했다면.. 아쉽다
'무관한 정점'에서 나가는 간선을 삭제하고
굳이 삭제하는걸 생각 못했더라도...
"1번부터 N번까지 순회해서, 아직 방문하지 않은 정점이라면 DFS"
이 형태는 많이 한건데..
for u in range(1,n+1):
if visited[u] == 0:
g,visited = dfs(u,graph,n,visited,in_edge,out_edge)
answer[g] += 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------
공식적으로 제공된 애드혹같은 풀이는 훨씬 아름답다
각 정점이 가지는 들어오는 간선의 개수, 나가는 간선의 개수로 그래프가 어떤 모양인지 알 수 있다는 건 위에서 파악했는데
해당 부분 그래프 내에서 '들어오는 간선의 개수가 2개', '나가는 간선의 개수가 2개'인 정점을 하나 가지는 그래프는 8자모양
'들어오는 간선의 개수가 0개', '나가는 간선의 개수가 1개'인 정점 or
'들어오는 간선의 개수가 1개', '나가는 간선의 개수가 0개'인 정점 or
'들어오는 간선의 개수가 0개', '나가는 간선의 개수가 0개'인 정점이 있으면 막대 모양 그래프라는 걸 알 수 있었다.
1) 일단 각 정점이 가지는 들어오는 간선의 개수, 나가는 간선의 개수를 모두 세고
2) 1번부터 N번까지 순회해서 들어오는 간선의 개수가 0개, 나가는 간선의 개수가 2개 이상인 정점은 '생성된 무관한 정점'
3) '생성된 무관한 정점'과 연결된 간선을 모두 삭제
4) 이 때 연결된 간선의 개수가 평면 위 존재하는 그래프의 개수와 같다.
왜냐하면 정점에서 각 그래프의 정점 하나에 간선을 연결 시켰으니까
5) 다시 1번부터 N번까지 순회해서 '들어오는 간선의 개수가 2개', '나가는 간선의 개수가 2개'인 정점의 개수를 센다.
해당 정점 하나당 8자 모양 그래프이므로.. 이 개수가 8자 모양 그래프의 개수이다.
6) 그리고 '들어오는 간선의 개수가 0개'인 정점의 개수를 센다(혹은 '나가는 간선의 개수가 0개'인 정점)
'들어오는 간선의 개수가 0개'인 정점 하나당 막대 모양 그래프이므로, 이 개수가 막대 모양 그래프의 개수이다.
("하나의 정점은 하나의 부분 그래프 내에만 속한다는 사실을 생각해본다면...")
7) 평면 위 존재하는 총 그래프의 개수('생성된 무관한 정점'과 연결된 간선의 개수)
8자 모양, 막대 모양 그래프의 개수를 알고 있으므로 총 개수 - (8자 + 막대) = 도넛 모양 그래프의 개수이다.
def solution(edges):
answer = [0,0,0,0]
n = 0
graph = [[] for _ in range(1000001)]
in_edge = [0]*(1000001)
out_edge = [0]*(1000001)
for a,b in edges:
if n < a:
n = a
if n < b:
n = b
graph[a].append(b)
in_edge[b] += 1
out_edge[a] += 1
for i in range(1,n+1):
if in_edge[i] == 0 and out_edge[i] >= 2:
start = i
break
answer[0] = start
total = 0
for v in graph[start]:
total += 1
in_edge[v] -= 1
for u in range(1,n+1):
if u == start:
continue
if in_edge[u] == 0:
answer[2] += 1
if in_edge[u] == 2 and out_edge[u] == 2:
answer[3] += 1
answer[1] = total - (answer[2] + answer[3])
return answer'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 무방향 연결그래프에서 정점의 성질 관찰하기 (0) | 2024.05.10 |
|---|---|
| ABC 351 F번 복기 - 알고리즘 문제에 max함수를 바꾸는 트릭 2가지 (0) | 2024.05.02 |
| XOR 문제에 접근하기 위해 반드시 필요한 스킬3 -모든 쌍의 XOR의 합(sum of all pair of xor)- (0) | 2024.01.27 |
| XOR 문제에 접근하기 위해 반드시 필요한 스킬2 - 연속하는 부분열의 XOR- (0) | 2024.01.25 |
| XOR 문제에 접근하기 위해 반드시 필요한 스킬1 - 기본 성질 - (0) | 2024.01.23 |

