1. 연속하는 부분열에 대한 XOR
n개의 음이 아닌 정수 $A_{1}, A_{2}, ... , A_{n}$에 대하여 L번부터 R번까지의 XOR
$A_{L} \oplus A_{L+1} \oplus ... A_{R}$의 값은?
만약 $V_{0} = 0, V_{i} = A_{1} \oplus A_{2} \oplus ... \oplus A_{i}$라고 하자.
$V_{L-1} = A_{1} \oplus A_{2} \oplus A_{3} .... \oplus A_{L-1}$이다.
그러면, $0 \oplus x = x, x \oplus x = 0$이므로.. 0을 xor해도 값이 달라지지 않는다.
$$A_{L} \oplus A_{L+1} \oplus ... A_{R} = 0 \oplus (A_{L} \oplus A_{L+1} \oplus ... A_{R})$$
그런데 $0 = V_{L-1} \oplus V_{L-1}$이므로... 결합법칙을 이용해서 다음과 같이 바꾼다
$$V_{L-1} \oplus V_{L-1} \oplus (A_{L} \oplus ... A_{R}) = V_{L-1} \oplus (V_{L-1} \oplus A_{L} ... A_{R})$$
그런데 $V_{L-1} \oplus A_{L} ... A_{R} = A_{1} \oplus A_{2} ... A_{L-1} \oplus A_{L} ... A_{R}$이다.
즉, 1번부터 R번까지의 XOR과 같다.
따라서, $$A_{L} \oplus A_{L+1} \oplus ... \oplus A_{R} = V_{L-1} \oplus V_{R}$$
누적합을 구하듯이 $V_{i}$를 모두 구해놓는다면 L번부터 R번까지의 연속하는 XOR은 $V_{L-1}$과 $V_{R}$의 XOR로 바로 구할 수 있다.
특히 교환법칙이 성립하므로 $V_{R}$과 $V_{L-1}$의 XOR로 구해도 된다는 점에 주목한다
2. 연습문제
10464번: XOR
입력의 첫 번째 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 1000)가 주어진다. 다음 T 개의 줄에는 두 개의 정수 S와 F가 주어진다. (1 ≤ S ≤ F ≤ 1 000 000 000)
www.acmicpc.net
3. 풀이
S에서 F까지 연속하는 모든 정수의 XOR을 구해야한다.
S부터 F까지 XOR해서 구할 수도 있겠지만 테스트 케이스가 1000개나 주어지고 F의 최대가 1000000000이니
단순하게하면 1초안에 1부터 1000000000까지 순회하는데도 시간초과
그래서 다음과 같은 사실을 관찰해야한다.
1부터 n까지 n = 1,2,3,..부터 XOR을 해본다면.. n이 4의 배수에는 XOR값이 n과 같아진다.
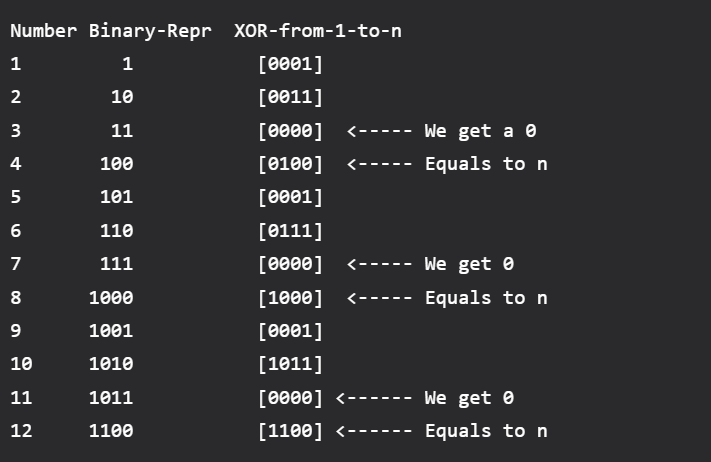
그리고 n이 4로 나눈 나머지가 1이면.. 1부터 n까지 xor값은 1이다.
왜냐하면 n이 4로 나눈 나머지가 0일때 1부터 n까지 xor 값이 n이고... 여기서 n+1과 xor한 것과 같은데
n과 n+1은 2진수 표현에서 맨 오른쪽 비트만 빼고 전부 같기 때문이다.
n : ?????...0
n+1: ?????...1
그리고 n이 4로 나눈 나머지가 2이면?
1부터 n-1까지 xor한 값은.. n-1은 4로 나눈 나머지가 1이므로 1이라는 사실을 알 수 있다.
그리고 1에 n을 xor한 값을 구해야하는데 n의 2진수 표현에는 맨 오른쪽 비트가 0이어야한다.
왜냐하면 n을 4로 나눈 나머지가 2이기 때문에
따라서 1부터 n까지 xor하면 n+1이 된다.
마지막으로 n이 4로 나눈 나머지가 3이면?
1부터 n-1까지 xor하면 n-1은 4로 나눈 나머지가 2이므로 n이 된다.
따라서 1부터 n까지 xor한 값은 n과 n의 xor과 같으므로 무조건 0이다.
사실 1부터 4까지 xor했을 때 4가 나온다는 사실이 일단 중요하다.
그리고 5,6,7까지 각각 xor했을때 어떤 값이 나오는지 확인해본다.
1부터 5까지 xor은 4와 5의 xor이고 이는 4와 5의 맨 오른쪽 비트만 차이 있으므로 1이다.
1부터 6까지의 xor은 1과 6의 xor이다. 6은 맨 오른쪽 비트가 0이니 6+1 = 7이다.
1부터 7까지의 xor은 7과 7의 xor이다. 같은 수 끼리 xor했으니 0이다.
그리고 8까지의 xor이 8이 나오고 위의 논리를 반복적용하면 1부터 n까지 xor을 일반화할 수 있다.
----------------------------------------------------------------------------------------------------------------------------------
s,f가 주어질때 1부터 s-1까지의 xor, 1부터 r까지의 xor을 각각 구하고
두 값의 xor을 구하면 끝
1부터 n까지의 xor은 n을 4로 나눈 나머지에 따라 n,1,n+1,0이라는 사실을 이용
from sys import stdin
def value(i):
r = i % 4
if r == 0:
return i
elif r == 1:
return 1
elif r == 2:
return i+1
else:
return 0
T = int(stdin.readline())
for _ in range(T):
s,f = map(int,stdin.readline().split())
v1 = value(s-1)
v2 = value(f)
print(v1 ^ v2)
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 코딩테스트 복기 - 복잡한 그래프 생각하면서 효율적으로 탐색 하기 (0) | 2024.02.03 |
|---|---|
| XOR 문제에 접근하기 위해 반드시 필요한 스킬3 -모든 쌍의 XOR의 합(sum of all pair of xor)- (0) | 2024.01.27 |
| XOR 문제에 접근하기 위해 반드시 필요한 스킬1 - 기본 성질 - (0) | 2024.01.23 |
| ABC 334 복기 - 배열에서 원소 하나를 제거해서 두 원소 절댓값 차이의 합을 최소로 만들기(prefix sum, suffix sum) (0) | 2024.01.01 |
| 의외로 알아내기 어려운 2의 거듭제곱을 더하면 나타나는 특징 (0) | 2023.10.09 |

