18668번: Find the Vertex (acmicpc.net)
무방향 연결그래프가 주어지고, self-loop나 multiple edge가 없다.
정점의 번호가 1번부터 n번까지 되어있고, 시작정점 s번에서 다른 정점까지의 거리를 3으로 나눈 나머지가 배열로 주어진다.
여기서 s가 무엇인지 찾는 문제
n,m 제한이 50만이다보니, 하나하나 해보기는 어렵다.
일단 거리 배열에서 0인 값인 정점 번호가 일단 정답 후보가 될 것이다.
시작정점 s에서 거리가 3,6,9,... 3의 배수여도 0이기 때문에 정답이 아닌 정점이 있을 수도 있다.
또 하나 알 수 있는 점은, 시작정점 s라면 인접한 정점까지 거리는 무조건 1이다.

물론 위 그림과 같이 s에서 인접한 3개 정점과 똑같이 인접한 어떤 정점 A가 존재할 수 있는데...
그 A는 d값이 0일 수 없다.
조건에 따라 s가 여러개일 수는 있지만, 어쨌든 시작 정점 s는 하나여야한다.
s에서 출발해서 다른 정점까지 거리가 주어진거니까
그래서 s가 0이면 A는 2여야하고, A가 0이면 s는 2여야한다.
물론 s, A가 모두 0일 수 있는데 그러한 경우는..?
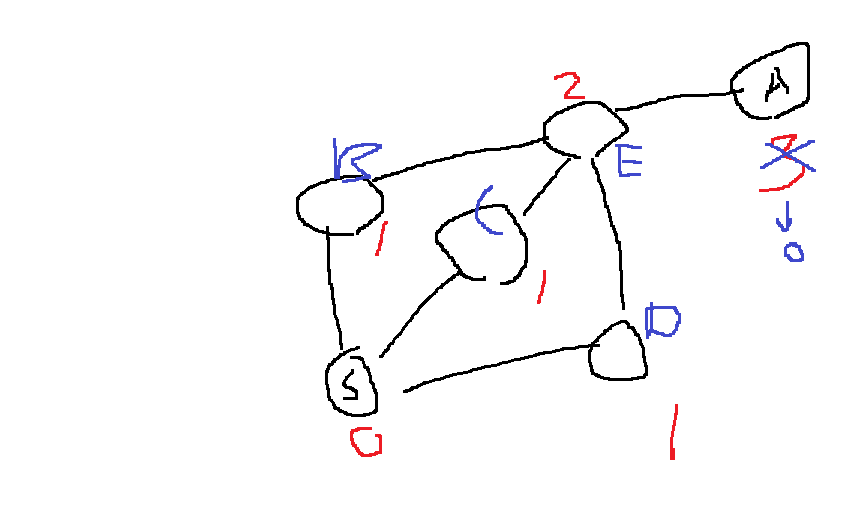
위와 같이 A는 무조건 s와 인접한 3개 정점 B,C,D와의 거리가 2이상이 된다
따라서 시작 정점이라면 거리 d값이 0이어야하고, 시작 정점에서 인접한 정점과는 모두 1이어야하며 이러한 정점이 유일하다.
from sys import stdin
n,m = map(int,stdin.readline().split())
d = list(map(int,stdin.readline().split()))
graph = [[] for _ in range(n+1)]
for _ in range(m):
a,b = map(int,stdin.readline().split())
graph[a].append(b)
graph[b].append(a)
s = []
for i in range(n):
if d[i] == 0:
s.append(i+1)
for u in s:
no = False
for v in graph[u]:
if d[v-1] != 1:
no = True
break
if no == False:
print(u)
break728x90
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 배열을 뒤집었을때 생기는 반전 수의 개수 구하기 (0) | 2024.05.23 |
|---|---|
| 정수들이 섞여있는 수열에서 연속하는 정수 수열을 O(N)에 분리하기 (0) | 2024.05.12 |
| ABC 351 F번 복기 - 알고리즘 문제에 max함수를 바꾸는 트릭 2가지 (0) | 2024.05.02 |
| 코딩테스트 복기 - 복잡한 그래프 생각하면서 효율적으로 탐색 하기 (0) | 2024.02.03 |
| XOR 문제에 접근하기 위해 반드시 필요한 스킬3 -모든 쌍의 XOR의 합(sum of all pair of xor)- (0) | 2024.01.27 |

